Exercícios de Lei da Refração - Lista de Exercícios Resolvida
Questão 1
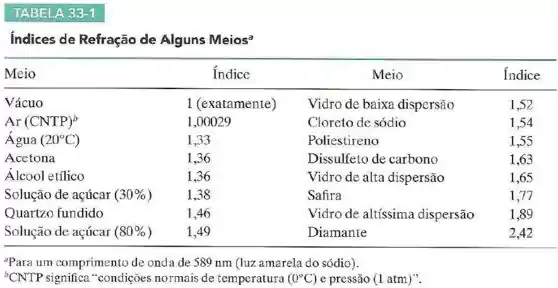
Qual é a diferença, em metros por segundo, entre a velocidade da luz na safira e a velocidade da luz no diamante?
Veja a Tabela 33-1.
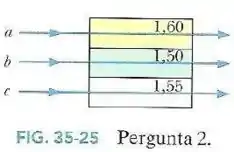
Questão 2
Um raio de luz incide sobre a superfície plana que separa duas placas finas de vidro com índices de refração e .
O ângulo de incidência é , e o raio que provém da placa que possui índice de refração .
Calcule o ângulo de refração.
Ver solução completaQuestão 3
Na Fig.35-25 três pulsos luminosos de mesmo comprimento de onda, , e , atravessam blocos de plásticos de mesmo comprimento cujos índices de refração são dados.
Coloque os pulsos na ordem do tempo que levam para atravessar os blocos, começando pelo mais lento.
Questão 4
Na Fig.33-53 uma estaca vertical com de comprimento se projeta do fundo de uma piscina até um ponto acima da água. O sol está acima do horizonte.
Qual é o comprimento da sombra da estaca no fundo da piscina?
O índice de refração da água é de .

Questão 5
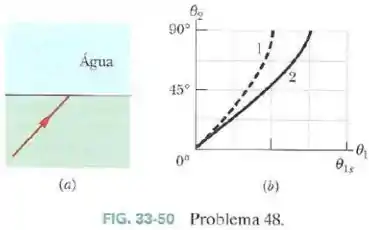
Na Fig.33-50a um raio luminoso que está se propagando inicialmente em um certo material incide com um ângulo na água, onde parte da luz se refrata. O outro material pode ser do tipo ou do tipo ; a FIg.33-50b mostra o ângulo de refração em função do ângulo de incidência para os dois tipos de material.
A escala do eixo horizontal é definida por . Sem fazer nenhum cálculo, determine:
- Se o índice de refração do material é maior ou menor que o índice de refração da água ().
- Se o índice de refração do material é maior ou menor que o índice de refração da água.
- Do material .
- Do material .
Determine o índice de refração:
Questão 6
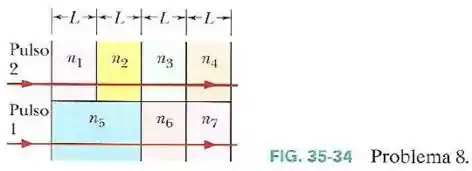
Na Fig.35-34, dois pulsos luminosos atravessam placas de plástico de espessura ou e índices de refração , , , , , e .
- Qual dos dois pulsos chega primeiro à outra extremidade das placas?
- A diferença entre os tempos de trânsito dos dois pulsos é igual a que múltiplo de ?
Questão 7
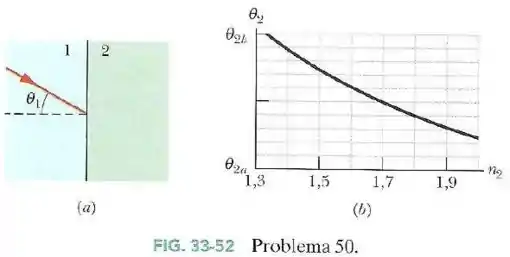
Na Fig.33-52a um feixe luminoso que está se propagando inicialmente no material incide no material com um ângulo de . A refração da luz no material depende, entre outros fatores, do índice de refração do material .
A Fig.33-52b mostra o ângulo de refração em função de . A escala do eixo vertical é definida por e .
- Qual é o índice de refração do material ?
- Se o ângulo de incidência aumenta para e , qual é o valor de ?
Questão 8
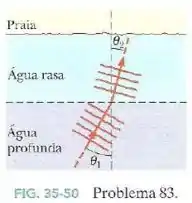
Ondas oceânicas, com uma velocidade de , se aproximam da praia fazendo um ângulo de com a normal, como se vê na vista de topo da Fig.35-50. A profundidade da água muda bruscamente a uma certa distância da praia, fazendo a velocidade das ondas diminuir para .
- Qual é o ângulo entre a direção das ondas e a normal perto da praia? (Suponha que a lei de refração é a mesma que para a luz)
- Explique por que quase sempre as ondas incidem perpendicularmente à praia, mesmo quando se aproximam da costa fazendo um ângulo relativamente grande com a normal.
Questão 9
Um feixe de luz desloca-se no quartzo com velocidade . O comprimento de onda da luz no quartzo é .
- Qual é o índice de refração do quartzo para esse comprimento de onda?
- Se essa mesma luz se propagasse no ar, qual seria seu comprimento de onda?
Questão 10
Um raio de luz que se propaga no ar incide sobre a superfície de um bloco de plástico em um ângulo de com a normal e se desvia até formar um ângulo de com a normal no plástico.
Calcule a velocidade da luz no plástico.
Ver solução completaQuestão 11
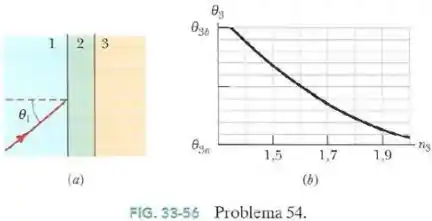
Na Fig.33-56a um feixe de luz que estava se propagando no material incide com um ângulo na interface com o material . Parte da luz penetra no material e parte dessa luz penetra no material ; todas as interfaces são paralelas.
A orientação do feixe no material depende em parte do índice de refração do terceiro material. A Fig.33-56b mostra o ângulo em função de .
A escala do eixo vertical é definida por e .
- É possível calcular o índice de refração do material com base nessas informações? Se a resposta for afirmativa, determine o valor de .
- É possível calcular o índice de refração do material com base nessas informações? Se a resposta for afirmativa, determine o valor de .
- Se e , qual é o valor de ?
Questão 12
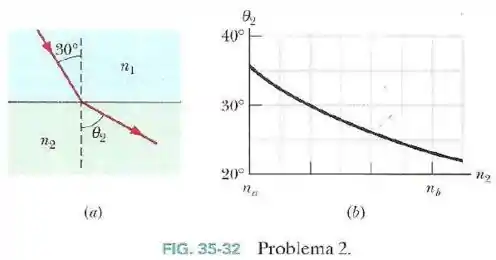
Na Fig.35-32a, um raio luminoso que estava se propagando no material incide em uma interface com um ângulo de . O desvio sofrido pelo raio devido à refração depende, em parte, do índice de refração do material .
A Fig.35-32b mostra o ângulo de refração em função de . A escala do eixo horizontal é definida por e .
Qual é a velocidade da luz no material ?
Questão 13
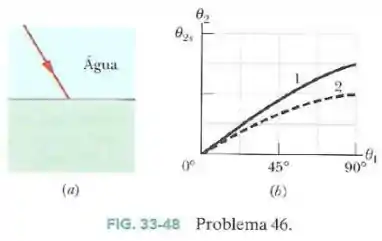
Na Fig.33-48a um raio luminoso que está se propagando inicialmente na água incide com um ângulo em outro material, no qual parte da luz se refrata. O outro material pode ser do tipo ou do tipo ; a Fig.33-48b mostra o ângulo de refração em função do ângulo de incidência para os dois tipos de material.
A escala do eixo vertical é definida por . Sem fazer nenhum cálculo, determine:
- Se o índice de refração do material é maior ou menor que o índice de refração da água ()
- Se o índice de refração do material é maior ou menor que o índice de refração da água.
- Do material .
- Do material .
Determine o índice de refração:
Questão 14
O comprimento de onda da luz amarela do sódio no ar é .
- Qual é a frequência da luz?
- Qual é o comprimento de onda da luz em um vidro com um índice de refração de ?
- Use os resultados dos itens (a) e (b) para calcular a velocidade da luz no vidro.
Questão 15
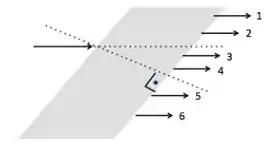
A figura abaixo ilustra um raio policromático incidindo na superfície de um paralelepípedo (a reta normal á superfície de incidência está indicada na figura).
O índice de refração do ar é e o índice de refração do paralelepípedo é função da frequência, maior que para toda frequência e satisfaz .
Sendo as frequências dos raios , respectivamente, podemos afirmar que
- e os raios , , e não existem.
- e os raios , , e não existem.
- e os raios , , e não existem.
- e os raios , , e não existem.
- e os raios , , e não existem.
- e os raios , , e não existem.
Questão 16
Um raio de luz monocromático (frequência única, comprimento de onda único) no ar () entra em um prisma de vidro (). No prisma de vidro
A) tanto a frequência como o comprimento de onda são os mesmos que no ar
B) a frequência é a mesma, mas o comprimento de onda é maior que no ar
C) a frequência é a mesma, mas o comprimento de onda é menor que no ar
D) o comprimento de onda é o mesmo, mas a frequência é maior que no ar
E) o comprimento de onda é o mesmo, mas a frequência é menor que no ar
Ver solução completaQuestão 17
Considere as seguintes afirmações.
- James C. Maxwell introduziu o termo conhecido por densidade de corrente de deslocamento nas equações do eletromagnetismo.
- As equações do eletromagnetismo que eram aceitas antes de James C. Maxwell explicavam as ondas eletromagnéticas, porém, a velocidade de propagação prevista não estava de acordo com os dados experimentais.
- Pelas equações de Maxwell para o eletromagnetismo, quanto maior o índice de refração de um meio material, menor é a velocidade de propagação da luz nesse meio.
- Apenas é verdadeira.
- Apenas é verdadeira.
- Apenas é verdadeira.
- Apenas e são verdadeiras
- Apenas e são verdadeiras.
- Apenas e são verdadeiras.
- Todas as afirmativas são verdadeiras.
- Nenhuma afirmativa é verdadeira.
Questão 18
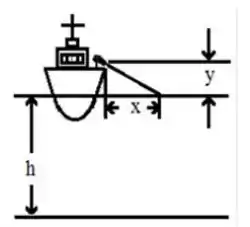
A figura, um laser posicionado sobre um navio é utilizado para comunicar-se com um pequeno submarino de pesquisa com duas pessoas, assentado no fundo de um lago. O laser está posicionado a m da superfície do lago e incide na água a m a partir da lateral do navio. O submarino está a uma profundidade , e a água tem um índice de refração igual a . Qual é a distância horizontal d do submarino, a partir da lateral do navio?
A)
B)
C)
D)
E)
Ver solução completaQuestão 19
É conhecido que um campo elétrico de uma onda plana eletromagnética propagando-se num meio dielétrico (onde ) é dado por
onde , e .
Obs: As relações e as equações para uma onda eletromagnética num meio dielétrico são as mesmas que para uma onda eletromagnética no vácuo, substituindo apenas nas relações a velocidade da onda eletromagnética no vácuo pela velocidade da onda eletromagnética no meio dielétrico.
Qual é o índice de refração do meio?
Qual é o vetor unitário da direção propagação da onda?
Calcule o vetor campo magnético da onda.
Que tipo de polarização tem esta onda? Justifique a sua resposta.
Determine o vetor de Poynting .
Ver solução completaQuestão 20
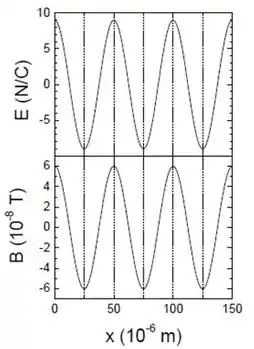
Uma onda eletromagnética plana e monocromática propaga-se num meio material com permeabilidade magnética igual a .
No instante , os campos elétrico e magnético são descritos por e , onde e são funções de apresentadas na figura abaixo.
São dados:
e
- Qual é a direção de propagação dessa onda? Justifique.
- Quais são a velocidade dessa onda e o índice de refração do meio?
- Qual é o valor da permissividade desse meio?
- Qual é a frequência dessa onda?
- Em relação a esta onda, qual é a média temporal da energia contida num volume correspondente a um metro cúbico?
Questão 21
Uma pessoa enxerga uma lâmpada no fundo de uma piscina através de raios luminoso próximos da normal. Ele estima a profundidade da piscina em . Do lado da piscina, existe um alerta para crianças, indicando a profundidade real de .
A discrepância entre a estimativa da pessoa e o valor correto é devido à profundidade aparente ocasionada pela refração da luz.
Utilizando a aproximação de pequenos ângulos para os ângulos dos feixes incidente e refratado, determine o índice de refração do líquido da piscina.
- 1,4
- 1,6
- 1,8
- 2,0
- 2,2
Questão 22
Ao atravessas a barreira entre o vácuo do espaço para a atmosfera terrestre (), um raio de luz solar tem sua velocidade alterada de para
Questão 23
Um banhista olha para dentro de uma piscina em uma parte com profundidade real de . O índice de refração da água da piscina é aproximado por .
Utilizando a aproximação de pequenos ângulos para os feixes incidente e refratado, estime a profundidade aparente da piscina observada pelo banhista.
Questão 24
Considere as seguintes afirmações sobre a passagem de um raio luminoso do vácuo para um meio transparente, homogêneo e linear:
- A velocidade do raio luminoso permanece inalterada
- A frequência do raio luminoso permanece inalterada
- O comprimento de onda do raio luminoso aumenta.
Determine o item CORRETO.
- Apenas e estão corretas.
- Apenas está correta.
- Todas estão corretas.
- Nenhuma está correta.
- Apenas e estão corretas.
- Apenas está correta.
Questão 25
Um raio de luz atinge um cristal de gelo hexagonal flutuando no ar em um ângulo de com a face mais à esquerda, como mostrado na figura abaixo. O cristal tem a forma de um prisma hexagonal. Todos os raios mostrados estão no plano da página e . Qual raio de saída é o correto?
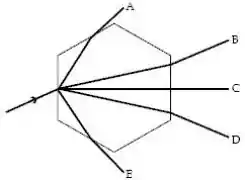
A) A
B) B
C) C
D) D
E) E
Ver solução completaQuestão 26
Quando a luz passa do ar para a água:
A) sua velocidade, comprimento de onda e freqüência mudam.
B) sua velocidade muda, mas sua freqüência e comprimento de onda não mudam.
C) sua freqüência muda, mas sua velocidade e comprimento de onda não mudam.
D) sua velocidade e comprimento de onda mudam, mas sua freqüência não muda.
E) seu comprimento de onda muda, mas sua velocidade e freqüência não mudam.
Ver solução completaQuestão 27
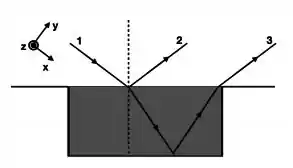
Enunciado Um feixe de luz monocromática, bem colimado e de pequeno diâmetro, propaga-se no ar e atinge a interface de uma piscina com água (n = 1,33), de profundidade 1,6m. Considere que esse feixe é emitido a partir de uma altura de 40 cm em relação à superfície da água, fazendo um ângulo de 45° com a normal à superfície.
(a) Parte do feixe penetra na água, reflete no fundo da piscina e volta ao ar (ver figura).
Qual é o caminho ótico percorrido por este feixe entre os pontos 1 e 3, estando o
ponto 3 à mesma altura do ponto 1?
Ver solução completaQuestão 28
Considere as sentenças a seguir sobre a reflexão e refração da luz com dois meios materiais diferentes: I) os comprimentos de onda dos raios incidente, refletido e refratado são idênticos; II) o módulo da velocidade de propagação dos raios incidente, refletido e refratado são idênticos; e III) as frequências dos raios incidente, refletido e refratado são idênticas. Marque a opção correta
(a) nenhuma é verdadeira.
(b) apenas I é verdadeira.
(c) apenas I e III são verdadeiras.
(d) apenas II é verdadeira.
(e) apenas I e II são verdadeiras.
(f) apenas III é verdadeira.
(g) apenas II e III são verdadeiras.
Ver solução completaQuestão 29
Um feixe de luz monocromático parte do vácuo e incide em um determinado material com um ângulo de incidência de .
O ângulo formado entre a direção do feixe incidente e a direção do feixe refratado é de .
Determine o índice de refração do material.
Questão 30
Alguns escritores e músicos tiveram em seus textos e canções a física como inspiração. Antonio Carlos Jobim, nosso maestro soberano, autor de diversas canções, inspirou -se em alguns conceitos da óptica par a escrever um trecho da linda canção Luiza. Leia atentamente as palavras de Tom Jobim e assinale a alternativa correta:
"O teu desejo é sempre o m eu desejo
Vem, me exorciza
Dá-me tua boca
E a rosa louca
Vem me dar um beijo
E um raio de sol
Nos teus cabelos
Como um brilhante que partindo a luz
Explode em sete cores
Revelando ent o os sete mil amor es
Que eu guardei somente pra te dar Luiza"
- O que explica a decomposição da luz nas sete cores, cantada por Tom Jobim, é o fato da luz branca poder ser decomposta em 7 comprimentos de onda ao passar por meios com índices de refração diferentes.
- Para que a decomposição da luz ocorra é necessário que a fonte luminosa utilizada seja monocromática.
- A refração e a reflexão luminosa ocorrem apenas quando utilizamos fontes de luz monocromáticas.
- A luz branca, em hipótese alguma sofre decomposição em cores diferentes que são representadas por 7 comprimentos de onda.
- Tom Jobim acertou ao descrever a decomposição da luz branca visto que porque esse fenômeno ocorre devido a reflexão da luz ao passar por meios com índices de refração diferentes.