Enunciado
Física - Young and Freedman - Vol 4- Ed: 12º - Capítulo 33.Problemas - Ex. 46
Depois de passar o dia dirigindo, ao anoitecer você vai nadar na piscina do hotel. Ao voltar para o quarto, você nota que perdeu a chave da porta na piscina. Você pede emprestada uma lanterna e começa a procurar a chave percorrendo a borda da piscina e fazendo a luz incidir sobre a água. A luz brilha ao incidir na chave que está no fundo da piscina quando a lanterna está a acima da superfície da água e o ponto de incidência da luz está a uma distância de da beira da piscina (Figura 33.47). Sabendo que a profundidade da água no fundo da piscina é de , qual é a distância entre a chave e a beira da piscina?
Passo 1
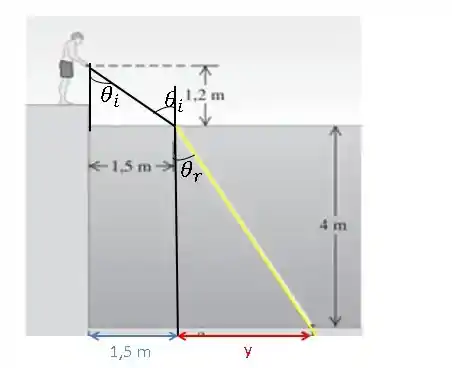
Vamos fazer um desenho para ajudar a entender o que está acontecendo.
Coloquei os ângulo de incidência e de refração ali na interface entre ar e água. E também marquei a distância y ali. Na verdade o exercício pediu . Então vamos achar o y e depois achamos o x, ok?
Passo 2
Vamos aplicar a lei de snell na interface ar-agua:
Sabemos que:
Mas não sabemos os ângulos. Então vamos olhar lá para o desenho do passo 1.
Primeiro, o triângulo retângulo formado com o . Temos:
Beleza! Agora falta o . Então, voltando para a lei de snell:
Resolvendo isso, encontramos:
Show! O exercício pede a distância x. Para isso, temos que achar y. Então vamos lá
Olhando para o segundo triângulo retângulo, temos:
Mas,
Maravilha! Agora ficou moleza!