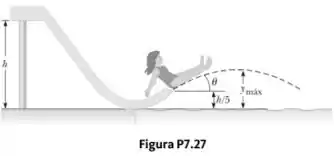
. Uma criança de massa começa do repouso e desliza sem atrito de uma altura h ao longo de um escorregador ao lado de uma piscina (Fig. P). Ela é lançada de uma altura no ar acima da piscina. Queremos encontrar a altura máxima que ela atinge acima da água em seu movimento de projétil. O sistema criança-Terra é isolado ou não isolado? Por quê? Há

uma força não conservativa atuando dentro do sistema? Defina a configuração do sistema quando a criança está no nível da água como tendo energia potencial gravitacional zero. Expresse a energia total do sistema quando a criança está no topo do escorregador. Expresse a energia total do sistema quando a criança está no ponto de lançamento. Expresse a energia total do sistema quando a criança está no ponto máximo de seu movimento de projétil. Com base nas partes e , determine sua velocidade inicial no ponto de lançamento em termos de e . Com base nas partes e , determine sua altura máxima no ar em termos de e o ângulo de lançamento .

Suas respostas seriam as mesmas se o escorregador tivesse atrito? Explique.

Vamos começar com o item .

Para saber se o sistema criança -Terra é isolado, temos que ver se há alguma força que cause dissipação de energia.

Como a criança desliza sem atrito, ela não perde energia por conta disso e a única força atuando nela é a gravitacional, logo esse sistema é fechado.

Agora vamos para o item .

A única força na situação da criança no toboágua que poderia dissipar energia, com isso não conservativa, seria de atrito, mas como não temos atrito na situação não temos força dissipativa.

Vamos para o item

A energia total desse sistema é dada pela soma da energia cinética e da energia potencial, logo:

Mas como no topo a criança está em repouso, ela não vai ter energia cinética e toda sua energia vai ser potencial com , assim:

Agora vamos para o item .

Agora ele quer a energia total no ponto de lançamento. Nessa posição a criança vai ter uma velocidade que vamos chamar de que vai ser a velocidade com que ela sai da rampa e ela vai ter uma altura . Com isso temos que:

Agora vamos para o item .

Quando a criança sai do toboágua ela se comporta como um projétil lançado, então ela tem componentes de velocidade na direção e , só que no ponto máximo de seu lançamento, ela só tem velocidade na direção .

Então só precisamos levar em conta a velocidade para escrever a expressão da energia nesse ponto, assim:

Agora vamos para o item .

No nosso sistema a energia total se conserva, então a energia no topo do toboágua é igual a energia total no ponto de lançamento, assim:

Agora temos que isolar , assim:

Então temos que:

Agora vamos para o item .

Agora temos que ir atrás da altura máxima , vamos usar a conservação de energia mais uma vez só que agora entre a energia total do ponto de lançamento e o ponto onde temos altura máxima.

Com isso temos que:

Em um lançamento obliquo a velocidade na direção é constante, logo:

Assim temos:

Substituindo a expressão que temos para , temos:

Dividindo tudo por :

Agora usando que , temos:

Finalmente o último, o item .

O atrito é uma força não conservativa, então a energia não iria conserva, então a gente teria que analisar as situações de forma diferente para encontrar o que ele pedia, logo as respostas seriam diferentes.