Exercícios de Conservação da Energia Mecânica - Lista de Exercícios Resolvida
Questão 1
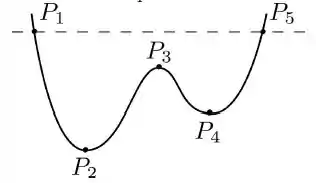
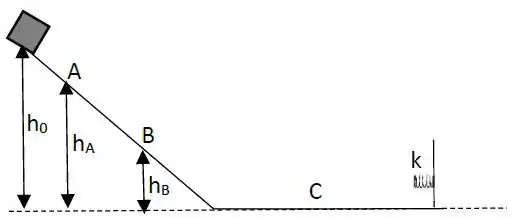
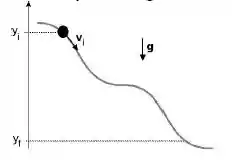
Um pequeno bloco, inicialmente em repouso, é liberado em uma rampa sem atrito a uma altura de . As alturas das elevações ao longo da rampa estão indicadas na figura. Os cumes das elevações são todos iguais, de forma circular, e o bloco não perde contato com o piso em nenhuma das elevações.
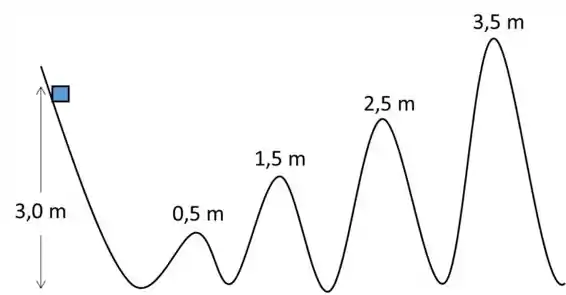
Qual é a primeira elevação que o bloco não consegue superar?
O que acontece com o bloco em seguida?
Ver solução completaQuestão 2
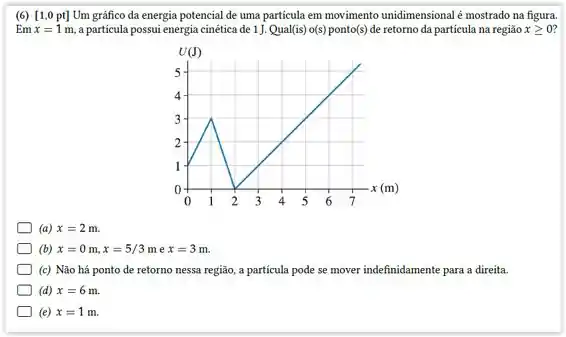
Uma máquina de Atwood consiste em duas massas, e e uma polia sem massa e sem atrito. Partindo do repouso, a rapidez das duas massas chega ao final de . Neste tempo, a energia cinética do sistema atinge e cada massa terá se deslocado uma distância de . Determine os valores de e .

Questão 3
Uma massa está suspensa no campo gravitacional por uma mola de constante elástica presa ao teto. Efeitos de atrito são desprezíveis e observa-se que o sistema oscila verticalmente em torno de sua posição de equilíbrio. A opção correta é:
- A energia mecânica do sistema não se conserva, pois alem da força gravitacional sobre a massa há, adicionalmente, a força elástica exercida pela mola.
- A energia mecânica do sistema se conserva, se considerarmos que esta é a soma das energias cinética e energia potencial gravitacional da massa.
- A energia mecânica do sistema se conserva, se considerarmos que esta é a soma das energias cinéticas e energia potencial elástica da mola.
- A energia potencial total, dada como a soma das contribuições de energia potencial gravitacional e energia potencial elástica, é conservada.
- A energia mecânica do sistema se conserva, se considerarmos que esta é a soma das energias cinética e das energias potencial gravitacional e potencial elástica da mola.
Questão 4
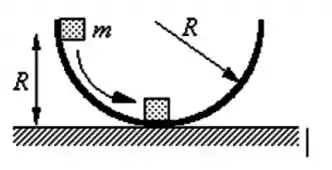
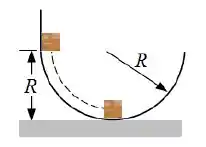
Um carrinho de montanha-russa, de , parte do repouso de uma altura acima da base de uma laço de de diâmetro. Se o atrito é desprezível, determine a força para baixo exercida pelos trilhos sobre o carrinho, quando este está no topo do laço, de cabeça para baixo.

Questão 5
Um bloco de desliza sobre uma superfície horizontal sem atrito com uma rapidez de . Após deslizar por uma distância de , o bloco faz uma suave transição para uma rampa sem atrito inclinada de um ângulo de com a horizontal. Qual a distância, ao longo da rampa, que o bloco percorre até atingir momentanaeamente o repouso? ()

Questão 6
Um corpo de massa é abandonado do alto de um plano inclinado (1), que possui altura em relação ao solo, e percorre seu comprimento livre de forças de atrito até entrar em um movimento de “loop” (2), conforme mostra a figura. Use para a aceleração da gravidade.
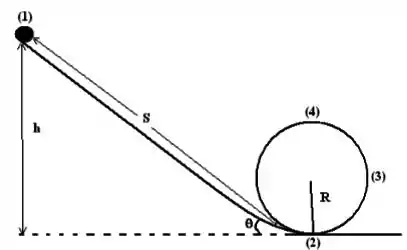
a) Utilizando um eixo de coordenadas com a direção paralela ao plano inclinado, represente o diagrama de corpo livre para a situação na qual o corpo se encontra na posição (1) e descreva, a partir da segunda lei de Newton, as componentes das forças que atuam no corpo para cada eixo.
b) Escreva a expressão para a velocidade em função da altura de lanamento com que o corpo chega à posição (2) indicada na figura.
c) Escreva a segunda lei de Newton por componentes para a situação na qual o corpo se encontra na posição (4) com velocidade e obtenha uma expressão para a altura mínima , em função do raio , de onde o corpo deve ser lançado para que consiga completar a volta no loop.
d) Considerando que o corpo abandonado de uma altura e o loop tem um raio , sua velocidade no ponto (3) é . Calcule os módulos e direções da força normal e da força resultante que atuam no corpo ao passar naquele ponto. Use .
Ver solução completaQuestão 7
Engenheiros projetam um sistema por meio do qual uma massa em queda livre imprime energia cinética a um tambor uniforme em rotação, ao qual a massa está presa por um cabo delgado e leve, enrolado em volta do tambor (figura abaixo). Não há nenhum atrito significativo no eixo do tambor e tudo parte do repouso. Esse sistema está sendo testado na Terra, mas é para ser usado em Marte, onde a aceleração da gravidade é . Nos testes na Terra, quando m possui e deve cair por , ela fornece de energia cinética ao tambor.
a) Quando o sistema for operado em Marte, qual a distância a massa de terá que cair para gerar o mesmo valor de energia cinética para o tambor?
Ver solução completaQuestão 8
Um sistema massa-mola horizontal executa um movimento harmônico simples com amplitude . Quando o deslocamento da massa é , qual das expressões abaixo representa corretamente a rapidez da massa em termos de sua rapidez máxima? Dica: use a conservação da energia.
(A) (B)(C) (D)v=3 (E)
Ver solução completaQuestão 9
Engenheiros projetam um sistema por meio do qual uma massa em queda livre imprime energia cinética a um tambor uniforme em rotação, ao qual a massa está presa por um cabo delgado e leve, enrolado em volta do tambor (figura abaixo). Não há nenhum atrito significativo no eixo do tambor e tudo parte do repouso. Esse sistema está sendo testado na Terra, mas é para ser usado em Marte, onde a aceleração da gravidade é . Nos testes na Terra, quando m possui e deve cair por , ela fornece de energia cinética ao tambor.
b) Qual a velocidade da massa de em Marte quando o tambor obtiver de energia cinética?
Ver solução completaQuestão 10
Um pássaro de está voando horizontalmente a, quando inadvertidamente colide com uma barra vertical fixa, atingindo a abaixo do topo (ver figura abaixo). A barra homogênea com de comprimento e massa de está presa por uma dobradiça na sua base. A colisão atordoa o pássaro que cai ao chão em seguida. Qual é a velocidade angular da barra a) logo após ser atingida pelo pássaro e b) assim que atinge o solo?
Ver solução completaQuestão 11
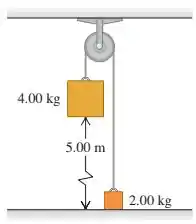
Uma polia indicada na figura abaixo possui raio e momento de inércia de . A corda não desliza sobre a periferia da polia. Use métodos de conservação da energia para calcular a velocidade do bloco de no momento em que ele atinge o solo.
Questão 12
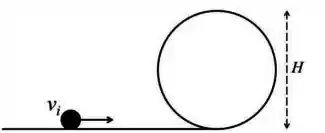
Um corpo puntiforme de massa e velocidade inicial se desloca sobre uma superfície horizontal sem atrito. Ao final dessa superfície existe um “loop” circular de diâmetro . Assumindo que não há atrito durante o “loop”, para que o corpo o complete, o módulo da velocidade deve ser tal que:
Questão 13
Num parque de diversões, um carrinho desce sem atrito de uma altura para dar a volta num loop circular de raio , conforme mostrado na figura.
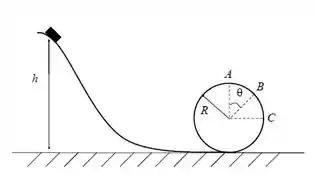
- Qual é o menor valor de (chame este valor ) necessário para que o carrinho faça a volta completa do loop?
- Se , o carrinho cai do trilho em um ponto B, quando ainda falta percorrer mais um ângulo para chegar até o topo A. Calcule .
- Suponha que agora, por alguma razão, haja atrito cinético entre o carrinho e o trilho. Sabendo que o carrinho foi solto (no repouso) da altura e que ele passou no ponto C do loop com velocidade escalar , qual é o trabalho realizado pela força de atrito até o ponto C?
Questão 14
[ENUNCIADO COMUM ÀS QUESTÕES 1, 2 e 3 do 2°EE 2017.2]
Um esquiador de massa parte do repouso do ponto A, a uma altura acima da extremidade de uma rampa para saltos de esqui. Ele deixa a rampa no ponto B, fazendo um ângulo com a horizontal. O esquiador então atinge sua altura máxima no ponto C. Despreze os efeitos da resistência do ar e do atrito com a rampa. Dados: ; e .
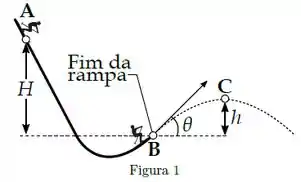
[Questão 1]
Considere as seguintes afirmações:
(I) A variação da energia potencial gravitacional do esquiador entre os pontos A e B é negativa.
(II) A variação da energia cinética do esquiador entre os pontos A e C é negativa.
(III) A variação da energia mecânica do esquiador entre os pontos B e C é positiva.
Das afirmações acima, são verdadeiras apenas:
(a) I
(b) II
(c) III
(d) I e II
(e) I e III
(f) II e III
(g) Todas
(h) Nenhuma
Ver solução completaQuestão 15
[ENUNCIADO COMUM ÀS QUESTÕES 1, 2 e 3 do 2°EE 2017.2]
Um esquiador de massa parte do repouso do ponto A, a uma altura acima da extremidade de uma rampa para saltos de esqui. Ele deixa a rampa no ponto B, fazendo um ângulo com a horizontal. O esquiador então atinge sua altura máxima no ponto C. Despreze os efeitos da resistência do ar e do atrito com a rampa. Dados: ; e .
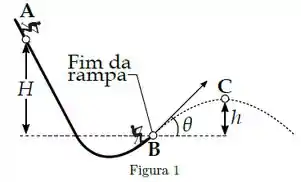
[Questão 2]
O módulo da velocidade do esquiador em B é:
(a)
(b)
(c)
(d)
(e)
(f)
(g)
(h)
Ver solução completaQuestão 16
Um carro em um parque de diversões de parte do repouso do ponto A e se desloca sem atrito trilho abaixo em direção a um loop como mostrado na figura a seguir.
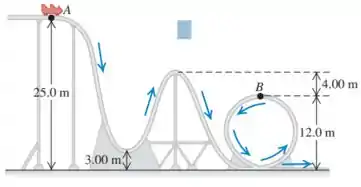
(a) Qual a velocidade escalar do carro no ponto B?
Ver solução completaQuestão 17
1) Uma criança de massa desliza em um escorregador irregularmente curvo de altura , como mostrado na figura ao lado. A criança começa do repouso no topo.
(a) Determine a velocidade escalar da criança na base, supondo que nenhum atrito esteja presente.

Questão 20
O pêndulo de Newton é um dispositivo formado por uma série de esferas suspensas em um único suporte por cordas de igual comprimento, que atuam como pêndulos idênticos adjacentes um ao outro, como ilustrado na figura abaixo. Podemos modificar esse dispositivo alterando a massa de uma das esferas (em preto) de para . Suponho os seguinte experimentos:
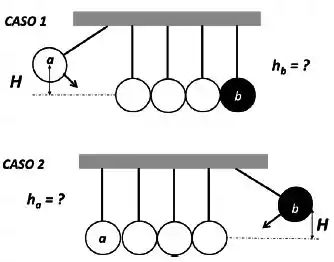
Caso 1: A esfera de massa é deslocada para esquerda e liberada, deslocando-se para direita e colidindo elasticamente com as demais esferas, inicialmente em repouso. Após a primeira colisão, a esfera de massa na extremidade oposta eleva-se de em relação ao plano dos pêndulos em repouso.
Caso 2: A esfera de massa é deslocada para direita e liberada, deslocando-se para esquerda e colidindo elasticamente com as demais esferas de massas , inicialmente em repouso. Após a primeira colisão, a esfera na extremidade oposta eleva-se de em relação ao plano dos pêndulos em repouso.
Considerando o triplo de . A razão entre as alturas de e nos casos é:
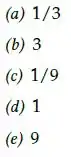
Questão 21
Um bloco encontra-se em equilíbrio suspenso por uma mola de constante elástica , presa ao teto e com alongamento . O bloco é levantado até a posição em que a alongação é nula e abandonado a partir do repouso. Ao descer uma altura o bloco ganha uma energia cinética igual a:
Questão 22
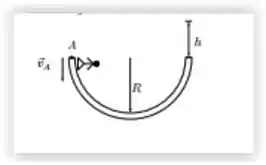
Um skatista brinca em uma pista em forma de semicircunferência de raio R, com atrito desprezível, como mostrado na figura. Se o atleta sai do ponto A com velocidade , a altura h máxima que ele atinge, em relação à borda da pista, é:
- 0
Questão 23
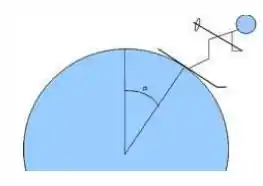
Um pequeno objeto, de massa começa a deslizar (com velocidade que pode ser considerada nula) do topo de um hemisfério de raio , que pode ser considerado perfeito. A partir daí, o objeto, que pode ser considerado uma partícula, se move seguindo o hemisfério, conforme a figura
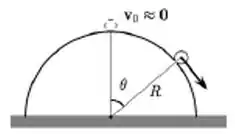
Considerando que o objeto está sempre em contato com o hemisfério, e que o atrito pode ser desprezado, qual o módulo da força que o objeto exerce sobre o hemisfério quando ele se encontra na posição indicada na figura, cujo raio faz um ângulo com a vertical?
a)
b)
c)
d) A força é nula
e)
Ver solução completaQuestão 25
No sistema mostrado na figura abaixo, dois blocos de massas M=3,00kg e m=1,00kg estão conectados por um cabo inextensível de massa desprezível que passa por uma polia fixa ao teto. O bloco de massa M é solto a partir do repouso desde uma altura inicial h=2,00m, fazendo a polia de massa desprezível girar sem atrito até que o bloco toque o solo. A energia cinética do bloco de massa M imediatamente antes de tocar o solo é:
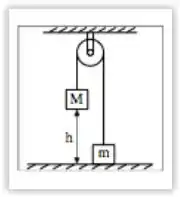
(A) =39,2 J
(B) =58,8 J
(C) =29,4 J
(D) =19,6 J
(E) = 9,80 J
Ver solução completaQuestão 26
Considere o sistema de blocos de massas M=3 kg e m=1 kg que estão conectados por um cabo inextensível de massa desprezível que passa por uma polia fixa ao teto. O bloco de massa M é solto a partir do repouso desde uma altura h=2 m fazendo a polia de massa desprezível girar sem atrito até que o bloco toque o solo.
Seja a energia potencial gravitacional no instante inicial em que o bloco de massa M é solto, e Kf a energia cinética final do sistema no instante em que o bloco de massa M toca o solo. A fração de convertida em energia cinética desde o instante inicial até o instante final é:
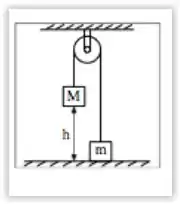
(A) 1
(B) 2/3
(C) 1/2
(D) 1/6
(E) 1/3
Ver solução completaQuestão 27
Uma granada explode em três fragmentos iguais de massa . Após a explosão, o primeiro fragmento vai para o oeste e os outros dois nas seguintes direções: ao norte e ao sul, ambos em relação à direção leste. A energia cinética total liberada foi de . Quais são os módulos das velocidades iniciais dos 3 fragmentos, logo após a explosão?
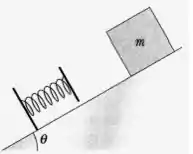
Ver solução completaQuestão 28
Um bloco começa deslizar a partir do repouso no topo de um plano inclinado de 30,0° e encontra uma mola de constante 3,40kN/m, fixada rigidamente ao plano. Se a massa do bloco é de 34,0 kg e comprime a mola de 37,0 cm até parar, encontre a distância percorrida pelo bloco antes de encontrar a mola. (Considere g = 10,0 m/s2).
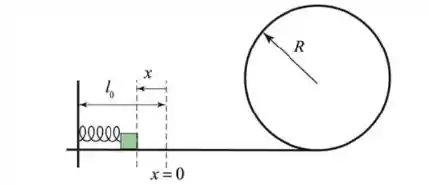
a) 1,00m
b) 1,37m
c) 0,740m
d) 0,820m
e) 0,440m
Ver solução completaQuestão 29
(Cap 7 – Ex 39) O objeto de da Figura 7-42 é liberado do repouso a uma altura de em uma rampa curva sem atrito. Na base da rampa está uma mola com uma constante de força igual a . O objeto desliza rampa abaixo até a mola, comprimindo-a uma distância até atingir momentaneamente o repouso.
(a) Encontre .
(b) Descreva o movimento do objeto (se ocorrer) após o repouso momentâneo ?

Questão 30
Seja o salto de bungee jump mostrado ao lado nas seguintes três etapas: Posição – o saltador de massa se encontra em sua posição inicial com velocidade inicial igual a zero. Posição – o saltador caiu uma altura exatamente igual ao comprimento da corda relaxada. Após cair esta altura seu movimento passa também a estar sob ação da força elástica da corda. Posição – o saltador encontra sua posição de retorno com distensão máxima 𝑑 da corda e velocidade igual a zero. Sabendo que o comprimento da corda relaxada é e supondo sua constante elástica , despreze a resistência do ar e determine:
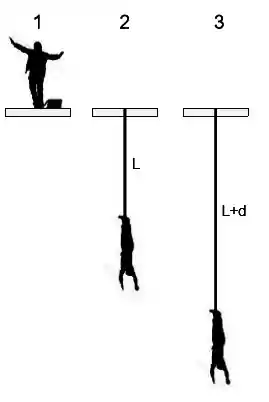
(a) A velocidade do saltador na posição .
(b) Sua velocidade máxima.
(c) A altura mínima da posição inicial para que o salto seja seguro.
Ver solução completaQuestão 31
Uma partícula de massa está sujeita a um potencial , onde é dado em metros e em Joules, representado graficamente na figura.
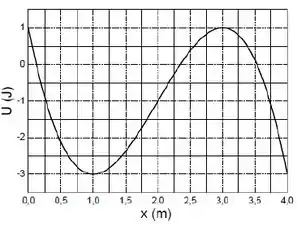
- Determine a força F(x) atuando na partícula e represente-a graficamente.
- Identifique os pontos de equilíbrio e classifique-os (estável ou instável).
- Em , a partícula é abandonada a partir do repouso. Em que direção e sentido a partícula passará a se mover? Qual é o módulo da força que atua nela neste ponto?
- Para a condição inicial do item (c), em que ponto a velocidade da partícula será máxima e qual será o seu valor?
- Para a condição inicial do item (c), quais serão, aproximadamente, os valores máximo e mínimo de para essa partícula?
Questão 32
. Uma partícula se aproxima de uma rampa em forma de meio semicírculo, conforme figura,
com uma velocidade tal que a partícula atinge o topo da rampa, e retorna pelo mesmo trajeto.
Desconsiderando qualquer força de atrito, qual das afirmações abaixo é verdade sobre a
partícula no ponto P?
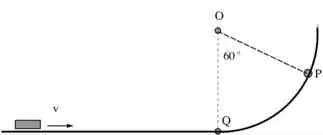
A sua energia cinética é zero.
A energia potencial gravitacional adquirida desde o início da rampa tem módulo igual ao
módulo da energia cinética.
A força peso não realiza torque em relação a um eixo que passa pelo ponto O.
A força normal é a única responsável pelo movimento circular, atuando como a força centrípeta no movimento de subida na rampa circular.
A energia cinética no ponto P e ponto Q são iguais porque não há atrito.
Ver solução completaQuestão 33
Uma bola cai uma certa distância e perde de energia potencial gravitacional. Não despreze a resistência do ar. Quanta energia cinética a bola ganha?
(a) mais do que .
(b) exatamente .
(c) menos do que .
(d) exatamente .
(e) exatamente .
Ver solução completaQuestão 34
4) Considere o gráfico a seguir, onde a linha curva representa a energia potencial de uma partícula, que se movimenta em uma dimensão, e a linha reta, horizontal, a sua energia mecânica (ambas em Joules) em função da sua posição (em m).
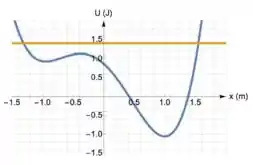
Sejam as afirmativas abaixo:
- O movimento da partícula possui dois pontos de retorno.
- A partícula tem velocidade máxima em
- A força que atua na partícula se anula nos pontos de interseção entre curvas de energia potencial e energia mecânica.
São VERDADEIRAS apenas:
(a) Todas
(b) e
(c)
(d)
(e)
Ver solução completaQuestão 35
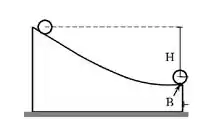
9) Uma casca esférica homogênea de massa M e raio R é solta do repouso de modo a descer por uma rampa, vindo a abandoná-la a partir de sua extremidade em B, após descer uma altura H, conforme ilustrado na figura. Desconsiderando a resistência do ar e assumindo que a casca nunca perca o contato com a superfície da rampa, a velocidade do centro de massa da casca esférica ao chegar ao ponto B será:
Questão 36
Considere o movimento de uma partícula de energia mecânica total , sob a ação de forças conservativas. Dentre as alternativas ao lado identifique aquela que representa corretamente como a energia cinética de tal partícula varia em função de sua energia potencial :
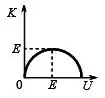 (a)
(a)
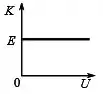 (b)
(b)
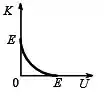 (c)
(c)
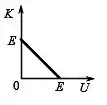 (d)
(d)
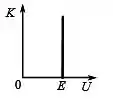 (e)
(e)
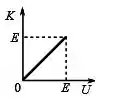 (f)
(f)
Questão 37
A figura mostra o perfil de um trilho contido no plano vertical, sendo o trecho circular, de centro e de raio . Umas esfera de pequenas dimensões é abandonada a uma altura acima do plano horizontal que contém o centro , passando a deslizar sobre o trilho com atrito desprezível. O módulo da força que o trilho exerce sobre a esfera no instante em que ele passa pelo ponto é
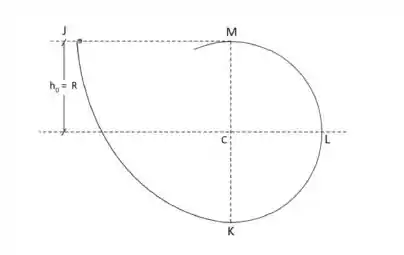
a)
b)
c)
d)
e)
f) nulo
Ver solução completaQuestão 38
Um bloco de massa encontra-se em repouso sobre uma superfície horizontal sem atrito, preso a um suporte rígido, por uma mola de constante , conforme ilustrado abaixo. Uma bala de massa e velocidade atinge o bloco e permanece dentro do bloco.
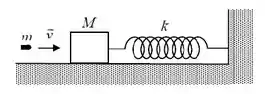
Determine, em termos de , a amplitude do movimento harmônico simples resultante é:
Questão 39
Um bate-estaca de gravidade funciona com um princípio muito simples. Um martelo de massa é solto do repouso a uma altura acima de uma estaca de massa . A colisão dura um intervalo de tempo muito curto . Imediatamente após a colisão o martelo e a estaca adquirem a mesma velocidade e chegam ao repouso, depois de afundarem uma distância . Suponha o intervalo de tempo de afundamento como sendo . Todo movimento acontece ao longo da direção vertical. Utilize o sistema de coordenadas abaixo, dê suas respostas em função dos dados do problema e dos vetores unitários e . Utilize para o módulo da aceleração da gravidade.
(a) Determine qual é a velocidade com que o martelo chega na estaca.
Ver solução completaQuestão 40
A figura mostra um trilho perfeitamente liso contido em um plano vertical. Uma partícula é abandonada em repouso no ponto do trilho e desliza sobre ele sem nunca perder contato. A partícula passa pelos pontos , e e atinge o ponto , localizado na mesma altura que .
No percurso de a , a energia cinética é:
(a) Máxima em
(b) Mínima e igual em e
(c) Nula apenas em e
(d) Nula em , , , e
(e) Nula apenas em
Ver solução completaQuestão 41
Um bloco de escorrega para baixo, a partir do repouso, em um plano inclinado que faz um ângulo de com a horizontal. O coeficiente de atrito cinético é de .
No instante em que o bloco percorre dois metros, qual a variação da energia térmica do sistema Terra-bloco?
Ver solução completaQuestão 42
Um corpo de massa move-se ao longo do eixo preso a uma mola de constante elástica . A mola fica relaxada quando o corpo está na posição . A velocidade do corpo em é de no sentido positivo do eixo . Qual é sua velocidade quando ele passa por ?
(a)
(b)
(c)
(d)
(e)
(f)
(g)
(h)
(i)
Ver solução completaQuestão 43
Um bloco de massa é solto a partir do repouso de uma altura e escorrega ao longo de um aro circular sem atrito de raio , como mostrado na figura abaixo. O módulo da aceleração da gravidade é . Qual das seguintes expressões dá a velocidade da massa na parte inferior do aro?
a)
b) zero.
c)
d)
e)
Ver solução completaQuestão 44
Um bloco de massa encontra-se a uma altura a partir do topo de uma mola relaxada de constante elástica . Use para a aceleração da gravidade. Após o bloco ser solto e tocar a mola, determine em termos de , e :
a) Qual a compressão da mola onde o bloco tem aceleração nula?
b) Determine a máxima compressão da mola.
Ver solução completaQuestão 45
A energia potencial de uma partícula que se move ao longo do eixo é dada por , onde está em joules e em metros. Se a energia mecânica total é , os limites de seu movimento são:
a) e
b) e 2
c) e
d) e
e) e
Ver solução completaQuestão 46
A figura mostra três partículas lançadas do mesmo nível com velocidades iniciais de mesmo módulo. A primeira é lançada verticalmente, a segunda fazendo um ângulo () com a horizontal e a terceira é lançada sobre um plano inclinado liso com ângulo de inclinação também igual a , como indica a figura. As três partículas passam por uma altura com rapidezes respectivas. Despreze a resistência do ar. Podemos afirmar que:
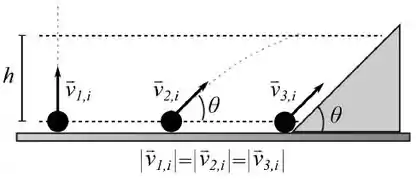
(A)
(B)
(C)
(D)
(E)
Ver solução completaQuestão 47
Seja um plano inclinado de um ângulo com a horizontal, com coeficientes de atrito cinético e estático iguais a e , respectivamente. No seu topo, um objeto de massa é mantido em repouso através de um freio. Ele está conectado a um cabo que passa por uma roldana e que está preso a uma mola na vertical de constante elástica desconhecida. A outra extremidade da mola está presa ao solo. Nesta situação a mola está relaxada. Quando o freio é retirado, o objeto desliza plano abaixo uma distância até ser parado pela força da mola esticada.
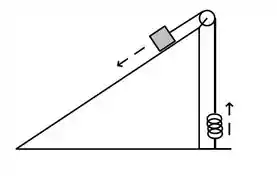
Considerem o cabo, a roldana e a mola sem massa e ideais. Responda em função dos dados do problema.
a) Determine a variação da energia cinética do objeto do início ao final do trajeto.
b) Determine a variação da energia potencial gravitacional do objeto do início ao final do trajeto.
c) Determine o trabalho realizado pelo atrito do início ao final do trajeto.
d) Escreva para esta situação específica a equação de conservação de energia apropriada.
e) Determine a energia potencial elástica armazenada na mola ao final do trajeto.
Ver solução completaQuestão 48
São lançadas verticalmente para cima duas bolas idênticas, a bola com velocidade e a bola com velocidade . Desprezando a resistência do ar, qual das afirmativas sobre estas bolas é correta?
A bola alcançará duas vezes a altura da bola porque tinha duas vezes a velocidade inicial.
A bola alcançará quatro vezes a altura da bola porque tinha quatro vezes a energia cinética inicial.
As bolas alcançarão a mesma altura porque elas têm a mesma massa e a mesma aceleração.
Na sua altura máxima, a bola terá duas vezes a energia potencial gravitacional da bola porque partiu duas vezes mais rápida.
Nas alturas máximas, a aceleração de cada bola é instantaneamente igual a zero porque elas param por um instante.
Ver solução completaQuestão 49
Pedrinho foi ao mercado com sua mãe e, apesar de todos os avisos, ele aproxima-se da prateleira de refrigerantes em lata que fica a uma altura de e acaba derrubando uma das latas da prateleira
Considerando que a energia potencial da lata na prateleira é , com qual velocidade ela atinge o solo?
(considere )
a)
b)
c)
d)
e)
Ver solução completaQuestão 50
Um passeio de montanha-russa num parque de diversões parte do repouso a uma altura de acima do solo e rapidamente inicia a descida pelo trilho. Num certo momento, a pista faz um loop e o trem atinge uma uma altura de . Qual a velocidade do trem nesse momento, considerando que a carga completa do trem mais as pessoas sobre ele tem uma massa de ? (considere )
(a) s
(b)
(c)
(d)
(e)
Ver solução completaQuestão 51
Uma partícula de massa m = 2,0 kg move-se ao longo do eixo x sujeita a uma única força F. A dependência de F com a posição x da partícula é mostrada na Figura 1. A energia potencial associada à forçaa F é U. Quando a partícula está em x = 0, ela tem velocidade = 2,0 m/s no sentido positivo do eixo x.
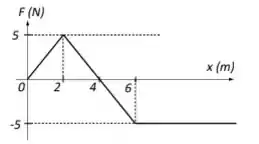
A energia cinética da partícula na posição x = 4,0 m é:
a) 0 J
b) 4 J
c) 10 J
d) 14 J
e) 24 J
f) 25 J
g) 49 J
h) 100 J
i) 144 J
Ver solução completaQuestão 52
Dois blocos, de massas M = 3,0 kg e m = 1,0 kg, são inicialmente mantidos em repouso sobre uma superfície horizontal, comprimindo uma mola ideal. Ao serem simultaneamente liberados da mola, cada bloco viaja para um lado e sobe uma rampa inclinada. Considere que a velocidade do bloco de massa M logo após ser liberado é V = 3,0 m/s. Despreze todos os atritos e use
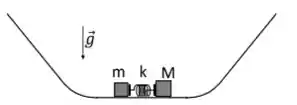
Qual é a variação da energia potencial elástica (em módulo) antes e depois dos blocos serem liberados?
a) 10 J
b) 12 J
c) 24 J
d) 28 J
e) 36 J
f) 42 J
g) 54 J
h) 58 J
Ver solução completaQuestão 53
Dois blocos, de massas M = 3,0 kg e m = 1,0 kg, são inicialmente mantidos em repouso sobre uma superfície horizontal, comprimindo uma mola ideal. Ao serem simultaneamente liberados da mola, cada bloco viaja para um lado e sobe uma rampa inclinada. Considere que a velocidade do bloco de massa M logo após ser liberado é V = 3,0 m/s. Despreze todos os atritos e use
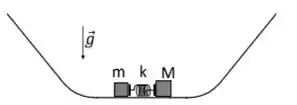
Qual é a altura máxima vertical (em metros), em relação â superfície horizontal, alcançada pelo bloco de massa M ao subir a rampa?
a) 0,20
b) 0,25
c) 0,30
d) 0,35
e) 0,40
f) 0,45
g) 0,50
h) 0,55
Ver solução completaQuestão 54
Um bloco de inicialmente em repouso cai sobre uma mola vertical inicialmente relaxada. A constante elástica desta mola vale . O bloco toca a mola e permanece em contato comprimindo-a em até parar momentaneamente. Adote . Nessa compressão, calcule:
(a) o trabalho realizado sobre a bloco pela força elástica (0,5)
(b) a compressão da mola quando a aceleração do bloco é nula (1,0)
(c) a velocidade do bloco imediatamente antes de se chocar com a mola (1,0)
(d) a altura de onde o bloco foi solto em relação ao topo da mola relaxada?
Ver solução completaQuestão 55
1) Uma criança de massa desliza em um escorregador irregularmente curvo de altura , como mostrado na figura ao lado. A criança começa do repouso no topo.
(b) Se uma força de atrito agir sobre a criança de e ela chega na base do ecorregador com velocidade escalar de , qual a redução da energia mecânica do sistema devido a presença desta força?

Questão 58
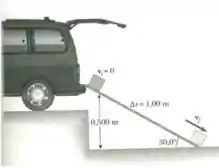
2) Uma caixa de desliza rampa abaixo em um galpão de carga. A rampa tem de comprimento e está inclinada a um ângulo de , como mostrado na figura abaixo. A caixa começa do repouso no topo e sofre a ação de uma força de atrito constante de módulo . Calcule a velocidade escalar da caixa quando ela atinge a parte mais inferior da rampa, pelos métodos de conservação de energia.
Questão 60
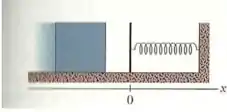
5) Considere a figura ao lado. O bloco de massa tem uma velocidade inicial e comprime a mola de constante elástica por uma distância até parar. (a) calcule desconsiderando o atrito.
Questão 61
Uma partícula em movimento unidimensional está sujeita à energia potencial mostrada no gráfico a seguir. Sua energia mecânica total está representada pela linha tracejada. A posição inicial da partícula é com velocidade negativa.
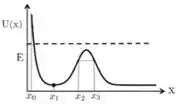
Considere as afirmativas a seguir:
– É impossível que a partícula atinja a posição
– A velocidade da partícula no pico da curva (entre e ) é nula;
– As forças sobre a partícula nas posições e são iguais.
Escolha uma:
Somente é verdadeira.
Somente é verdadeira.
Somente é verdadeira.
e são verdadeiras.
e são verdadeiras.
e são verdadeiras.
Todas são verdadeiras.
Todas são falsas.
Ver solução completaQuestão 62
Qual das afirmativas abaixo é a CORRETA?
- O valor da energia mecânica associada a uma partícula nunca pode ser negativo.
- É possível associar uma energia potencial a qualquer força que atue sobre um corpo.
- O valor da energia potencial associada a uma partícula nunca pode ser negativo.
- Para a energia cinética de uma partícula se conservar, é necessário que o trabalho total realizado pelas forças dissipativas sobre a mesma seja nulo.
- O trabalho total realizado pelas forças que atuam sobre uma partícula é sempre igual à variação da energia cinética da mesma.
Questão 63
Dois blocos de massas e estão conectados por um cabo de massa muito pequena que passa por uma polia de massa também irrisória, que gira sem atrito, conforme mostra a figura ao lado. Considerando-se que na posição inicial a mola, de constante elástica , não exerce força sobre o bloco , calcule:
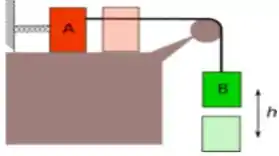
a) A máxima elongação (h) da mola quando o bloco desliza sem atrito.
b) A máxima elongação (h) da mola na presença de atrito, com coeficiente de atrito cinético .
Ver solução completaQuestão 64
A figura abaixo mostra como a força exercida pelo fio de um arco varia em função da distância em que a flecha é puxada para trás (o comprimento de deformação). Suponha que a mesma força seja fornecida para a flecha que se move para frente quando o fio é liberado. A deformação máxima para esse arco corresponde a um comprimento de deformação igual a . Se o arco atira uma flecha de quando ele está submetido a uma deformação máxima, qual é a velocidade da flecha quando ela abandona o arco?
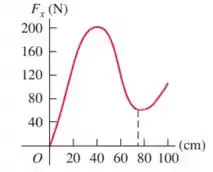
Questão 65
Um pequeno bloco de massa desliza em um círculo vertical de raio por uma faixa circular. Não existe atrito entre a faixa e o bloco. Enquanto o bloco se encontra no ponto mais baixo de seu caminho, a força normal que a faixa exerce no bloco tem módulo de . Encontre o módulo da força normal que a faixa exerce no bloco quando este está localizado no ponto mais alto do caminho.
Ver solução completaQuestão 66
Em uma superfície horizontal sem atrito, um bloco colide com uma mola colada a outro bloco, o qual está inicialmente em repouso. Quando a compressão da mola é máxima, ambos os blocos possuem a mesma velocidade. Considerando o instante imediatamente anterior à colisão e o instante de compressão máxima da mola, quais quantidades são conservadas?
(A) momento linear e energia mecânica
(B) apenas o momento linear
(C) apenas a energia cinética
(D) momento linear e energia cinética
(E) momento linear e energia potencial
Ver solução completaQuestão 67
Um bloco inicialmente em repouso é solto do alto de uma rampa inclinada sem atrito. Quando ele chega à base da rampa, sua velocidade é . De quantas vezes devemos aumentar a altura da rampa para que o bloco chegue na base com o dobro desta velocidade?
a) 1 vez.
b) 2 vezes.
c) 3 vezes.
d) 4 vezes.
e) nenhuma das respostas acima
Ver solução completaQuestão 68
Um bloco de massa é liberado, com velocidade inicial , a uma altura . Desprezando a resistência do ar, o bloco desliza sobre um trilho sem atrito de acordo com a figura abaixo:
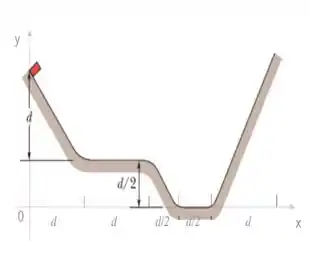
a) Calcule a velocidade do bloco ao chegar no segundo trecho plano do trilho.
(b) Determine a altura atingida pelo bloco no último trecho do trilho.
(c) Esboce, numa única figura, a energia cinética, a energia potencial gravitacional e a energia total do bloco durante percurso entre e 3d. Identifique no gráfico a posição do bloco em cada trecho.
(d) Considere que a superfície do primeiro trecho plano do trilho dissipe de energia do bloco devido ao atrito. Recalcule a altura que o bloco atingirá o último trecho do trilho nessa situação
Ver solução completaQuestão 69
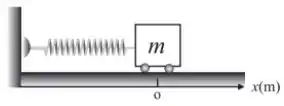
. Uma mola tem uma extremidade fixa em uma parede vertical e a outra num carrinho de massa , que movimenta-se como uma partícula numa superfície horizontal sem atrito, sujeita a uma força elástica dada por . Se o carrinho passa pela posição com velocidade , sua velocidade escalar ao passar pela posição , em metros por segundo, é:
Questão 71
Um bloco é lançado do ponto em uma pista horizontal com velocidade inicial . A pista apresenta um vale de profundidade e em seguida uma rampa que atinge uma altura com relação à altura do ponto , conforme a figura. Não há atrito entre o bloco e a rampa exceto na parte superior horizontal da pista, a partir do ponto . Deste ponto em diante, o bloco percorre uma distância D até parar. Em todo o percurso, o bloco mantém contato com a pista. Considere as seguintes afirmações:
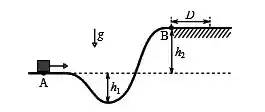
I) Se diminuímos (mantendo ), o bloco percorre uma distância maior que .
II) Se diminuímos (mantendo ), o bloco percorre uma distância maior que .
III) Se dobramos sua massa, o bloco percorre o dobro da distância .
Quais afirmações são verdadeiras?
(a) Apenas I
(b) Apenas III
(c) I e III
(d) Todas
(e) Apenas II
(f) I e II
(g) II e III
(h) Nenhuma
Ver solução completaQuestão 72
Um pequeno bloco parte do repouso no ponto e desliza sobre uma calha. Sabe-se que há atrito entre o bloco e a calha. Ao abandonar a calha, o bloco percorrerá a trajetória que está representada por uma linha tracejada. Qual a figura que representa corretamente a trajetória?
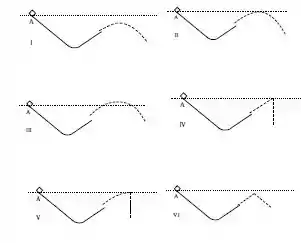
a) I
b) II
c) III
d) IV
e) V
f) VI
Ver solução completaQuestão 74
Uma bola rola a partir do repouso em diferentes rampas com atrito praticamente nulo. Em qual das rampas a bola chega com maior rapidez no final?
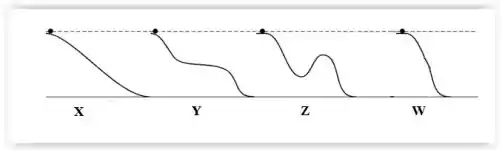
A) A rampa X.
B) A rampa Y.
C) A rampa Z.
D) A rapidez final será a mesma em todas as rampas.
E) A rampa W.
Ver solução completaQuestão 75
Um projétil é lançado do solo numa direção que faz um ângulo com a horizontal. Desprezando-se a resistência do ar e tomando o zero da energia potencial no nível de lançamento, a razão entre a energia cinética e a energia mecânica do projétil quando ele atingir a altura máxima é
(a)
(b)
(c)
(d)
(e)
Ver solução completaQuestão 76
. Um fruto cai de uma árvore. Então:
ambas as energias cinética e potencial gravitacional permanecem constantes;
sua energia cinética diminui e sua energia potencial gravitacional aumenta;
sua energia cinética aumenta e sua energia potencial gravitacional diminui;
sua energia cinética aumenta e sua energia potencial gravitacional aumenta;
sua energia cinética diminui e sua energia potencial gravitacional diminui;
Ver solução completaQuestão 77
Uma partícula de massa m = 0,5 kg move-se em um campo de força central sob a ação
de uma força F(r) em uma região onde a energia potencial U(r) varia conforme a figura abaixo. Supondo que a partícula tenha energia total E = -3 J, a máxima velocidade da partícula e o trabalho realizado pela força F(r) para deslocar a partícula desde r = 1m até r = 4 m são, respectivamente:
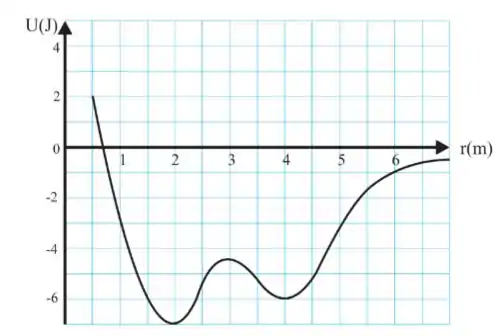
a) v=2m/s e W=8J
b) v=m/s e W=-3J
c) v=4m/s e W=3J
d) v=m/s e W=-6
e) v=4m/s e W=-3J
Ver solução completaQuestão 78
Um coco maduro desprende-se de um coqueiro a uma distância de do solo. Determine a velocidade do coco no instante imediatamente anterior a ele tocar o solo. (considere )
(a)
(b)
(c)
(d)
(e)
Ver solução completaQuestão 79
Um bloco de massa encontra-se em um plano inclinado de um ângulo , com e . Uma mola de constante elástica tem uma extremidade presa à parte superior do plano e a outra presa ao bloco. Inicialmente o bloco está parado e a mola está relaxada. Não há atrito no problema e . O bloco desce ao ser liberado. Quando o bloco está a uma distância da posição inicial (medida ao longo do plano inclinado), qual é a sua energia cinética?
Questão 80
(Capítulo 8.5 – Exercício 23) Em , uma bola de é atirada de uma torre com . Quanto é do sistema bola-Terra entre e (ainda em queda livre)?
Ver solução completaQuestão 81
(Cap 6 – Ex 2) Você empurra uma caixa pesada sobre uma mesa horizontal com atrito, em linha reta. A caixa parte do repouso e acaba em repouso. Descreva o trabalho realizado sobre ela (incluindo sinais) por cada uma das forças que atuam sobre ela e diga qual é o trabalho resultante realizado.
Ver solução completaQuestão 82
(Cap 7 – Ex 38) Um bloco de desliza ao longo de uma superfície horizontal sem atrito com uma velocidade de (Figura 7-41). Após deslizar por uma distância de , o bloco faz uma suave transição para uma rampa sem atrito inclinada a um ângulo de 40° com a horizontal. Qual a distância, ao longo da rampa, que o bloco percorre até atingir momentaneamente o repouso?

Questão 83
(Cap 7 – Ex 51a) Uma bola (de ) é lançada do teto de um edifício, acima do chão. Sua velocidade inicial é de , formando acima da horizontal. Despreze a resistência do ar.
a) Qual a altura máxima, acima do chão, atingida pela bola?
Ver solução completaQuestão 84
A figura mostra a função energia potencial U(x) de uma partícula. Qual é o maior valor possível da energia mecânica Emec para o qual a partícula não consegue ir além do ponto H?
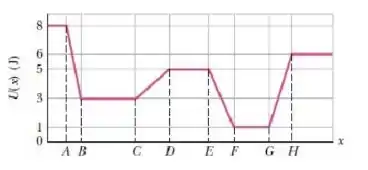
a) 7 J
b) 6 J
c) 5 J
d) 3 J
e) 1 J
Ver solução completaQuestão 86
(Cap 7 – Ex 51b) Uma bola (de ) é lançada do teto de um edifício, acima do chão. Sua velocidade inicial é de , formando acima da horizontal. Despreze a resistência do ar.
b) Qual é a rapidez da bola ao chegar no chão
Ver solução completaQuestão 87
Um atleta, durante uma das fases de uma competição, teve que descer uma rampa com forte vento contrário ao seu movimento; com muito esforço, o atleta conseguiu manter sua velocidade constante. Podemos afirmar que:
(a) a energia potencial gravitacional está diminuindo;
(b) a energia mecânica foi conservada;
(c) sua energia cinética está aumentando;
(d) a energia potencial gravitacional está aumentando;
(e) as energias cinética e potencial estão aumentando;
Ver solução completaQuestão 88
Os carrinhos de brinquedo podem ser de vários tipos. Dentre eles, há os movidos a corda, em que uma mola em seu interior é comprimida quando a criança puxa o carrinho para trás. Ao ser solto, o carrinho entra em movimento enquanto a mola volta à sua forma inicial. O processo de conversão de energia que ocorre no carrinho descrito também é verificado em:
- Uma atiradeira (estilingue)
- Um motor a combustão
- Uma usina hidroelétrica
- Um freio de automóvel
- Um dínamo
Questão 89
Imagine que você deixa cair (abandonando) um objeto de massa de uma altura de metros. Determine a velocidade desse objeto ao tocar o solo. Despreze a resistência do ar e considere .
(a)
(b)
(c)
(d)
(e)
Ver solução completaQuestão 90
(Cap 9 – Ex 73) No sistema do problema 71, se a prateleira (sem atrito) for ajustada com uma inclinação, qual deve ser essa inclinação para que os blocos se movam com uma rapidez constante?
Ver solução completaQuestão 91
Um bloco de massa desce uma rampa partindo do repouso de altura tomando como referência a parte inferior da rampa. Após iniciar a descida, o bloco passa por um ponto localizado na rampa em uma altura com velocidade e por um ponto localizado na rampa em uma altura com velocidade . Ao chegar à parte inferior, o bloco encontra uma plataforma horizontal e continua se deslocando até tocar e comprimir de uma mola de constante elástica fixa na horizontal.
- Determine o trabalho realizado pela força gravitacional sobre o bloco para ir do ponto até o ponto em função de , e .
- Determine a altura em função de e .
- Determine a velocidade na parte em um ponto na plataforma antes de tocar na mola em função de e .
- Determine a compressão máxima da mola em termos , , e .
- Se a massa inicial fosse dobrada, valendo , a velocidade no ponto aumentaria, diminuiria ou continuaria o mesmo em relação a situação com a massa ?
Questão 92
(Capítulo 8.5 – Exercício 16)
(a) No Problema 7, qual é a velocidade da bola no ponto mais baixo? (b) Essa velocidade aumenta, diminui ou permanece a mesma se a massa aumenta?
Ver solução completaQuestão 93
(Capítulo 8.5 – Exercício 24) Um esquiador de parte do repouso a uma altura acima da extremidade de uma rampa para saltos de esqui (Fig. 8-35) e deixa a rampa fazendo um ângulo com a horizontal. Despreze os efeitos da resistência do ar e suponha que a rampa não tenha atrito. (a) Qual é a altura máxima do salto em relação à extremidade da rampa? (b) Se o esquiador aumentasse o próprio peso colocando uma mochila nas costas, seria maior, menor ou igual?

Questão 94
Na Fig. 8-40, um bloco de massa desliza para baixo, a partir do repouso, percorre uma distância em um plano inclinado de ângulo e se choca com uma mola de constante elástica . Quando o bloco para momentaneamente, a mola fica comprimida . Quais são (a) a distância e (b) a distância entre o ponto do primeiro contato do bloco com a mola e o ponto onde a velocidade do bloco é máxima?
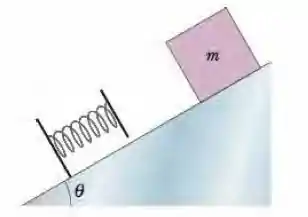
Figura 8-40 Problema 35
Ver solução completaQuestão 95
3) Considere uma partícula de massa que é solta do repouso do alto de uma altura de três maneiras distintas. Em nenhum dos casos, há atrito entre o plano e a partícula.
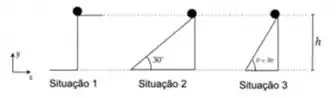
Sejam e os módulos das componentes das velocidades na direção e , e , o trabalho realizado pela força peso após a partícula descer de uma altura nas três situações, é correto afirmar que:
(a) e
(b) e
(c) e
(d) e
(e) e
Ver solução completaQuestão 96
9) Um bloco de massa que se encontra encostado à extremidade livre de uma mola de constante elástica é impulsionado em direção a uma rampa inclinada de um ângulo após percorrer um trecho horizontal.
- Na situação , a mola está comprimida em e não existe atrito em nenhum dos dois trechos do percurso.
- Na situação , a mola está comprimida em e existe atrito apenas no trcho inclinado, cujos coeficientes estático e cinético são, respectivamente, e .
Sempre que necessário, considere a aceleração da gravidade no local.
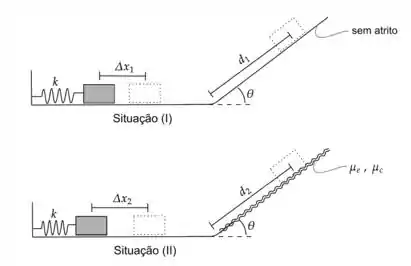
- Na situação qual a velocidade do bloco imediatamente após se desprender da mola?
- Na situação , calcule a distância percorrida pelo bloco na rampa até atingir o repouso. Expresse sua resposta em termos de e .
- Na situação , represente o diagrama de forças que atuam no bloco quando ele está subindo na rampa inclinada.
- Na situação encontre , onde é a distância percorrida pelo bloco na rampa até atingir o repouso. Calcule qual deve ser o valor da compressão para que
Questão 97
Considere um sistema composto pelo planeta Terra e por uma bola de massa m=0,200 kg. A bola é abandonada do repouso de uma altura H=5 m, e retorna, após quicar no chão, a uma altura h=H/4. Calcule:
a) a velocidade da bola logo antes e logo depois do contato com o chão;
b) impulso exercido na bola pelo chão e o impulso exercido no chão pela bola;
c) trabalho exercido pelas forças dissipativas em ação;
d) a colisão da bola com o chão conserva momento linear? Justifique.
e) Suponha agora que o trabalho exercido pelas forças dissipativas em ação seja reduzido para 2/3 do valor. Após quicar no chão, que altura a bola alcançará agora?
Ver solução completaQuestão 99
Questão 7
Considera quatro objetos, A.B,C e D. Observou-se que A e B estão em equilíbrio térmico entre si. O mesmo para C e D. Entretanto, A e C não estão em equilíbrio térmico entre si. Pode-se concluir que:
(a) B e D estão à mesma temperatura.
(b) B e D podem estar em equilíbrio térmico, mas também podem não estar.
(c) B e D não podem estar à mesma temperatura.
(d) a Lei Zero da Termodinâmica não se aplica a este caso, porque existem mais de três objetos.
(e) A, B, C e D estão à mesma temperatura.
Ver solução completaQuestão 100
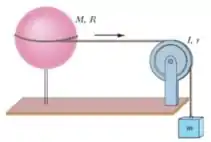
21) Uma casca esférica uniforme de massa e raio pode girar em torno de um eixo vertical sem atrito. Uma corda de massa desprezível está enrolada no equador da casca, passa por uma polia com momento de inércia e raio e está presa a um bloco de massa . Não há atrito no eixo da polia e a corda não escorrega na casca nem na polia. Qual é a velocidade do bloco depois de cair após ter sido liberado do repouso?
Questão 101
Uma bola de massa m = 0, 5 kg é presa a um pino por um o leve e inextensível de 0, 8 m de comprimento. A bola é abandonada quando está na horizontal. Na parte mais baixa da trajetória a bola atinge um bloco de massa M = 2, 0 kg, inicialmente em repouso sobre uma superfície áspera. A colisão, entre a bola e o bloco, pode ser considerada como perfeitamente elástica. O coeficiente de atrito cinético entre o bloco e a superfície é µc = 0, 16.
c. Até que altura sobe a bola após a colisão?
Ver solução completaQuestão 102
Uma bola de massa m = 0, 5 kg é presa a um pino por um o leve e inextensível de 0, 8 m de comprimento. A bola é abandonada quando está na horizontal. Na parte mais baixa da trajetória a bola atinge um bloco de massa M = 2, 0 kg, inicialmente em repouso sobre uma superfície áspera. A colisão, entre a bola e o bloco, pode ser considerada como perfeitamente elástica. O coeficiente de atrito cinético entre o bloco e a superfície é µc = 0, 16.
d. Qual a distância percorrida pelo bloco depois da colisão?
Ver solução completaQuestão 103
Num choque entre dois corpos de massas e , o primeiro desvia 90◦ de sua trajetória original, mantendo inalterada sua energia cinética. Se as velocidades iniciais dos corpos eram, respectivamente, e :
b. Verifique se o choque foi elástico ou inelástico.
Ver solução completaQuestão 104
Uma bala de massa igual a 4, 5 g é disparada horizontalmente num bloco de madeira de massa igual a 2, 4 kg, em repouso sobre a superfície horizontal. O coeficiente de atrito cinético entre o bloco e a superfície vale 0,20. A bala fica retida no bloco que sofre um deslocamento de 1, 8 m até o repouso.
a. Qual a velocidade do bloco imediatamente após a bala parar em seu interior?
Ver solução completaQuestão 105
Um satélite meteorológico de precisa ser colocado em uma órbita circular acima da superfície terrestre. Determine: a) a velocidade, o período e a aceleração centrípeta desse satélite? b) calcule a diferença entre a energia mecânica total, quando o satélite está em órbita, e a energia mecânica total, quando o satélite estava em repouso na plataforma de lançamento na Terra. Observação: essa diferença é igual ao trabalho necessário para colocar esse satélite em órbita.
Ver solução completaQuestão 106
35. Um alçapão quadrado de lado e massa está levantado verticalmente, em equilíbrio sobre as dobradiças, quando é levado a cair por uma ligeira trepidação. Desprezando o atrito, que velocidade angular terá adquirido ao bater no chão?
Ver solução completaQuestão 107
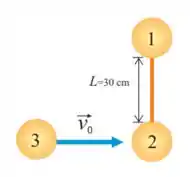
33. Um haltere formado por dois discos e iguais de massa unidos por uma barra rígida de massa desprezível e comprimento repousa sobre uma mesa de ar horizontal. Um terceiro disco de mesma massa , desloca-se com atrito desprezível e velocidade sobre a mesa, perpendicularmente ao haltere, e colide frontalmente com o disco , ficando colado a ele.
(d) Determine a fração da energia mecânica inicial que é perdida no impacto.
Questão 108
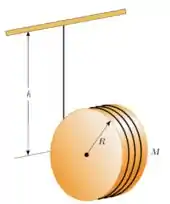
37. Um cilindro uniforme de raio e massa tem um fio enrolado sobre a sua superfície. O disco é solto do repouso com o fio vertical e com sua extremidade superior presa a uma barra fixa.
(d) Verifique a resposta anterior utilizando o enfoque da energia.
Questão 109
Uma mola, de comprimento natural e constante elástica , é montada no interior de um aro circular vertical de raio . Uma das extremidades da mola está fixa no ponto e a outra está livre no ponto mais baixo do aro. Um bloco de massa é empurrado contra a mola, que se desloca ao longo da curva em um arco de ângulo , até o ponto , como mostrado na figura. O bloco é então liberado, a partir do repouso. O atrito entre o bloco e o aro é desprezível. Adote o referencial da figura, com origem em .
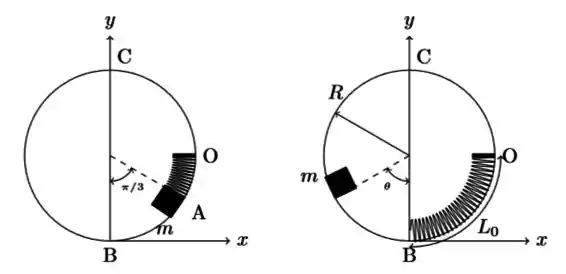
Obtenha uma expressão para a energia mecânica do bloco no ponto em termos de , , , e .
Determine o valor mínimo de para que o bloco consiga executar a curva completa, passando pelo ponto sem cair.
Sabendo-se que a partícula possui energia mecânica no ponto , obtenha uma expressão para a velocidade do bloco no trecho em função do ângulo , , , e .
Dado: , .
Ver solução completaQuestão 110
Um passeio de montanha-russa num parque de diversões parte do repouso a uma altura de acima do solo e rapidamente inicia a descida pelo trilho. Num certo momento, a pista faz um loop e o trem atinge uma uma altura de . Qual a velocidade do trem nesse momento, considerando que a carga completa do trem mais as pessoas sobre ele tem uma massa de ? (considere )
(a)
(b)
(c)
(d)
(e) s
Ver solução completaQuestão 111
Anna Ramalho 22/09 às 19h00
Conheça a montanha russa Chilli Beans do Rock in Rio
Jornal do Brasil
Anna Ramalho
Chilli Beans traz uma montanha russa para o Rock in Rio Apoiadora do Rock in Rio 2011, a Chilli Beans, deixa sua marca no evento com uma loja sustentável e uma montanha-russa assinada, aberta a todos os visitantes do festival.
O brinquedinho de metros de altura apresentará cenografia com o tema da campanha da Chilli Beanspara o Rock in Rio.
A capacidade da montanha russa é de pessoas, supondo a média da massa de cada pessoa igual a e o peso do carrinho de . A máxima velocidade apresentada pela montanha russa será:
Obs: Use o conceito de conservação de Energia Mecânica e concidere
(a) 42 m/s.
(b) 50 m/s.
(c) 29 m/s.
(d) 60 m/s.
(e) 19 m/s.
Ver solução completaQuestão 112
Uma conta de massa escorrega com atrito desprezível ao longo do arame mostrado na figura abaixo. Se a altura e a velocidade iniciais da conta são conhecidas, existem pelo menos dois métodos para encontrarmos o módulo da velocidade final da conta para uma dada altura final. São eles:
Resolver as leis de Newton para todas as forças do sistema;
Aplicar a conservação da Energia Mecânica.
Podemos então afirmar que:
O grau de dificuldade é o mesmo para os dois métodos, já que é necessário o conhecimento das forças que atuam na conta em ambos os casos.
É mais fácil resolver o problema utilizando Conservação da Energia Mecânica porque o movimento da conta depende da força aplicada pelo arame.
Como a velocidade da conta na altura final não depende da força aplicada pelo arame, então é mais fácil usar as Leis de Newton.
É mais fácil resolver o problema utilizando as Leis de Newton porque basta conhecer a aceleração para encontrarmos a velocidade.
É mais fácil resolver o problema utilizando Conservação de Energia Mecânica porque o módulo da velocidade na altura final não depende da força aplicada pelo arame.
Ver solução completaQuestão 113
Um pequeno bloco de massa é liberado em repouso de uma altura acima de uma superfície horizontal. A aceleração da gravidade é . O bloco desliza sem atrito sobre a parte interna de um trilho semicircular de raio . Qual das opções abaixo dá corretamente a rapidez do bloco e o módulo da força normal exercida sobre o bloco quando ele passa pelo ponto mais baixo do trilho?
(A) ;
(B) ;
(C) ;
(D) ;
(E) ;
Ver solução completaQuestão 114
Uma pequena esfera maciça é lançada verticalmente a partir do solo, num local de resistência do ar desprezível. O módulo da aceleração da gravidade é dado por . Considere a energia potencial gravitacional zero no solo. Sabendo que a altura máxima atingida pela esfera é , qual é o módulo de sua velocidade na altura em que sua energia cinética é igual a sua energia potencial gravitacional?
(a)
(b)
(c)
(d)
(e)
(f)
Ver solução completaQuestão 115
Na figura, um bloco de massa é solto do repouso em um plano inclinado sem atrito de ângulo . Abaixo do bloco há uma mola que pode ser comprimida por uma força de . O bloco para momentaneamente após comprimir a mola .
(a) Que distância o bloco desce ao longo do plano da posição de repouso inicial até o ponto em que para momentaneamente?
(b) Qual é a velocidade do bloco no momento em que entra em contato com a mola?
Questão 116
Uma esquiadora parte com velocidade inicial desprezível do topo de uma esfera de neve com raio muito grande e sem atrito, desloca-se diretamente para baixo (figura abaixo). Em que ponto ela perde contato com a esfera e voa seguindo a direção da tangente? Ou seja, no momento em que ela perde contato com a esfera, qual é o ângulo entre vertical e a linha que liga a esquiadora ao centro da esfera de neve?
Questão 117
Um bloco de massa m é empurrado contra uma mola de constante elástica k, e comprimento natural , por uma distância x, sendo mantido preso por um pequeno trinco. Quando o trinco é liberado, a mola expande-se empurrando o bloco. Ao passar pela posição de equilíbrio da mola, a mola perde contato com o bloco. O bloco segue adiante deslizando ao longo de uma superfície lisa e sem atrito, até passar a deslizar pelo interior de um aro circular de raio R. Sabendo que no ponto mais alto da trajetória dentro do aro o módulo da força do aro feita sobre o bloco (força normal) é igual a duas vezes o módulo da força peso do bloco. Suas respostas devem ser dadas em termos de m, , k, R e g:
a) Indique quais as forças que atuam sobre o bloco quando ele passa pelo ponto mais alto do aro.
b) Determine a velocidade do bloco no ponto mais alto da trajetória dentro do aro.
c) Determine a compressão inicial, x, da mola. Justifique claramente as Leis de Conservação utilizadas.
Ver solução completaQuestão 118
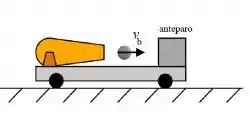
Um canhão é montado firmemente sobre um carrinho com rodas sem atrito, que está inicialmente em repouso em uma superfície horizontal lisa. O canhão dispara uma bala para a direita com uma velocidade , que é então capturada por um anteparo firmemente preso ao carrinho. Podemos afirmar que a velocidade final do sistema (constituído pelo carrinho+anteparo+canhão+bala) é:
- , para a esquerda.
- , para a direita.
- .
- , para a esquerda.
- , para a direita.
Questão 119
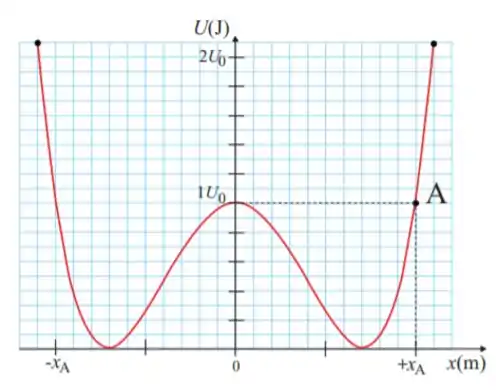
8. Uma partícula de massa move-se ao longo do eixo sob a ação de uma única força , conservativa, que dá origem à energia potencial mostrada no gráfico abaixo. Se a partícula passa pelo ponto A de coordenada com velocidade escalar , a sua velocidade escalar quando passa por um ponto de equilíbrio estável, em metros por segundo, é aproximadamente:
Questão 120
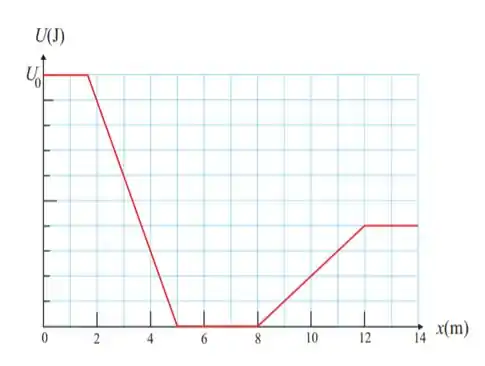
9. Uma partícula de massa move-se ao longo do eixo sob a ação de uma única força , conservativa, que dá origem à energia potencial representada na figura abaixo onde a escala no eixo é definida por . Se a partícula é liberada em com energia , a sua velocidade escalar, em , na posição , é:
Questão 122
Um projétil é lançado verticalmente da superfície da Terra com rapidez inicial de . Desprezando-se o atrito com o ar, a que altura acima da superfície da Terra ele chegará?
Dados:
Constante gravitacional:
Raio da Terra:
Massa da Terra:
Ver solução completaQuestão 123
Um bloco de massa e com velocidade inicial na parte horizontal do trajeto, sobe uma superfície circular sem atrito de raio .
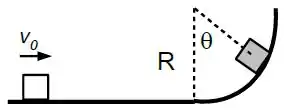
Dados:
a) Determine o módulo da velocidade do bloco na posição ilustrada na figura se .
b) Determine o valor da força normal que age no bloco nesta mesma posição.
Ver solução completaQuestão 124
Uma massa está suspensa no campo gravitacional por uma mola de constante elástica presa ao teto. Efeitos de atrito são desprezíveis e observa-se que o sistema oscila verticalmente em torno de sua posição de equilíbrio. A opção correta é:
- A energia mecânica do sistema não se conserva, pois alem da força gravitacional sobre a massa há, adicionalmente, a força elástica exercida pela mola.
- A energia mecânica do sistema se conserva, se considerarmos que esta é a soma das energias cinética e energia potencial gravitacional da massa.
- A energia mecânica do sistema se conserva, se considerarmos que esta é a soma das energias cinéticas e energia potencial elástica da mola.
- A energia potencial total, dada como a soma das contribuições de energia potencial gravitacional e energia potencial elástica, é conservada.
- A energia mecânica do sistema se conserva, se considerarmos que esta é a soma das energias cinética e das energias potencial gravitacional e potencial elástica da mola.
Questão 125
Um objeto de massa e dimensões desprezíveis parte do repouso e de uma altura , deslizando por uma rampa suave até encontrar uma superfície horizontal, por onde segue até encontrar uma rampa circular de raio , sobre a qual continua seu movimento (veja a figura). Não há atrito em todo o percurso do objeto, que se dá em um mesmo plano vertical (da figura). Expressando suas respostas em termos dos unitários horizontal e vertical indicados na figura, determine

- O vetor velocidade , nos pontos , e ;
- O vetor de força normal, , nos pontos , e .
Questão 126
Um vagão de 20 toneladas está freado no topo de uma descida. Em dado instante ele é solto, rola pela ladeira, descendo 9 m em relação à posição original. Na parte mais baixa da ladeira, ele engata em outro vagão, de 10 toneladas, que está livre nos trilhos. Os dois, engatados, sobem uma ladeira até uma altura H. Calcular H.
Ver solução completaQuestão 127
38. Uma roda cilíndrica de raio e massa , rola sem deslizar sobre um plano horizontal, deslocando-se com velocidade , e sobe sobre um plano inclinado de inclinação , continuando a rolar sem deslizamento. Até que altura o centro da roda subirá sobre o plano inclinado?
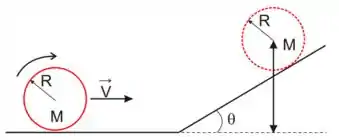
Questão 128
17. Uma bolinha de massa é colocada no canhão-de-mola como mostra a figura (abaixo à esquerda). Sabendo que a constante elástica da mola é e que sua compressão é de , responda:
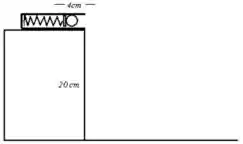
a) Qual a energia mecânica inicial da bolinha?
Ver solução completaQuestão 129
17. Uma bolinha de massa é colocada no canhão-de-mola como mostra a figura (abaixo à esquerda). Sabendo que a constante elástica da mola é e que sua compressão é de , responda:
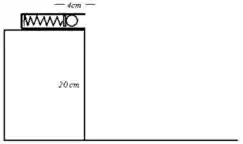
b) Qual a velocidade da bolinha quando ela chega à boca do canhão?
Ver solução completaQuestão 130
17. Uma bolinha de massa é colocada no canhão-de-mola como mostra a figura (abaixo à esquerda). Sabendo que a constante elástica da mola é e que sua compressão é de , responda:
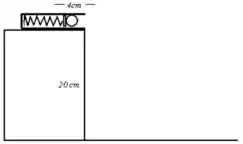
d) A velocidade da bolinha no instante imediatamente anterior ao choque com o solo.
Ver solução completaQuestão 131
17. Uma bolinha de massa é colocada no canhão-de-mola como mostra a figura (abaixo à esquerda). Sabendo que a constante elástica da mola é e que sua compressão é de , responda:
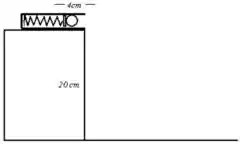
c) O tempo que a bolinha leva para alcançar o solo.
Ver solução completaQuestão 132
17. Uma bolinha de massa é colocada no canhão-de-mola como mostra a figura (abaixo à esquerda). Sabendo que a constante elástica da mola é e que sua compressão é de , responda:
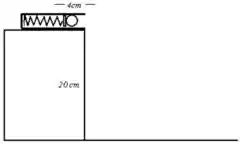
e) O ponto em que a bolinha toca o solo (sua posição quando chega no chão).
Ver solução completaQuestão 133
Uma partícula, inicialmente em repouso, desintegra-se em duas partículas idênticas, onde cada partícula possui massa de . Após a desintegração, a energia cinética total do sistema é de . Nesse processo, a porcentagem de massa da partícula inicial convertida em energia cinética foi de
a)
b)
c)
d)
Ver solução completaQuestão 134
Uma pistola de brinquedo dispara bolinhas plásticas utilizando um gatilho externo para movimentar uma mola de constante que se encontra em seu compartimento interno. Uma vez inserida uma bola de massa num extremo da mola, se aperta o gatilho produzindo uma compressão de na mola. Quando o gatilho é apertado até o limite, a mola volta à posição inicial imediatamente e a bolinha é solta adquirindo uma velocidade.
Considere as afirmativas:
I Quanto maior é a compressão da mola maior a velocidade adquirida pela bola.
II A velocidade com que a bola abandona a pistola depende de , e .
III Usando a mesma pistola, mas, trocando a bola plástica por uma bola de aço de igual tamanho e massa maior, a velocidade depois do disparo seria a mesma.
São verdadeiras:
(a) Apenas a I e a II
(b) Apenas a II.
(c) Apenas a III.
(d) Apenas a I.
(e) Nenhuma.
Ver solução completa