Filtros Polarizadores
Produzido por Bruno SoaresTeoria
Certos materiais afetam a polarização da luz
Em um filme 3D, a luz do telão sai com duas polarizações lineares em direções diferentes.
O efeito que vemos em 3D vem de como os óculos te permitem ver essas duas polarizações: uma das lentes apenas permite passar uma direção de vibração, e a outra só permite passar a segunda direção.
Outro exemplo de material que apenas permite a passagem de luz em uma direção são filtros de câmeras fotográficas.

Esses materiais que permitem a passagem apenas de luz com uma dada direção de polarização linear são chamados filtros polarizadoresou apenas polarizadores.
A direção que um polarizador permite passar é seu eixo de polarização.
Polarização Linear
A partir de agora, vamos supor que todos os polarizadoresque vamos analisar são ideais, ou seja, eles deixam passar da luz que é polarizada paralelamente ao eixo de polarização e bloqueia toda a luz que é polarizada perpendicularmente ao eixo de polarização.
Vamos começar um passo de cada vez. O que acontece quando luz não-polarizada atravessa um polarizador?
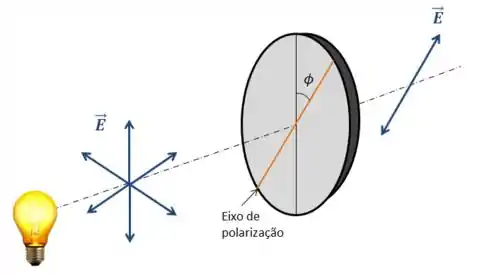
Quando uma luz não-polarizada incide sobre um polarizador ideal, a intensidade transmitida é exatamente a metade da intensidade da luz não-polarizada.
A explicação para isso é que podemos decompor o campo elétrico em uma componente paralela ao eixo de polarização e em uma componente perpendicular ao eixo de polarização, de forma que ambas sejam aproximadamente iguais.
O polarizador ideal deixa passar somente as componentes paralelas ao eixo de polarização, logo, metade da intensidade da luz que incide sobre o polarizador.
Dessa forma, a luz que entra vai ter módulo igual a soma vetorial dessas duas componentes (Pitágoras):
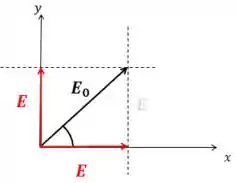
Assim, como apenas uma das duas passa pelo filtro e a intensidade varia com o quadrado do campo elétrico, a fração da intensidade incidente que vai ser transmitida é:
Agora vamos para o segundo caso:
Luz linearmente polarizada atravessando um polarizador.
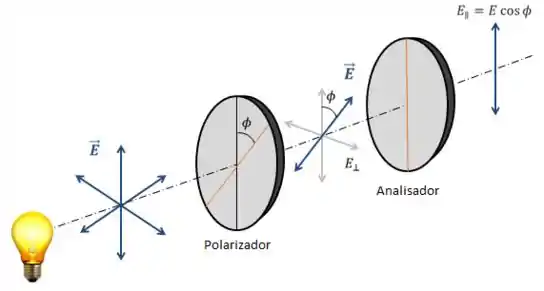
Usamos um primeiro polarizador pra podermos conseguir nossa luz linearmente polarizada.
O que nos importa é o segundo. Chamamos o segundo polarizador de analisador. Agora, a luz sofrerá duas polarizações, conforme ilustra a figura acima.
Neste caso, a intensidade da luz que emerge do analisador é dada pela Lei de Malus.
Onde é a intensidade máxima da luz transmitida (que é igual à luz incidente naquele polarizador) e é a intensidade transmitida para certo ângulo .
A ideia é a mesma da luz não polarizada: dividimos a luz incidente em uma componente perpendicular ao eixo de polarização do analisador e uma componente paralela
Como a intensidade depende do quadrado do campo elétrico, nós elevamos isso ao quadrado.
Polarizadores em sequência
No caso de termos vários polarizadores um depois do outro, apenas precisamos usar a Lei de Malus várias vezes seguidas.
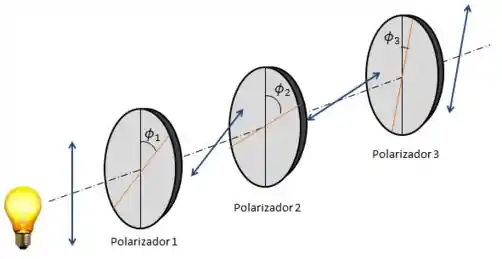
Na nossa imagem, a intensidade que sai do polarizador 1 será:
Já a do polarizador 2 vai ser:
E para o polarizador 3:
Se juntarmos tudo:
Tem dois detalhes importantes pra lembrarmos ao fazer isso.
Quando a luz atravessa um polarizador, nós temos que usar o ângulo entre a polarização da luz e o eixo de polarização.
Lembrando que a luz que emerge do filtro vibra na direção do seu eixo, o ângulo entre ela e o polarizador seguinte vai ser igual ao ângulo entre os dois eixos.
O segundo ponto importante é que a intensidade do lado direito da equação é a da luz que atinge o filtro. Note que apenas no primeiro filtro temos do lado direito, a intensidade da luz original.
A intensidade que atinge o polarizador 2 é , e a que atinge o 3 é .
Outra possibilidade é que a luz que atinge o polarizador 1 seja não polarizada. Neste caso:
E essa intensidade não depende do ângulo do polarizador!
Mas o resto continua igual.
Gráficos da Rotação de Polarizadores
Como ficaria a intensidade caso fôssemos mudando esse ângulo? Bem, a resposta nós já sabemos: ela varia com o cosseno ao quadrado do ângulo!
O gráfico fica:
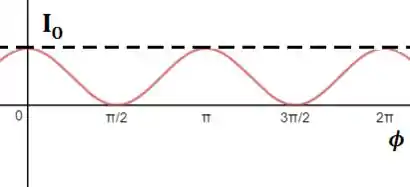
Desse gráfico podemos obter uma série de informações.
- A intensidade inicial (que é o valor máximo no gráfico)
- Sabendo podemos ver a diferença de ângulos
Simbora pros exercícios?