Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Polarização da Luz

Ver Todos os Exercícios

Teoria

Fala aí! Seja bem vindo ao Responde Aí! Bora aprender sobre Polarização da luz?!

O que é Polarização da Luz?

A polarização é uma característica de todas as ondas eletromagnéticas, e como a luz é uma onda, ela não fica de fora!

Luz polarizada e não polarizada
Luz polarizada e não polarizada

Resumindo bastante, uma luz não polarizada é aquela que vai pra todas as direções! A maior parte das fontes de luz que temos no nosso dia a dia é não polarizada, como por exemplo a luz do sol, ou até a lâmpada da sua casa!

Já a luz polarizada se propaga em uma direção só e pra conseguirmos uma que a luz tenha esse comportamento, podemos passar ela em filtros polarizadores. Mas isso já é assunto pra um outro momento! 😉

📢 Clique para ver mais:

Tipos de polarização da luz

A polarização da luz pode ser linear, circular ou elíptica, isso acontece por que o campo elétrico fica mudando de direção, de forma a descrever uma reta, uma circunferência ou uma elipse!

Se liga nesse exemplo aqui:

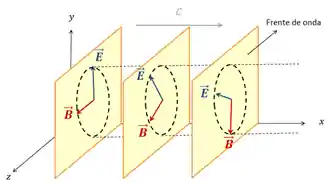
Onda se propagando na direção x
Onda se propagando na direção x


Temos uma onda se propagando na direção e o campo elétrico formado tem duas componentes, uma no eixo e outra no eixo . Ela segue essa equação aqui:

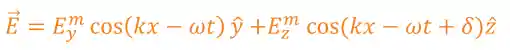
Polarização da onda: Equação
Polarização da onda: Equação

A polarização da onda depende dessa defasagem entre as duas componentes e suas amplitudes, e .

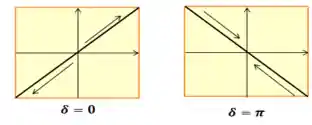
  • Quando ou , a polarização é linear, independente das amplitudes.
  • Quando e amplitudes forem iguais, a polarização é circular.

A polarização elíptica é um caso mais geral, e acontece quando:

  • for diferente de ou e as amplitudes forem diferentes;
  • for diferente de , ou e as amplitudes forem iguais.

Quer aprender mais sobre luz polarizada?! Então confere esse vídeo iradoso! 👇

Polarização linear

No caso da polarização linear, vamos imaginar uma onda qualquer se propagando em :

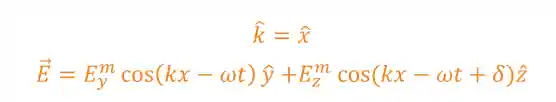
Onda se propagando em x.
Onda se propagando em x.

A amplitude da nossa onda vai levar em conta a amplitude em e a amplitude em :

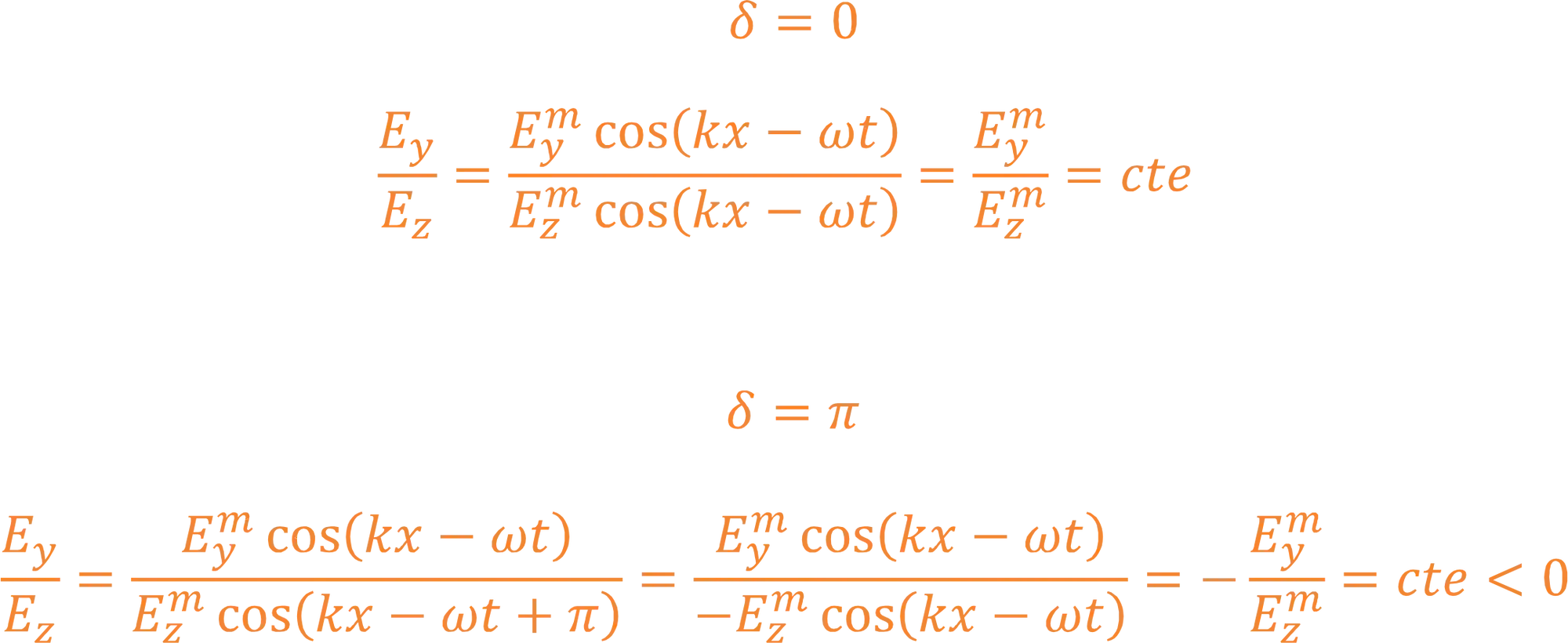
Polarização linear da luz: Equações
Polarização linear da luz: Equações

Como podemos ver acima, sempre que a gente tiver uma polarização linear, a razão entre as amplitudes dos eixos e , vão ser constantes. Sabendo disso, podemos desenhar os seguintes gráficos para um caso geral:

Polarização linear da luz: Gráficos
Polarização linear da luz: Gráficos

Polarização Elíptica

Agora, e se a gente tiver se deparar com ou !? A gente vai cair nesse tipo de equação aqui:

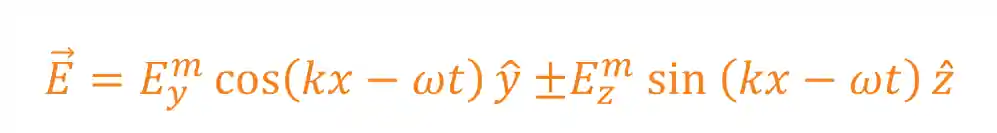
Equação da luz polarizada na forma elíptica
Equação da luz polarizada na forma elíptica

Repara que a equação acima tem um formato muito parecido com a equação da elipse:

Isso significa que nosso campo magnético vai ter um formato elíptico, logo vamos ter uma polarização elíptica!

O gráfico da polarização elíptica vai ter essa carinha aqui:

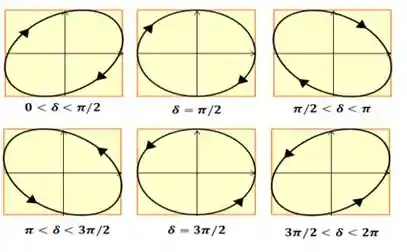
Polarização Elíptica: Gráfico
Polarização Elíptica: Gráfico

Polarização Circular

A polarização circular da luz é um caso especial da polarização elíptica, quando . Nesse caso o nosso gráfico fica com essa carinha aqui:

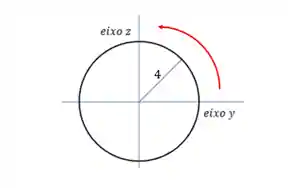
Polarização Circular da Luz: Gráfico
Polarização Circular da Luz: Gráfico

Maneiro, não é!? Agora vamos praticar com exercícios?!

Polarização linear

Polarização Elíptica

Polarização Circular

Exercícios Resolvidos

Exercício Resolvido #1

Halliday, Resnick, Jearl Walker, Fundamentos de física, volume 4: Óptica e Física Moderna, 8ª ed. Rio de Janeiro: LTC, 2009, pp 37-89, modificado

A componente magnética de uma onda luminosa polarizada é dada por

B x = 4,0 × 10 - 6 T sen ⁡ 1,57 × 10 7   m - 1 y + ω t

Determine:

  1. A direção de polarização da luz.
  2. A frequência da luz.

Passo 1

Letra a)

Como o campo magnético depende apenas de y , sabemos que essa onda se propaga ao longo do eixo y embora não saibamos em que sentido.

A componente magnética é ao longo do eixo x .

Como a componente elétrica tem de ser perpendicular tanto a B → quando a direção de propagação, ela tem de ser perpendicular aos eixos x e y .

Para isso, a componente elétrica tem de estar ao longo do eixo z . Como a direção de polarização é a direção de vibração da componente elétrica, essa onda é polarizada na direção do   e i x o   z .

Passo 2

Letra b)

O número da onda é dado no enunciado, dentro da função seno.

k = 1,57 ∙ 10 7   m - 1

Junto com a frequência angular ele nos dá a velocidade da luz, que é uma constante conhecida c = 3 ∙ 10 8   m / s .

ω k = c

ω = c ∙ k = 3 ∙ 10 8 ∙ ( 1,57 ∙ 10 7 )

Conhecemos também a relação entre a frequência angular e a frequência:

ω = 2 π f

f = ω 2 π = 3 ∙ 10 8 ∙ 1,57 ∙ 10 7 2 π ≅ 7,50 ∙ 10 14 H z

Resposta

Letra a)

A polarização é paralela ao e i x o   z

Letra b)

f ≅ 7,50 ∙ 10 14 H z

Exercício Resolvido #2

Halliday, Resnick, Jearl Walker, Fundamentos de física, volume 4: Óptica e Física Moderna, 8ª ed. Rio de Janeiro: LTC, 2009, pp 38-99, modificado

A componente magnética de uma onda polarizada é dada por B x = 4,00 μ T sen ⁡ k y + 2,00 × 10 1 5   s - 1 t . Determine:

  1. A direção de propagação da onda.
  2. A direção de polarização da luz.
  3. Escreva uma expressão para o campo elétrico da onda, incluindo o valor do número de onda.
  4. Determine o comprimento de onda.
  5. Em que região do espectro eletromagnético está essa onda?

Passo 1

Letra a)

A componente magnética da onda varia apenas ao longo do e i x o   y .

Isso significa que a onda se propaga na direção do e i x o   y .

Se seguirmos a frente de onda temos que ter k y + ω t = c o n s t a n t e . Quando o tempo passa, para essa relação continuar constante, o valor de y tem de diminuir.

Logo, a onda se propaga no sentido negativo do e i x o   y .

Passo 2

Letra b)

A direção de polarização da luz é a direção de vibração do campo elétrico.

O campo magnético no enunciado vibra ao longo do e i x o   x ( B = B x ), e a onda se propaga ao longo do e i x o   y . Como o campo elétrico tem de ser perpendicular a essas duas direções, ele vai vibrar ao longo do e i x o   z .

Logo, a luz é polarizada ao longo do e i x o   z .

Passo 3

Letra c)

Como já temos o campo magnético, nós usamos a relação entre ele e o campo elétrico:

E = c B

Logo:

E = c ∙ 4,00 μ T sen ⁡ k y + 2,00 ∙ 10 1 5   s - 1 t

Multiplicando c = 3 ∙ 10 8 pela amplitude B m = 4,00 μ T = 4,00 ∙ 10 - 6 T :

E m = c ∙ 4,00 ∙ 10 - 6 = 3 ∙ 10 8 ∙ 4 ∙ 10 - 6 = 1200   V / m

Mas o exercício também nos pede para encontrar o número de onda. Para isso, ele nos deu a frequência angular ω = 2,00 ∙ 10 5   s - 1 , sendo que nós já sabemos a velocidade da luz e a relação entre essas três grandezas:

ω k = c

k = ω c = 2,00 ∙ 10 1 5 3 ∙ 10 8 ≅ 6,67 ∙ 10 6   m - 1

Temos então:

E z = 1200   V / m sen ⁡ 6,67 ∙ 10 6   m - 1 y + 2,00 ∙ 10 1 5   s - 1 t

Passo 4

Letra d)

O comprimento da onda é dado pelo número de onda.

k = 2 π λ

λ = 2 π k = 2 π 6,67 ∙ 10 6 ≅ 0,942 ∙ 10 - 6   m = 942   n m

Passo 5

Letra e)

A frequência da onda é dada por:

λ f = c

f = c λ = 3 ∙ 10 8 942 ∙ 10 - 9 = 3,184713 ∙ 10 14 H z

Que está entre a região do infravermelho e da luz visível. Neste caso, precisamos consultar alguma fonte do espectro com bastante precisão para confirmar a região na qual essa onda se encontra.

Em geral, imagens do espectro eletromagnético também mostram o espectro em função do comprimento de onda e neste caso podemos ter certeza que estamos fora da região do visível, que vai de aproximadamente 400   n m (luz violeta) a 750   n m (luz vermelha).

Para este valor, ela está na região do infravermelho.

Resposta

Letra a)

A onda se propaga ao longo do e i x o   y no sentido negativo do eixo.

Letra b)

A luz é polarizada ao longo do e i x o   z .

Letra c)

E z = 1200   V / m sen ⁡ 6,67 ∙ 10 6   m - 1 y + 2,00 ∙ 10 15   s - 1 t

Letra d)

λ ≅ 942   n m

Letra e)

Essa onda está na região do infravermelho.

Exercício Resolvido #3

PUC-RIO, Física 4, Prova 1, 2013.2

Obtenha a polarização da onda eletromagnética representada abaixo. Demonstre o tipo de polarização (linear, circular ou elíptica) e mostre, caso não seja linear, se a polarização é à esquerda ou à direita. Use a técnica vetorial usada em aula:

E z x , t = E z m . sen ⁡ k . x - ω . t ;  

E y x , t = E y m . cos ⁡ ( k . x - ω . t + π )

onde E z m ≠ E y m .

Passo 1

Para determinar o tipo de polarização, precisamos avaliar se as componentes do vetor campo elétrico tem a mesma amplitude e precisamos também determinar se há diferença de fase entre as componentes, e de quanto é essa diferença.

Passo 2

Para vermos a diferença de fase das duas componentes do campo elétrico, o melhor é escrevermos elas como uma mesma função trigonométrica. A trigonometria nos diz que:

cos ⁡ a ± b = cos ⁡ a cos ⁡ b ∓ sen ⁡ b sen ⁡ a

Se b = π / 2 , temos:

cos ⁡ a + π 2 = - sen ⁡ a

s e n a = - cos ⁡ a + π 2

Como a compontente z tem um seno podemos rescrever essa parte como

E z x , t = E z m . sen ⁡ ( k . x - ω . t ) = - E z m cos ⁡ k x - ω t + π 2

Assim:

E y x , t = E y m . cos ⁡ ( k . x - ω . t + π )

E z x , t = - E z m cos ⁡ k x - ω t + π 2

Agora dá pra comparar! A diferença de fase vai ser:

δ = k x - ω t + π - k x - ω t + π 2 = π 2

A polarização será circular ou será elíptica.

Passo 3

Para determinar se a polarização é circular ou elíptica, devemos avaliar se as amplitudes de cada componente são iguais ou diferentes. Pela informação dada, vemos que as amplitudes são diferentes, pois:

E z m ≠ E y m

Então temos uma polarização elíptica

Passo 4

Para determinar o sentido da polarização, precisamos calcular o vetor campo elétrico, que é a soma das componentes, para dois instantes no tempo, para t 1 = 0 e para t 2 = T / 4 , do ponto de observação x = 0 . Sabendo que ω = 2 . π T , temos que T = 2 . π ω , ou seja, t 2 = π 2 . ω .

Para x = 0 e t = 0 , temos:

E z x , t = - E z m . cos ⁡ k . x - ω . t + π 2

E z 0,0 = - E z m . cos ⁡ k . 0 - ω . 0 + π 2 = 0

E y x , t = E y m . cos ⁡ ( k . x - ω . t + π )

E y 0,0 = E y m . cos ⁡ ( k . 0 - ω . 0 + π ) = - E y m

Ou seja, para x = 0 e t = 0 , temos que o vetor campo elétrico é:

E → = - E y m ( j ^ )

Para x = 0 e t = π 2 ω , temos:

E z x , t = - E z m . cos ⁡ k . x - ω . t + π 2

E z 0 , π 2 ω = - E z m . cos ⁡ k . 0 - ω . π 2 ω + π 2 = - E z m cos ⁡ 0 - π 2 + π 2

E z 0 , π 2 ω = - E z m

E y x , t = E y m . cos ⁡ ( k . x - ω . t + π )

E y 0 , π 2 ω = E y m . cos ⁡ ( k . 0 - ω . π 2 ω + π ) = E y m cos ⁡ ( 0 - π 2 + π )

E y 0,0 = 0

Ou seja, para x = 0 e t = π 2 ω , temos que o vetor campo elétrico é:

E → = - E z m ( k ^ )

Passo 5

Para determinar a direção do giro vamos fazer um desenho do campo elétrico em x = 0 nos dois tempos que calculamos acima, ou seja

E → ( 0 ,   0 ) = - E y m ( j ^ )

E → 0 , T 4 = - E z m ( k ^ )

Aqui eu supus E z m < E y m , mas podia ser o contrário!

Como a onda está se propagando na direção i ^ (pois o argumento do lá das funções trigonométricas é k x - ω t ), então para um observador que vê a onda vir na sua direção a direção da polarização é anti-horária como tá no nosso desenho!

Resposta

A polarização é elíptica e, para um observador que vê a onda vir na sua direção, a direção da polarização é anti-horária.

Exercícios de Livros Relacionados

Qual é o ângulo de polarização para a luz no ar que incide a na água n = 1,33 b no vidro n = 1,50
Demonstre que os vetores de polarização circular (5.39) formam uma base ortonormal para um produto escalar de vetores complexos a → e b → definido como a → * ∙ b → , ou seja, que ε ^ + * ∙ ε ^ - = ε ^
Demonstre, para o caso geral de polarização elíptica (5.29), que o ângulo ψ entre o eixo maior da elipse de polarização e o eixo O x é dado por (fig.) tan ⁡ 2 ψ = tan ⁡ 2 α cos ⁡ δ Onde tan ⁡ α ≡ b /
Na praia, a luz em geral é parciahnente polarizada devido às reflexões na areia e na água. Em uma certa praia, em um certo dia, no final da tarde, a componente horizontal do vetor campoelétrico é 2,3
O ângulo crítico para a reflexão interna total para uma substância é 48 ° . Qual é o ângulo de polarização para a substância?