Efeito Doppler
Produzido por Leonardo de BemTeoria
O que é isso?
Vamos entender a ideia: você já reparou que a sirene de uma ambulância parece ficar mais grave à medida que ela se afasta de nós, certo!? Esse é o exemplo clássico de efeito Doppler.
O efeito Doppler é justamente isso: o som de uma fonte sonora (sirene, por exemplo) ficar mais grave à medida que se afasta do observador ou mais agudo à medida que se aproxima do observador.
Como calcular?
O que acontece é o seguinte: a fonte está emitindo um som com uma frequência e o observador escuta um som com frequência Elas se relacionam por:
onde:
é a freqüência ouvida pelo observador
é a freqüência da fonte sonora
é a velocidade do som no meio (ar, em geral)
é a velocidade do observador
é a velocidade da fonte
Quando usamos sinal de ou de ?
Simples! Usaremos sempre o referencial que vai do observador até a fonte. Essa direção será considerada positiva. O sentido contrário é considerado negativo:
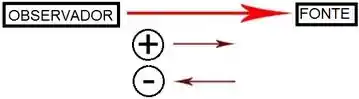
Vamos ver um exemplo pra entender melhor?
Imagina um carro buzinando indo em direção ao outro:

Vamos supor que é o carro azul que está buzinando e que o observador está no carro vermelho.
O primeiro passo é definir a direção positiva, que vai sempre do observador em direção à fonte.
Nesse caso, a fonte é o carro azul e o observador é o carro vermelho.
Então:
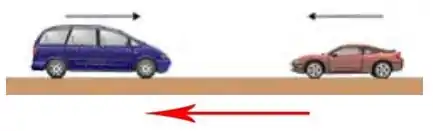
Pronto! Definimos a direção positiva.
Assim, podemos perceber que a velocidade da fonte (carro azul) é negativa e a velocidade do observador é positiva, de acordo com nosso referencial.
Então a fórmula, nesse caso, fica assim:
Só isso! Depois, é só calcular e substituir os dados que o problema fornecer.
Efeito Doppler em mais de uma dimensão
Até agora vimos o efeito Doppler ocorrer em situações onde a fonte e/ou o observador se movem em um único eixo, certo?
Então, e se tivermos uma situação de mais de uma dimensão? Como fazemos?
Simples! A ideia é sempre decompor as velocidades na direção da reta que liga o observador e a fonte e aplicar fórmula do efeito Doppler.
Efeito Doppler Envolvendo Vento
Vamos complicar mais um pouquinho?
Até agora aplicamos a fórmula do efeito Doppler sempre considerando a velocidade do som uma constante igual a . Mas existe algo que possa alterar esse valor?
A resposta é sim. O vento é capaz de alterar o valor da velocidade do som. Mas como???
Calma, amigo, vou te explicar. É assim:
- Quando a propagação do som tem sentido contrário à velocidade do vento, consideramos:
- Quando a propagação do som tem sentido igual à velocidade do vento, consideramos:
Viu como funciona nesse caso? Show.
Efeito Doppler Envolvendo Reflexão
Esse é mais um dos casos especiais para o uso do efeito Doppler. No entanto, esse exemplo aparece MUITO. Então se liga, que aqui no Responde Aí você vai ficar craque rapidinho.
Vamos usar um exemplo pra facilitar. Confia que vai dar certo!
Um carro possui uma sirene que soa com frequência . Determine a frequência percebida pelo motorista ao se aproximar de parede com velocidade .
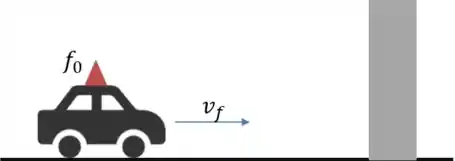
Bem, o enunciado fica meio estranho se você for analisar com cuidado. Como o motorista está em repouso em relação à sirene, podemos concluir que a frequência percebida por ele é igual a , certo? Então, essa resposta não está errada, mas é inconveniente. O objetivo da questão é, obviamente, saber a frequência percebida originada da reflexão das ondas na parede.
Então vamos lá.
A primeira coisa a se fazer é considerar que a parede é um observador fixo e ele receberá uma frequência diferente de , já que o carro está se movendo, então:
Onde é a velocidade do som.
Mas sabemos que a parede vai rebater tudo que chegar nela sem alterar a frequência. O que podemos concluir com isso? A parede se tornará uma nova fonte com frequência .
Agora temos um novo problema. Uma fonte fixa de frequência com um observador se aproximando com velocidade . Logo:
Substituindo o valor de :
Se ligou? Usando esse método de uma “fonte imaginária” não tem erro.
Nos exercícios você vai ver todas as possíveis variações desse problema. Bora praticar!
Quando usamos sinal de + ou de - ?
Efeito Doppler em mais de uma dimensão
Efeito Doppler Envolvendo Vento
Efeito Doppler Envolvendo Reflexão
Exercícios Resolvidos
Exercício Resolvido #1
Halliday, David, Fundamentos de física, volume 2 : ondas, 8 ed. Rio de Janeiro : TLC, 2008, Cap 17, Problema 37
Num dia em que a velocidade do som é , um amigo seu canta em voz alta, emitindo uma única nota de enquanto corre em sua direção a .
Que frequência você escuta?
Que frequência o seu amigo ouviria se você subitamente começasse também a emitir uma nota musical de ?
Passo 1
Quando temos uma fonte sonora que está se movimentando, temos logo que pensar em Efeito Doppler:
Onde é a frequência ouvida pelo observador, é a frequência da fonte sonora, é a velocidade do som, é a velocidade do observador e é a velocidade da fonte!
Vamos reunir os dados que temos:
Lembrando que o sentido positivo vai do observador para a fonte. Logo, terá um sinal de antes.
Substituindo os valores, temos:
Passo 2
Nesse caso, temos que o observador passa a ser o amigo, nesse caso, temos:
Substituindo na fórmula, temos:
Resposta
Exercício Resolvido #2
Halliday, David, Fundamentos de física, volume 2 : ondas, 8 ed. Rio de Janeiro : TLC, 2008, Cap 17, Problema 56
Uma ambulância cuja sirene emite um som com uma frequência de passa por um ciclista que está a . Depois de ser ultrapassado, o ciclista escuta uma frequência de . Qual é a velocidade da ambulância?
Passo 1
Como foi dito, a ambulância ultrapassou o ciclista, portanto, temos que a ambulância (fonte) está se distanciando com velocidade do ciclista (observador), que, por sua vez, está tentando se aproximar da ambulância com velocidade .
Como todas as velocidades têm o mesmo sentido, que é do observador para a fonte, usaremos só o sinal de .
Substituindo na fórmula do efeito Doppler e usando :
Como , a frequência da sirene é e , a frequência percebida vale :
Resposta
Exercício Resolvido #3
UFRJ-PF-2014.2-3
Considere um carro movendo-se com velocidade em direção a uma parede, conforme a figura. O carro tem uma sirene, que está ligada, e emite som de frequência . Um observador parado, junto à parede, recebe as ondas sonoras e mede uma frequência . As ondas refletidas pela parede são recebidas pelo motorista do carro, que mede uma frequência . Marque a alternativa correta:
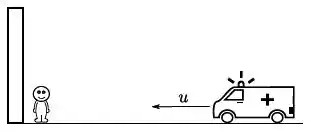
Passo 1
Vamos usar a fórmula:
Do Efeito Doppler. Bom, como no primeiro caso temos uma fonte que se aproxima de um observador, a equação vai ficar assim:
Passo 2
No segundo caso, a gente passa a considerar a parede como uma nova emissora de ondas e o carro como observador.
Nesse caso a fonte está imóvel e o observador em movimento.
Só que, nesse caso, a frequência da fonte, que é a parede, é igual a frequência
Passo 3
Unindo as duas inequações:
b)
Resposta
b)
Exercício Resolvido #4
UNICAMP-Questão 4 - P2.2012 (Noturno)
Um morcego está voando em uma caverna, orientando-se através de pulsos ultrassônicos. A frequência do som emitido pelo morcego é . O morcego aproxima-se de uma parede plana da caverna com uma velocidade igual a vezes a velocidade do som no ar. Qual é a frequência com que o morcego ouve o som refletido pela parede da caverna?
Dado:
Passo 1
Primeiro vamos calcular a frequência que chega na parede e que seria sentida por um observador que lá estivesse:
Nesse caso o morcego é a fonte e a parede o observador:
Passo 2
Agora vamos considerar a parede como a nova fonte de ondas e o morcego como o observador. Logo: .:
É essa a frequência que procurávamos (:.
Resposta
Exercício Resolvido #5
Halliday, David, Fundamentos de física, volume 2 : ondas, 8 ed. Rio de Janeiro : TLC, 2008, Cap 17, Problema 66
Dois trens viajam um em direção ao outro a em relação ao solo. Um dos trens faz soar um apito de . (a) Que frequência é ouvida no outro trem se o ar está parado? (b) Que frequência é ouvida no outro trem se o vento está soprando a no sentido contrário ao do trem que apitou? (c) Que frequência é ouvida se o sentido do vento se inverte?
Passo 1
a) Os trens estão se aproximando, tanto a fonte como o observador, então:
Sendo:
Passo 2
b) Aqui, com o vento, temos somente uma variação na velocidade do som , como o vento é contrário à velocidade do som, e a velocidade do observador é arbitrariamente definida como positiva, temos que, a nova velocidade do som é dada por:
Portanto:
Passo 3
c) Se o vento se inverte, temos que a nova velocidade do som é:
E então:
Resposta
a)
b)
c)
Exercício Resolvido #6
Halliday, David, Fundamentos de física, volume 2 : ondas, 8 ed. Rio de Janeiro : TLC, 2008, Cap 17, Problema 67
Uma sirene de e um funcionário da defesa civil estão em repouso em relação ao solo. Que frequência o funcionário ouve se o vento está soprando a (a) da fonte para o funcionário e (b) do funcionário para a fonte?
Passo 1
a) Com o vento soprando em direção ao funcionário, a nova velocidade do som é dada por:
É isso aí! Não há efeito Doppler!
Então se liga, sempre que não houver movimento relativo entre fonte e observador, o efeito Doppler não ocorre!
Passo 2
Continuamos sem movimento relativo entre fonte e observador. Nesse caso a única coisa que mudaria seria a expressão de :
Mas, quando jogarmos na fórmula de Doppler:
Resposta
Exercício Resolvido #7
Halliday, David, Fundamentos de física, volume 2 : ondas, 8 ed. Rio de Janeiro : TLC, 2008, Cap 17, Problema 57
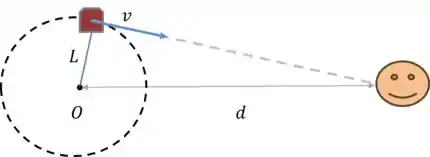
Um apito de se move em uma circunferência com de raio com uma velocidade angular de . Quais são as frequências (a) mais baixa e (b) mais alta escutadas por um ouvinte distante, em repouso em relação ao centro da circunferência?
Passo 1
A primeira coisa aqui é a gente fazer um desenho dessa situação:
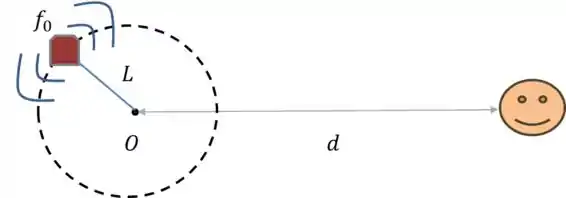
No movimento circular, a velocidade nem sempre vai estar na mesma direção da reta entre o observador e a sirene, certo? Nesses casos, como a gente viu lá na teoria, o que a gente tem que fazer é decompor a velocidade na direção da reta.
Mas calma! Como nos foi pedido as frequências extremas, não precisamos pensar nesses casos. Vamos só considerar os casos em que a velocidade tem a direção da reta que liga a sirene ao observador.
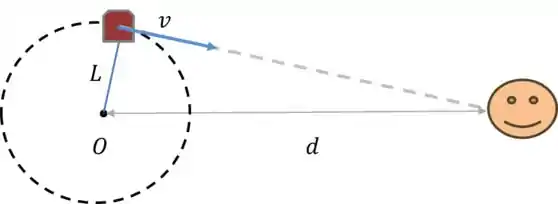
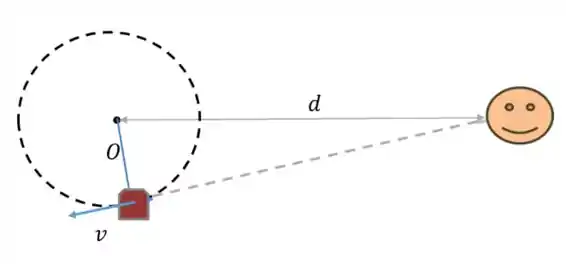
Passo 2
- Vamos ter a frequência mínima quando o apito estiver se afastando da fonte:
- Já para a frequência máxima, o apito estará se aproximando:
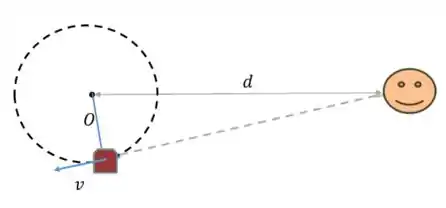
Sabemos também que:
Como a frequência do apito é e a velocidade do som é :
Passo 3
Os valores da frequência e da velocidade do som são os mesmos:
Resposta
Exercício Resolvido #8
Halliday, David, Fundamentos de física, volume 2 : ondas, 8 ed. Rio de Janeiro : TLC, 2008, Cap 17, Problema 60
Uma fonte sonora e uma superfície refletora se movem uma em direção à outra. Em relação ao ar, a velocidade da fonte é , a velocidade da superfície é e a velocidade do som . Aa fonte emite ondas com uma frequência de no referencial da fonte. No referencial do refletor, quais são (a) a frequência e (b) o comprimento de onda das ondas sonoras? No referencial da fonte, quais são (c) a frequência e (d) o comprimento de onda das ondas sonoras refletidas de volta para a fonte?
Passo 1
a) Temos que considerar aqui a superfície como um observador simples, portanto, aplicando a fórmula do efeito Doppler, temos:
Substituindo os valores:
Passo 2
b) Se usarmos a relação
Obtemos o valor do comprimento de onda:
Passo 3
c) Agora vamos considerar a superfície refletora como uma fonte com frequência igual à essa que encontramos na letra (a), e aplicar novamente a fórmula do efeito Doppler:
Mas é importante lembrar que:
- agora é a frequência que chega na superfície:
- é a velocidade da fonte sonora, já que agora queremos a frequência que chega na fonte após a reflexão
- é a velocidade da superfície
Substituindo os valores:
Passo 4
d) Se usarmos a relação
Obtemos o valor do comprimento de onda:
Resposta
Exercício Resolvido #9
UFRJ-P2-2015.1-7
Uma fonte sonora em repouso faz-se ouvir por dois observadores, e , também em repouso. A partir de um certo momento, esta fonte começa a se mover com velocidade constante. A figura abaixo mostra e e as frentes de ondas produzidas por em repouso, à esquerda, e em movimento, à direita. Sobre a segunda situação, assinale a alternativa CORRETA:
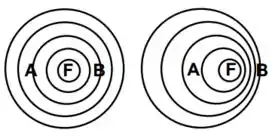
- A fonte F se move pra esquerda.
- O período de onda parece maior para
- e observam o mesmo comprimento de onda.
- A velocidade de propagação das ondas depende da direção de observação.
- observará um comprimento de onda maior que
Passo 1
E aí, galera, como devemos interpretar fisicamente isso?
Bom, ali existe uma fonte , se deslocando para a direita. Como eu sei isso? Porque, como nós vimos no capítulo, as ondas ficam mais “acumuladas” na ponta do deslocamento.
Como assim? Bom, se a fonte está indo pra direita, as ondas vão ficar mais acumuladas na direita e mais espaçadas na esquerda, e vice-versa.
Passo 2
Show, mas então, quais serão as frequências percebidas por e em relação à frequência original?
Seja a frequência da fonte.
Como a fonte está se aproximando de , e é ali que acontece o “acúmulo”, a frequência percebida por será maior:
E, já que a fonte está se afastando de , a frequência percebida por será menor:
Assim:
Passo 3
Daí, usando a equação:
Assim, quanto maior a frequência, menor o comprimento de onda. Então podemos reescrever a inequação anterior assim:
Só do que a gente falou aqui, podemos excluir as seguintes letras:
Letra a) A fonte se move pra direita.
Letra b) Na verdade, como a maior frequência percebida é , e:
Então, o menor período percebido será o de
Letra c) Não faz sentido por causa do próprio efeito Doppler
Letra d) Não depende, se propaga para todas as direções na forma de circulo, como mostra a figura.
No caso, a correta então é a letra e, pois:
Resposta
e)
Exercício Resolvido #10
USP-P3-2010-Q3
Um submarino (sub A), navegando a uma velocidade , envia um sinal de sonar (onda sonora na água) com frequência . O sinal é refletido pelo casco do submarino inimigo(sub B)que viaja com uma velocidade na direção oposta(vide figura). Considere a velocidade do som na água como sendo e despreze quaisquer efeitos de interferência.

- Se a frequência do sinal medido pelo submarino é , qual a velocidade
- Qual a frequência do sinal refletido, medido pelo submarino
- Nesse caso, qual será a frequência do sinal “falso” medido pelo submarino
- Se os engenheiros do submarino forem de fato enganados e pensarem que esse sinal éa reflexão do sinal original, que valor obterão pra velocidade (e direção) do submarino
Considere que o submarino seja dotado de um sistema contra-medidas que (1)suprime completamente o sinal enviado pelo Sub A, (2)altera a velocidade do submarino pra , e (3)envia um outro sinal de sonar(sinal “falso” ) com frequência , com o intuito de confundir o inimigo.
Passo 1
a):
Esse é um caso comum de efeito Doppler. Nesse caso, sub A é a fonte e sub B o observador e ambos se aproximam.
Vamos aplicar a equação do efeito Doppler então:
Lembrando que: como o observador se aproxima, colocamos o “+” no numerador e como a fonte se aproxima, o “-“ no denominador.
A nossa incógnita é o .
Vamos isolar ele:
Beleza!
Vamos aplicar os valores que temos do enunciado:
Passo 2
b):
Agora os papéis se invertem. Você lembra como faz esse tipo de questão quando há uma reflexão em um corpo? O corpo que reflete as ondas se torna a nova fonte de ondas.
Por causa disso, vamos considerar agora que o sub B é a fonte e o sub A é o observador, e ambos se aproximam. Por que ambos se aproximam, você já sabe, mais encima e menos embaixo:
Então:
Passo 3
c):
Bom, como vamos pensar nesse item?
Seguinte:
Aqui o sub B não reflete mais a onda verdadeira mandada pelo sub A. O que acontece agora é que o sub B passa a se comportar como uma fonte se movendo à , se aproximando do observador, e emitindo uma frequência de . Então, vamos aplicar a fórmula do efeito Doppler pra essa “fonte” e pro observador(Sub A):
Passo 4
d):
Bom, se os engenheiros forem enganados mesmo, eles acharão que o que aconteceu foi uma simples reflexão. Ou seja, naquele esquema: A fonte, no caso o sub A, se aproximando do observador, sub B, lança ondas na direção dele e esse as reflete, passando a ser considerado uma nova fonte de onda.
Show?
Bom, isso é o que eles pensam...
Mas tudo bem. Vamos fingir que também fomos enganados rs. Vamos chamar de a velocidade falsa de B. Então, resolvendo em duas etapas:
A fonte se aproximando de vai fazer com que sinta frequências de acordo com a fórmula:
Beleza! Agora, a nova fonte de ondas que passamos a considerar é o . Essa fonte se aproxima do observador com uma velocidade , a velocidade que vamos determinar, e emite ondas numa frequência . Então:
Ah, é claro, os engenheiros do submarino medem uma frequência .
Passo 5
Isolando :
Dividindo o segundo membro por no numerador e denominador:
Essa é a resposta. Mas se considerarmos que , podemos também responder que:
Ou seja, a velocidade é insignificante perto da grandeza da velocidade do som.
Resposta
a):
b):
c):
d):
Se considerarmos que podemos também responder que: