Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Comprimento de Onda de De Broglie

Ver Todos os Exercícios

Teoria

Opaa! E ai, bora aprender o que é o Comprimento de onda de De Broglie, com o RespondeAí?

Então pra começar, eu vou te contar uma historinha!

Lá por volta de 1707, Newton apresentou uma teoria sobre a dualidade onda-partícula da luz. Ele dizia que, apesar da luz observada por nós tem comportamento de partícula, no aspecto microscópico, ou seja se a gente ampliar muito vai conseguir observar que ela também realiza fenômeno ondulatório.

Comportamento ondulatório da luz.
Comportamento ondulatório da luz.

-Beleza, mas a gente não vai falar de De Broglie aqui?!

Calma, vamos sim! É que essa percepção do comportamento da luz proposto por Newton deu uma ideia para De Broglie! 💡💡💡

Com isso, Louis de Broglie sugeriu que a matéria também tivesse características de ondas e de partículas, e propôs relacionar um comprimento de onda  às partículas de matéria.

Assim, o comprimento de onda de De Broglie, também chamado de Onda de matéria é dado pela razão entre a constante de Plank e o momento linear da partícula .

Essas equação é valida para qualquer tipo de matéria, ou seja VOCÊ TAMBÉM TEM UM COMPRIMENTO DE ONDA! 😱😱😱

Mas calma lá, porque no caso de corpos macroscópicos, os comprimentos de onda são tão pequenos que é impossível observar propriedades ondulatórias perceptíveis.

Elétrons de Baixa Energia

A situação é diferente para elétrons de baixa energia.

Vamos ver um exemplo, imagina um elétron que possua energia cinética qual será o seu comprimento de onda?

O momento linear clássico para uma partícula é dado por:

E vamos precisar relacionar ele com a energia cinética que é dada por:

Multiplicando os dois lados por .

Daí temos:

Logo, o seu comprimento de onda será dado por:

Vamos calcular o comprimento de onda associado ao elétron. Multiplicando o numerador e o denominador por  a gente pode encontrar uma forma de encontrar o comprimento de onda em nanômetros  pra energia cinética em elétron-Volt .

Onde  e   e enfim temos a fórmula que nos dá o resultado já em nanômetros para um elétron com energia em .

Lembrando que quando for necessário utilizar a energia em  ou converter pra  a relação é:

Então substituindo nossa energia cinética temos:

Obs: Cuidado para não confundir a unidade de medida elétron-Volt com o produto da carga do elétron pela diferença de potencial . É importante ficar ligado no contexto.

Para o elétron, o seu comprimento de onda associado é muito próximo do seu “tamanho” e, por isso, o seu comportamento ondulatório é muito acentuado!

Por isso é possível observar o comportamento ondulatório do elétron, sendo ele sujeito aos fenômenos de interferência (quando duas ondas interferem uma na outra) e difração.

O comprimento de onda perceptível está na ordem até , por isso se a gente pegar um corpo macroscópico não vamos conseguir perceber, saca só esse exemplo.

Exemplo:

Uma bola de tênis possui massa , é lançada numa velocidade de . Sabendo que a constante de planck é  avaliar se há comportamento ondulatório pra bola.

Aqui vamos usar o comprimento de onda de De Broglie e avaliar se tem um movimento ondulatório perceptível.

Substituindo os valores:

E voltando no , podemos substituir e encontrar:

Então veja, é muito menor podemos considerar que é quase zero pra efeito de comprimento de onda. Então mostramos que corpos macroscópicos não possuem características ondulatórias perceptíveis.

Dualidade onda-partícula

Pra encerrar, vamos resumir as ideias que a gente conheceu nesse tópico!

A luz, que é uma onda, exibe propriedades corpusculares também quando interage com a matéria, como no efeito fotoelétrico e no espalhamento Compton onde ela transfere momento linear.

Os elétrons, que são partículas, exibem propriedades ondulatórias, como interferência e difração.

“Tudo se propaga como se fosse uma onda e troca energia como se fosse uma partícula.”

Confira aqui em baixo nosso conteúdo em vídeo! 👇🏻

Beleza! Vamos praticar?

Elétrons de Baixa Energia

Exemplo:

Dualidade onda-partícula

Exercícios Resolvidos

Exercício Resolvido #1

Halliday, Resnick, Jearl Walker, Fundamentos de física, volume 4: Óptica e Física Moderna, 8ª ed. Rio de Janeiro: LTC, 2009, pp 210-42.

Calcule o comprimento de onda de de Broglie:

  1. De um elétron de 1,00   K e V .
  2. De um fóton de 1,00   K e V .
  3. De um nêutron de 1,00   K e V .

Dados:

Massa do elétron m e = 9,109 ∙ 10 - 31   K g

Massa do nêutron m n = 1,675 ∙ 10 - 27   K g

Passo 1

O comprimento de onda de de Broglie de uma partícula é:

λ = h p

Onde p é o momento linear da partícula.

Passo 2

Letra a)

Considerando que toda a energia do elétron é cinética, temos:

K = 1,00   K e V

Onde K é a energia cinética do elétron. Além disso:

p 2 = 2 m K

E ficamos com:

λ = h 2 m K

Temos:

  • h = 6,626 ∙ 10 - 34   J ∙ s
  • m e = 9,109 ∙ 10 - 31   K g
  • K = 1,00   K e V = 1,602 ∙ 10 - 16   J

λ = 6,626 ∙ 10 - 34   2 ∙ 9,109 ∙ 10 - 31 ∙ 1,602 ∙ 10 - 16 ≅ 3,879 ∙ 10 - 11   m = 0,03879   n m

Passo 3

Letra b)

Para o fóton podemos usar que

p = E c

O que nos dá:

λ = h c E

  • h = 6,626 ∙ 10 - 34   J ∙ s
  • c = 2,998 ∙ 10 8   m / s
  • E = 1,00   K e V = 1,602 ∙ 10 - 16   J

λ = 6,626 ∙ 10 - 34 ∙ 2,998 ∙ 10 8 1,602 ∙ 10 - 16 = 1,24 ∙ 10 - 9   m =   1,24   n m

Passo 4

Letra c)

Assim como no item a :

λ = h 2 m K

Porém dessa vez usamos a massa do nêutron.

m n = 1,675 ∙ 10 - 27   K g

λ = 6,626 ∙ 10 - 34   2 ∙ 1,675 ∙ 10 - 27 ∙ 1,602 ∙ 10 - 16 ≅ 9,04 ∙ 10 - 13   m = 0,0009044   n m

Resposta

Letra a)

λ = 0,03879   n m

Letra b)

λ =   1,24   n m

Letra c)

λ = 0,0009044   n m

Exercício Resolvido #2

Young e Freedman, Física IV Ótica e Física Moderna, 12ª ed, São Paulo: Addison Wesley, 2009, pp 237-39.11.

Calcule o comprimento de onda de De Broglie de uma bala de 5   g que se desloca com velocidade igual a 340   m / s .

A bala exibirá propriedades semelhantes a ondas?

Passo 1

O comprimento de onda é dado por:

λ = h c 2 m c 2 K

Passo 2

K = 1 2 m v 2

Onde:

m = 5   g = 5 × 10 - 3   k g ;

v = 340   m / s ;

Logo:

K = 0,5 × 5 × 10 - 3 × 340 2 = 289   J

Passo 3

λ = h c 2 m c 2 K

Onde:

K = 289   J ;

h = 6,626 × 10 - 34   J   s ;

m = 5   g = 5 × 10 - 3   k g ;

c = 3 × 10 8   m / s ;

Logo:

λ = 6,626 × 10 - 34 × 3 × 10 8 2 × 5 × 10 - 3 × 9 × 10 16 × 289

λ = 3,90 × 10 - 34   m

Resposta

3,90 × 10 - 34   m ;

Não, pois o comprimento de onda é muito pequeno, tornando impossível observar propriedades ondulatórias perceptíveis.

Exercício Resolvido #3

UFRJ, Física 4, Prova 2, 2014.1.

Para que um próton, um elétron, e um fóton tenham todos o mesmo comprimento de onda de de Broglie associado, eles precisam ter:

a ) O mesmo momento angular.

b ) O mesmo momento linear.

c ) A mesma velocidade.

d ) A mesma energia.

e ) Um fóton, por ter massa de repouso nula, não pode ter o mesmo comprimento de onda de de Broglie associado que uma partícula cuja massa de repouso não seja nula.

f ) Nenhuma das anteriores

Passo 1

O comprimento de onda de de Broglie é dado por:

λ = h p

Assim, como h é uma constante, o comprimento de onda de de Broglie depende somente do momento linear.

Portanto, para que tanto o próton, quanto o elétron e o fóton tenham o mesmo comprimento de onda de de Broglie, é necessário todos tenham o mesmo momento linear.

A resposta certa é a letra b .

Resposta

b ) O mesmo momento linear.

Exercício Resolvido #4

Halliday, Resnick, Jearl Walker, Fundamentos de física, volume 4: Óptica e Física Moderna, 8ª ed. Rio de Janeiro: LTC, 2009, pp 210-51, modificado.

Uma partícula não-relativística está se movendo três vezes mais depressa que um elétron.

A razão entre o comprimento de onda de de Broglie da partícula e o comprimento de onda de de Broglie do elétron é 1,813 ∙ 10 - 4 .

Identifique a partícula, calculando sua massa.

Dado:

Massa do elétron m e = 9,109 ∙ 10 - 31   K g

Passo 1

Faaala, galera!! Vamos resolver essa questãozinha sobre um assunto bem cotidiano não é mesmo!? rs

A gente tem essa partícula doida aí viajando rapidão e precisamos calcular sua massa. O problema fala bastante do elétron também, então a gente provavelmente vai ter que comparar as duas partículas para descobrir a massa da nossa partícula doida.

Pessoal, vamos dar uma olhada no comprimento de onda de De Broglie de uma partícula, que é dado por:

λ = h p = h m v

Assim, a gente pode definir uma razão entre o comprimento de onda da partícula e o do elétron. Que vai ser:

λ λ e = h m v ∙ m e v e h

λ λ e = m e v e m v

Viu como apareceu uma razão entre as grandezas envolvendo o elétron e a nossa partícula? Na real para resolver esse problema é só substituir os valores fornecidos nessa equação, mas vamos fazer isso devagarinho =D

Passo 2

O enunciado nos diz que a velocidade da partícula é três vezes a do elétron.

v = 3 v e

E nos diz também a massa do elétron:

m e = 9,109 ∙ 10 - 31   K g

Assim como a relação entre os comprimentos de onda:

λ λ e = 1,813 ∙ 10 - 4

Dessa forma podemos substituir na nossa equação do passo 1:

λ λ e = m e v e m v

Substituindo:

1,813.10 - 4 = 9,109.10 - 31 ( v e ) m ( 3 v e )

Aí podemos cortar v e e reorganizar:

m = 9,109 ∙ 10 - 31 3 ∙ 1,813 ∙ 10 - 4 = 1,675 ∙ 10 - 27   K g

Na verdade, essa é a massa de um nêutron!

Resposta

m = 1,675 ∙ 10 - 27   K g

Exercício Resolvido #5

Halliday, Resnick, Jearl Walker, Fundamentos de física, volume 4: Óptica e Física Moderna, 8ª ed. Rio de Janeiro: LTC, 2009, pp 207-12.

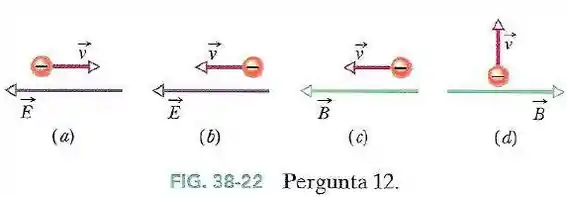
A Fig.38-22 mostra um elétron que se move:

  1. No sentido oposto ao de um campo elétrico.
  2. No mesmo sentido que um campo elétrico.
  3. No mesmo sentido que um campo magnético.
  4. Perpendicularmente a um campo magnético.

Determine, para cada uma das situações, se o comprimento de onda de de Broglie aumenta com o tempo, diminui com o tempo ou permanece constante.

Passo 1

O comprimento de onda de de Broglie do elétron é dado por:

λ = h p = h m v

Quando o elétron for não relativístico.

Essa fórmula nos diz que, quanto maior a velocidade do elétron, menor seu comprimento de de Broglie.

Passo 2

Na letra a , a carga negativa tem inicialmente uma velocidade com sentido oposto ao campo elétrico.

Mas pela carga ser negativa irá atuar sobre ela uma força elétrica que aumenta sua velocidade.

F e l → = - q E →

Logo seu comprimento de onda de de Broglie diminui.

Já na letra b a carga negativa tem uma velocidade no mesmo sentido do campo elétrico, mas vai ter uma força atuando no sentido oposto. Isso freia a partícula, diminuindo sua velocidade.

Com a sua velocidade diminuindo seu comprimento de onda de de Broglie aumenta.

Passo 3

A força que atua numa carga em movimento devido a uma força elétrica é:

F B → = q v → × B →

Em módulo:

F B = q v B sen ⁡ θ

Onde θ é o ângulo entre v → e B → .

Assim, quando a partícula se movimento paralelamente ao campo magnético temos θ = 0 e não atua nenhuma força nela, mantendo sua velocidade constante.

Por isso seu comprimento de onda de de Broglie é constante.

Quando o movimento da partícula é perpendicular ao campo magnético, ela sofre uma força magnética perpendicular ao seu movimento.

Pela força ser perpendicular ao movimento ela não altera o módulo da velocidade, apenas sua direção. (Colocado de outra forma: Forças perpendiculares não realizam trabalho).

Por isso, novamente, o comprimento de onda de de Broglie do elétron é constante.

Resposta

Caso a) Comprimento de onda de de Broglie diminui.

Caso b) Comprimento de onda de de Broglie aumenta.

Caso c) O comprimento de onda de de Broglie não muda.

Caso d) O comprimento de onda de de Broglie não muda.

Exercício Resolvido #6

Halliday, Resnick, Jearl Walker, Fundamentos de física, volume 4: Óptica e Física Moderna, 8ª ed. Rio de Janeiro: LTC, 2009, pp 210-43, modificado.

No tubo de imagem de um velho aparelho de televisão os elétrons são acelerados por uma diferença de potencial de 25,0   k V .

Qual é o comprimento de onda de de Broglie desses elétrons?

(Não é necessário levar em conta efeitos relativísticos)

Dado:

Massa do elétron m e = 9,109 ∙ 10 - 31   K g

Passo 1

O comprimento de onda de de Broglie do elétron (não relativístico) é:

λ = h p = h 2 m K

Onde K é a energia cinética do elétron, e p 2 = 2 m K .

Quando o elétron é acelerado por uma diferença de potencial, ele adquire uma energia cinética igual a energia elétrica que ele recebe.

K = e ∙ V

Temos que e = 1,602 ∙ 10 - 19 C é a carga do elétron (carga elementar) e V = 25,0   k V é a diferença de potencial (de acordo com o enunciado).

Assim:

λ = h 2 m e V

Passo 2

Vamos listar o valor de cada coisa e substituir na fórmula:

  • h = 6,626 ∙ 10 - 34   J ∙ s
  • m e = 9,109 ∙ 10 - 31   K g
  • e = 1,602 ∙ 10 - 19 C
  • V = 25,0   k V = 25 ∙ 10 3   V

λ = h 2 m e e V = 6,626 ∙ 10 - 34 2 ∙ 9,109 ∙ 10 - 31 ∙ 1,602 ∙ 10 - 19 ∙ 25 ∙ 10 3 ≅ 6,626 ∙ 10 - 34 7,296309 ∙ 10 - 45

λ ≅ 6,626 ∙ 10 - 34 0,854184 ∙ 10 - 22 ≅ 7,757 ∙ 10 - 12   m = 7,757   p m

Resposta

λ ≅ 7,757   p m

Exercício Resolvido #7

Halliday, Resnick, Jearl Walker, Fundamentos de física, volume 4: Óptica e Física Moderna, 8ª ed. Rio de Janeiro: LTC, 2009, pp 210-47, modificado.

Íons monovalentes de sódio são acelerados por uma diferença de potencial de 300   V .

  1. Qual é o momento final dos íons?
  2. Qual é o comprimento de de Broglie correspondente?

Dado:

Massa molar do sódio m N a = 22,9898   g / m o l

Constante de Avogrado 1   m o l = 6,022 ∙ 10 23   u n i d a d e s

Passo 1

Letra a)

Os íons adquirem uma energia cinética igual a energia elétrica impressa neles.

K = q ∙ V

Onde V é a carga do íon. Como o íon é monovalente, falta um elétron a ele, e sua carga fica igual a carga elementar.

q = e = 1,602 ∙ 10 - 19   C

E pelo enunciado V = 300   V .

K = e ∙ V = 1,602 ∙ 10 - 19 ∙ 300 = 4,806 ∙ 10 - 17   J

Passo 2

O momento final dos íons se relaciona com a energia cinética obtida por eles.

p = 2 m K

Sendo que m é a massa de um único átomo de sódio.

Um mol de átomos de sódio tem uma massa de m N a = 22,9898   g / m o l . Fazendo uma regra de três, podemos achar a massa de um único átomo.

m = 22,9898 6,022 ∙ 10 23 ≅ 3,818 ∙ 10 - 23   g = 3,818 ∙ 10 - 26 K g

Substituindo tudo:

p = 2 ∙ 3,818 ∙ 10 - 26 ∙ 4,806 ∙ 10 - 17 ≅ 1,9156 ∙ 10 - 21   K g ∙ m / s

Passo 3

Letra b)

O comprimento de onda de de Broglie é

λ = h p

Temos:

  • h = 6,626 ∙ 10 - 34   J ∙ s
  • p = 1,9156 ∙ 10 - 21   K g ∙ m / s

λ = 6,626 ∙ 10 - 34 1,9156 ∙ 10 - 21 ≅ 3,459 ∙ 10 - 13   m = 0,3459   p m

Resposta

Letra a)

p ≅ 1,9156 ∙ 10 - 21   K g ∙ m / s

Letra b)

λ ≅ 3,459 ∙ 10 - 13   m = 0,3459   p m

Exercícios de Livros Relacionados

Um elétron está se movendo a 2,5×10 5m/s . Encontre o comprimento de onda de elétron de Broglie.
Exercício de Livro
Um próton e um elétron têm energias cinéticas iguais. Segue-se que o comprimento de onda do próton é (a) maior que o comprimento de onda do elétron, (b) igual ao comprimento de onda do elétron, (c) me
Se o comprimento de onda de um elétron é igual ao comprimento de onda de um próton, (a) a velocidade do próton é maior que a velocidade do elétron, (b) as velocidades do próton e do elétron são iguais
Um elétron, um próton e uma partícula alfa possuem energia cinéticade 150 keV. Encontre (a) as magnitudes de seus momentos e (b) seus comprimentos de onda de De Broglie.