Equação de Schrödinger
Produzido por Bruno SoaresTeoria
A função de onda de uma partícula
“Deixai toda a normalidade, ó vós que entrais”
Vamos falar de Mecânica Quântica.
Partículas se comportam tanto como onda quanto como partícula, certo?
Bem, quando você não está olhando, elas se comportam exatamente como uma onda viajando por aí. Essa onda é representada por uma função de onda . É ela que vai descrever tudo sobre o seu sistema.
Interpretando a função de onda
Agora que as partículas se movem como ondas, é complicado dizer “onde” elas estão, porque as ondas são “espalhadas” por natureza.
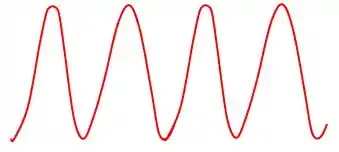
Então o que pode significar essa onda que representa uma partícula?
Bem, vamos imaginar que de alguma forma eu prendi um elétron e vou medir a sua posição mesmo assim. Onde eu encontrá-lo, eu vou marcar um pontinho preto.
Eu meço uma, duas, três... mil quatrocentos e sessenta e oito, ...muitas vezes. Algo surpreendente vai acontecer: minha função de onda vai aparecer nos meus pontinhos!

Os lugares onde eu encontrei o elétron várias vezes vão estar bem concentrados com pontinhos pretos, enquanto os lugares onde eu quase nunca encontrei vão estar quase sem pontinhos.
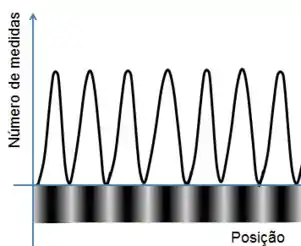
Isso nos dá uma ideia de o que pode significar a função de onda: ela tem a ver com a probabilidade de eu encontrar o elétron.
Densidade de probabilidade
Imagina que o elétron se move de um lado pro outro apenas ao longo do eixo . A probabilidade de o encontrarmos entre duas posições e vai ser:
O quadrado da função de onda é a chamada densidade de probabilidade de se encontrar a partícula em algum lugar do espaço. Numa região bem pequenininha onde é praticamente constante, tem-se:
“Densidade” é quando massa divide por volume né? Então, densidade de probabilidade é como se fosse “probabilidade dividida por volume”! Pra quem gosta de linguajar mais formal, é a função de distribuição de probabilidade do elétron.
Isso nos dá uma idéia da dimensão de quando a função de onda é unidimensional.
Pois “probabilidade” não tem unidade. Em geral, e no lugar de teríamos . Assim, a sua unidade seria:
Esse é o significado da função de onda. Ok, na verdade do quadrado dela. Mas a função de onda sozinha não tem muito significado físico: é o seu quadrado que nós vamos buscar pra ficar monstro!
Normalização
Imagine agora que você olha em todo o eixo , de a . Em algum lugar o elétron TEM que estar, a não ser que tenhamos sido roubados! Então a probabilidade de ela estar em toda a reta é de , ou seja, .
Isso é chamado condição de normalização da função de onda, que diz que:
Neste caso dizemos que a função de onda está normalizada.
Outra coisa importante sobre a função de onda é que ela deve ser contínua. Isso significa que o valor dela não pode “pular” de repente de um valor pra outro.
Por fim, um último comentário.
A função de onda pode variar ao longo do espaço, mas ela também pode ir mudando com o tempo. Isso significa que ela depende de e de (tempo).
Porém muitas vezes podemos separar a dependência do tempo e do espaço, e vai ser na parte do espaço que estaremos interessados, pois iremos observar problemas onde os estados são estacionários, ou seja, a densidade de probabilidade não muda com o tempo.
Por isso na condição de normalização estamos integrando .
Lá na Física Clássica...
Uma das coisas mais essenciais de toda a física clássica são as leis de Newton.
Uma delas em específico nos diz tudo sobre o movimento de blocos de madeira, bolas de gude, molas com pesos, etc... É a famosa .
Se soubermos a força que atua no bloquinho, sabemos sua aceleração, e sabemos como o bloquinho está se movimentando.
Aqui na Mecânica Quântica...
Na Mecânica Quântica, nós vamos ter uma “lei” semelhante. Neste caso, nós temos a Equação de Schrödinger, que dita como a função de onda vai variar com a posição e o tempo.
Onde é a massa da partícula, é a constante de Planck reduzida e é a energia potencial da partícula em função de sua posição.
O que vai nos importar são os chamados casos estacionários, onde a densidade de probabilidade não varia com o tempo.
Nestes casos nós podemos separar a função de onda em uma parte que depende apenas de , , e uma parte que depende apenas do tempo .
Se substituirmos na equação, obteremos duas novas equações:
Onde é a energia do sistema, que diz respeito a parte temporal. A solução dessa equação vai ser:
Pra parte que depende do espaço, vamos ter a equação de Schrödinger independente do tempo:
E essa é a parte que vai nos importar, pois ela vai definir a função de onda do sistema.
Essa equação nos dá a energia total da nossa partícula. O primeiro termo representa a energia cinética, o segundo a energia potencial e o último, a energia total.
Energia Cinética
Energia Potencial
Energia Total
A função de onda total dependente do tempo será:
Princípio da Incerteza de Heinsenberg
A mecânica quântica tem uma incerteza inerente:
É impossível medir com precisão tanto a posição quanto o momento linear de uma partícula.
Se um for muito preciso, o outro é pouco preciso, e vice-versa.
Quando fizermos a medição da posição e do momento linear várias vezes, teremos uma incerteza na posição e uma incerteza no momento linear ao longo do eixo que serão os desvios padrões das nossas medidas.
Neste caso, o Princípio da Incerteza de Heisenberg diz que:
Onde é às vezes chamada de constante de Planck reduzida e é a constante de Planck.
OBS: Alguns livros adotam que , mas aqui vamos usar , beleza?
Se a onda é bem concentrada, é baixo, e podemos dizer bem onde ela está. Porém, isso faz com que tenha que ser alto, e é difícil dizer a velocidade com que ela está andando.
Contudo, se pudermos dizer seu momento linear com bastante precisão, a incerteza é baixa, e por isso vai ser alta, sendo difícil dizer “aonde” a onda está.
Se a partícula se mover numa direção qualquer no espaço (em três dimensões), então na verdade eu vou ter uma relação de incerteza em cada eixo:
Onde a incerteza da posição em cada eixo se relaciona com a incerteza da componente do momento linear naquele eixo.
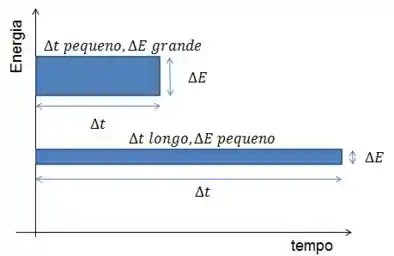
Outra relação que, embora seja parecida, não é bem a mesma coisa é o Princípio da Incerteza da energia e do tempo.
Neste caso, a relação é entre a incerteza na nossa medida de energia e o tempo que a partícula continua tendo aquela mesma energia.
Onde é a incerteza na energia, mas NÃO é a incerteza no tempo, e sim o tempo médio que a partícula vai continuar com a mesma energia!
Isso significa que, se for o intervalo para a medição de energia de um sistema, a medição terá uma incerteza .
Densidade de probabilidade
Normalização
Lá na Física Clássica...
Aqui na Mecânica Quântica...
Princípio da Incerteza de Heinsenberg
Exercícios Resolvidos
Exercício Resolvido #1
Halliday, Resnick, Jearl Walker, Fundamentos de física, volume 4: Óptica e Física Moderna, 8ª ed. Rio de Janeiro: LTC, 2009, pp 211-63.
A indeterminação da posição de um elétron situado sobre o eixo é , ou seja, um valor aproximadamente igual ao raio de um átomo de hidrogênio.
Qual é a menor indeterminação possível da componente do momento do elétron?
Passo 1
Para resolver esse problema a gente precisa do princípio da incerteza de Heisenberg que nos diz:
Onde é a incerteza do momento linear do elétron e é a incerteza na posição do elétron. Perceba que o problema fornece e pede , além disso é uma constante. Sendo assim basta substituir =D
Passo 2
Como , teremos:
A constante vale . Substituindo:
O menor valor possível então vai ser:
Resposta
Exercício Resolvido #2
Young e Freedman, Física IV Ótica e Física Moderna, 12ª ed, São Paulo: Addison Wesley, 2009, pp 237-39.21.
Um cientista descobriu um método para isolar partículas individuais.
Ele alega que seu método permite a medida simultânea da posição da partícula ao longo de um eixo com um desvio-padrão de e a medida do componente do momento linear ao longo do mesmo eixo com um desvio-padrão de .
Use o princípio da incerteza de Heisenberg para verificar a validade dessa alegação.
Passo 1
O problema nos dá o desvio-padrão da posição e o desvio-padrão do momento linear .
Como estamos trabalhando com os desvios-padrões, de acordo com o princípio da incerteza, os dois estão relacionados por:
Onde .
Passo 2
Onde:
;
;
;
Logo:
Como esse resultado é matematicamente errado, temos uma inconsistência. Portanto, a alegação não é válida.
Resposta
A alegação não é válida.
Exercício Resolvido #3
Young e Freedman, Física IV Ótica e Física Moderna, 12ª ed, São Paulo: Addison Wesley, 2009, pp 237-39.23.
Um átomo em um estado metaestável possui vida média igual a .
Qual é a incerteza na energia do estado metaestável?
Passo 1
O tempo e a energia também se correlacionam por um princípio próprio de incerteza.
Podemos associar a incerteza da energia com o tempo que ele leva no estado metaestável , o que nos dá:
Passo 2
Usaremos a igualdade para calcular a incerteza da energia, assim:
Onde:
;
;
Logo:
Como
Se consideramos que o produto é aproximadamente da ordem de , então:
Resposta
Exercício Resolvido #4
Halliday, Resnick, Jearl Walker, Fundamentos de física, volume 4: Óptica e Física Moderna, 8ª ed. Rio de Janeiro: LTC, 2009, pp 211-57, modificado.
Mostre que a Eq.38-17 é uma solução da Eq.38-16 substituindo e sua derivada segunda na Eq.38-16 e observando que o resultado é uma identidade.
Dados:
Equação 38-16 (Equação de Schrödinger, partícula livre):
Equação 38-17:
Passo 1
Vamos derivar a função :
Agora, como , vamos rearranjar a segunda derivada:
Note que:
Ou seja, já provamos direto que:
Resposta
Ei, a resposta está no passo a passo :)
Exercício Resolvido #5
Halliday, Resnick, Jearl Walker, Fundamentos de física, volume 4: Óptica e Física Moderna, 8ª ed. Rio de Janeiro: LTC, 2009, pp 244-63, modificado.
- Mostre que os termos da equação de Schrödinger (Eq.39-18) têm a mesma dimensão.
- Qual é a unidade desses termos no SI?
Dado:
Equação 39-18
Onde é a função de onda, é a massa de uma partícula, é a constante de Planck, é a energia mecânica total e é a energia potencial da partícula.
Passo 1
Letra a)
Vamos começar pelo primeiro termo.
Esse termo tem a unidade da função de onda divido pela unidade da variável ao quadrado, que é . Seja a unidade da função de onda. A unidade desse termo será:
Passo 2
Agora vamos para o segundo termo.
A sua unidade vai ser a unidade da função de onda multiplicada pela unidade de .
A unidade de massa é . A unidade da constante de Planck é . Logo:
A unidade de energia é Joule( ).A unidade do termo entre colchetes então é Joule. Juntando tudo:
Agora, vamos abrir a unidade de energia.
Substituindo:
A unidade do segundo termo vai ser:
Que é igual a unidade do primeiro termo.
Passo 3
Letra b)
Podemos usar o resultado do item anterior para achar a unidade dos dois termos no SI.
Como a função de onda ao quadrado é a densidade de probabilidade de se encontrar a partícula entre dois pontos do eixo , a unidade dele é:
A unidade da função de onda então vai ser a raiz quadrada disso:
A unidade dos termos será:
Resposta
Letra a)
Ambos os termos tem unidade de .
Letra b)
Exercício Resolvido #6
Halliday, Resnick, Jearl Walker, Fundamentos de física, volume 4: Óptica e Física Moderna, 8ª ed. Rio de Janeiro: LTC, 2009, pp 211-61, modificado.
A função da Eq.38-19 descreve uma partícula livre para a qual supusemos que na equação de Schrödinger (Eq.38-15).
Suponha que , onde é uma constante.
Mostre que a Eq.38-19 continua a ser uma solução da equação de Schrödinger, mas o valor do número de onda angular da partícula passa a ser dado por:
Dadas:
Equação 38-19
Equação 38-15 (Equação de Schrödinger, movimento unidimensional)
Passo 1
Vamos calcular a derivada segunda da função .
Mostramos nesse passo que:
Passo 2
Do passo anterior:
Porém, queremos reaver a equação de Schrödinger
Mas do enunciado, temos que é constante. Substituindo:
Para as duas equações serem a mesma, precisamos ter que:
Tirando a raiz quadrada:
Que é a expressão que desejamos.
Passo 3
Por fim, vamos apenas reconfirmar o que fizemos. Temos:
Resposta
Ei, a resposta está no passo a passo :)
Exercício Resolvido #7
Young e Freedman, Física IV Ótica e Física Moderna, 12ª ed, São Paulo: Addison Wesley, 2009, pp 238-39.31.
Considere uma partícula deslocando-se em uma dimensão, que chamaremos de eixo .
- O que significa para a função de onda dessa partícula ser normalizada?
- A função de onda , onda é um número real positivo, é normalizada? Essa função poderia ser válida?
- Se a partícula descrita pela função de onda , onde e são números reais positivos, estiver confinada ao intervalo , determine (inclusive suas unidades) de modo que a função de onda seja normalizada.
Passo 1
a) O que significa para a função de onda dessa partícula ser normalizada?
Para que a função de onda seja normalizada, ela deve obedecer à condição de normalização, dada por:
Portanto, a integral do quadrado da função de onda deve ser igual a um.
Passo 2
b) A função de onda , onde é um número real positivo, é normalizada? Essa função poderia ser válida?
Para que a função de onda seja normalizada, ela deve obedecer à condição de normalização, dada por:
Onde:
;
Logo:
A função não é normalizada. A função não é válida.
Passo 3
c) Se a partícula descrita pela função de onda , onde e são números reais positivos, estiver confinada ao intervalo , determine (inclusive suas unidades) de modo que a função de onda seja normalizada.
Para que a função de onda seja normalizada, ela deve obedecer à condição de normalização, dada por:
Neste caso:
Como , a condição de normalização será dada por:
Passo 4
De acordo com a condição de normalização, a integral
deve ser igual a um valor adimensional. Como representa a densidade de probabilidade, deve possuir unidade de medida de forma que o produto de por uma unidade de comprimento seja adimensional.
Assim:
Logo:
Resposta
a)
A integral da função de densidade de probabilidade entre limites infinitos deve ser igual a um.
b)
Não. Não. Não é uma função de onda válida.
c)
Exercício Resolvido #8
UFRJ, Física 4, Prova 2, 2012.1.
O Princípio da Incerteza de Heisenberg afirma que:
- Apenas o momento e a velocidade podem ser medidos com precisão ilimitada.
- A trajetória de uma partícula pode ser definida com precisão ilimitada usando a mecânica quântica.
- Nada é menor que a constante de Planck
- Momento e a posição de uma partícula não podem ser medidos simultaneamente com precisão ilimitada.
- Momento ou a velocidade, mas não ambos, podem ser medidos com precisão ilimitada.
- Nenhuma das afirmações anteriores está correta.
Passo 1
Vamos analisando as opções uma a uma.
a) Apenas o momento e a velocidade podem ser medidos com precisão ilimitada.
Isso não é verdade, o princípio da incerteza propõe uma margem de erro para medições da posição, energia, momento e tempo.
Passo 2
b) A trajetória de uma partícula pode ser definida com precisão ilimitada usando a mecânica quântica.
Não é verdade, a precisão da posição está relacionada com a precisão do momento através da relação.
E a trajetória de uma partícula é definida pela sua posição e momento.
Passo 3
c) Nada é menor que a constante de Planck
Não é verdade, o produto das incertezas da posição com a do momento e da energia com a do tempo deve ser sempre menores ou iguais à .
Passo 4
d) Momento e a posição de uma partícula não podem ser medidos simultaneamente com precisão ilimitada.
Está correto, bem como prevê o princípio da incerteza, que serve pra dar um parâmetro para a margem de erro.
Passo 5
e) Momento ou a velocidade, mas não ambos, podem ser medidos com precisão ilimitada.
Não é verdade, não há sequer menção à velocidade no princípio da incerteza.
Passo 6
f) Nenhuma das afirmações anteriores está correta.
Não é verdade. A letra (d) está correta.
Resposta
d) Momento e a posição de uma partícula não podem ser medidos simultaneamente com precisão ilimitada.
Exercício Resolvido #9
Young e Freedman, Física IV Ótica e Física Moderna, 12ª ed, São Paulo: Addison Wesley, 2009, pp 238-39.35.
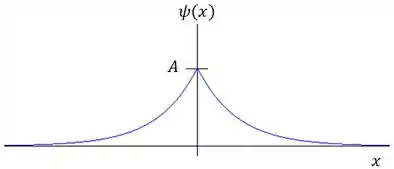
Uma partícula deslocando-se em uma dimensão (o eixo ) é descrita pela função de onda
Onde , , e o sentido positivo do eixo aponta para a direita.
- Determine de modo que a função de onda seja normalizada.
- Faça o gráfico da função de onda.
- Calcule a probabilidade de se encontrar essa partícula em cada uma das seguintes regiões.
- Até da origem
- Do lado esquerdo da origem (você pode adivinhar a resposta olhando para o gráfico da função de onda?).
- Entre e .
Passo 1
a) Determine de modo que a função de onda seja normalizada.
Para que a função de onda seja normalizada, ela deve obedecer à condição de normalização, dada por:
Passo 2
Onde:
;
Logo:
Passo 3
b) Faça o gráfico da função de onda.
A função de onda vai ser algo do tipo:
Passo 4
c) Calcule a probabilidade de se encontrar essa partícula em cada uma das seguintes regiões.
A probabilidade de se encontrar um elétron entre os pontos e , por sua vez, é dada por:
Passo 5
- Até da origem:
Como o problema fala de da origem, vamos calcular a probabilidade de se encontrar uma partícula entre e .
Para , e para , . Logo:
Onde:
;
;
Logo:
Passo 6
Do lado esquerdo da origem (você pode adivinhar a resposta olhando para o gráfico da função de onda?):
Do lado esquerdo da origem representa todos os valores negativos de e, de acordo com o gráfico, exatamente a metade do gráfico da função de onda .
Logo, a probabilidade de se encontrar uma partícula nessa região é .
Passo 7
Caso não dê pra identificar isso visualmente, podemos calcular a probabilidade com variando de até .
Para , . Logo:
Onde:
;
;
Logo:
Passo 8
Entre e .
Como estamos calculando a probabilidade em um intervalo onde , . Logo:
Onde:
;
;
Logo:
Resposta
a)
b)
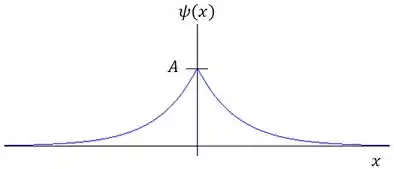
c)
(i):
(ii):
(iii):