Átomo de Bohr
Teoria
Introdução
Você que já chegou até aqui deve ter ouvido falar dos fótons, mas sabe me dizer como relacionamos os fótons e os elétrons?
Bohr desenvolveu um modelo atômico e escreveu alguns postulados, que nos ajudam a relacionar fótons e elétrons.
Ao longo dessa teoria vamos dar uma olhada em cada postulado, compreender as relações importantes entre os fótons e elétrons e também entender como a quântica trata do modelo atômico de Bohr.
Postulados de Bohr
Primeiro postulado de Bohr:
“O elétron do átomo de hidrogênio só pode se mover em certas órbitas, não-irradiantes, circulares, chamadas de estados estacionários. ”
Ele diz que tem que ser “não-irradiantes” porque, se o elétron irradiasse ondas eletromagnéticas, ele iria perdendo energia e iria saindo da órbita em uma espiral em direção ao núcleo.
E pelo modelo de Bohr do átomo a gente vê que as órbitas respeitam essa condição circular e estacionária.
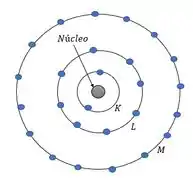
O átomo irradia somente quando o elétron faz uma transição de um estado estacionário para outro.
Segundo postulado de Bohr:
O segundo postulado explica como calcular a frequência da radiação emitida pelo elétron quando ele faz o movimento de transitar entre duas órbitas, como na figura:
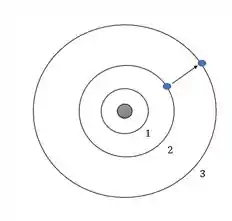
Aqui na quântica a gente vai ver o modelo de Bohr numerando as órbitas de até a partir do núcleo.
Nessa transição de camadas o elétron vai absorver ou emitir um fóton e a gente logo vai entender quando ocorre cada caso.
A frequência do fóton emitido pelo elétron na transição entre duas órbitas é relacionada à energia das órbitas por:
(Frequência do fóton emitido ou absorvido)
Onde é a constante de Planck, lembrando que . A energia corresponde à energia no estado inicial e corresponde à energia no estado final.
Terceiro postulado de Bohr:
As órbitas do elétron são tais que o momento angular do elétron em relação ao núcleo é um múltiplo inteiro de . Isso implica que o raio das órbitas é quantizado.
(Momento angular quantizado)
Onde .
O conceito importante desse postulado é semelhante ao do primeiro: órbitas estacionárias.
Raio das órbitas circulares
Agora vamos deduzir as características do átomo de Bohr, usando o que vimos nos postulados.
Vamos imaginar um elétron numa órbita circular de raio em torno de uma carga positiva , como o núcleo de hidrogênio ( é o número de prótons no núcleo de hidrogênio).
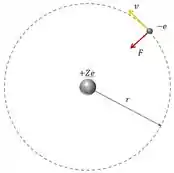
A força elétrica de atração entre as cargas que mantém o elétron na trajetória circular é igual a força centrípeta.
Da quantização do momento angular:
Igualando os dois podemos achar os raios das órbitas do elétron.
Onde é o menor raio possível para a órbita do elétron do hidrogênio. Lembrando que no hidrogênio, .
Raios das órbitas de Bohr
Se calcularmos os valores da equação é possível encontrarmos o valor
E em nanômetros temos:
Mas esse é um valor que costuma ser dado, então vamos guardar nossas energias pra compreender como resolver problemas envolvendo essa constante.
Reescrevendo a equação do raio das órbitas de Bohr para um valor em nanômetros, temos:
Energia das Órbitas
A energia total do elétron é igual à soma da energia potencial com a energia cinética.
A energia potencial é dada por:
A energia cinética é dada por:
Logo o que foi encontrado pra
Substituindo esse resultado na expressão da energia, temos:
Finalmente:
Podemos substituir pelos raios das órbitas, e teremos:
Ou:
Níveis de energia para o átomo de hidrogênio
Quando
Onde:
corresponde ao estado de energia mais baixa, também chamado de estado fundamental.
E se liga, nas provas não é comum aparecerem os dados para calculá-lo então guarde bem esse valor!
Para outros átomos com só um elétron com diferentes (chamados de átomos hidrogenóides)
Os exercícios mais comuns devem te pedir pra calcular a diferença de energia na transição dos estados, então pra fixar essa equação da energia vamos calcular pra essa situação da figura a diferença de energia:
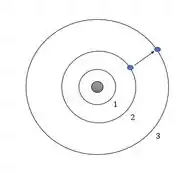
Aqui o elétron saiu da órbita de e foi para a órbita de , vamos usar a equação da energia para cada órbita:
A variação da energia nada mais é que a energia do fóton emitido ou absorvido no processo.
E o sinal é positivo pois para o elétron sair do estado 2 para o estado 3 ele precisa absorver energia, então o que aconteceu aí foi uma absorção
Se por acaso ele fizesse o movimento contrário, ou seja, quando ele diminui de órbita da 3 pra 2 ele emite um fóton perdendo energia. Dizemos que aí acontece uma emissão.
Fóton emitido na transição eletrônica
Se o elétron vai de uma órbita inicial para uma órbita final a energia do fóton associado é
Se quer dizer que tivemos um fóton absorvido e se tivemos um fóton emitido. Fica atento nisso!
O ter sinal positivo ou negativo faz sentido, mas no final da sua conta você tem que ter positiva, você pode usar o módulo do valor encontrado caso esteja trabalhando com uma emissão.
Isolando a frequência, temos:
Se usarmos que , temos a fórmula das séries do hidrogênio, outra parada é que passamos o sinal pra dentro do parêntese e aí temos que trocar a ordem das frações.
Onde é a constante de Rydberg dada por:
E se por acaso no nosso exemplo quiséssemos saber o comprimento de onda do fóton emitido? Era só a gente rearrumar a fórmula das séries do hidrogênio em função de
E como a gente já sabe que o elétron saiu da órbita de para é só substituirmos os valores:
Substituindo a constante temos:
E olha que interessante, esse comprimento de onda está na faixa dos comprimentos da luz vermelha .
É importante entender o desenvolvimento para entender o conceito do átomo de Bohr. Mas não se preocupe com as sopas de letrinhas nas constantes, foque em entender quem são as constantes e quando usá-las.
Resumo
Níveis de energia para o átomo de hidrogênio
Raios das órbitas de Bohr
Momento angular
Série do Hidrogênio
Raio das órbitas circulares
Energia das Órbitas
Fóton emitido na transição eletrônica
Resumo
Exercícios Resolvidos
Exercício Resolvido #1
Young e Freedman, Física IV Ótica e Física Moderna, 12ª ed, São Paulo: Addison Wesley, 2009, pp 212-38.23.
Um átomo de hidrogênio está em um estado com energia .
No modelo de Bohr, qual é o momento angular do elétron no átomo, em relação a um eixo que passa pelo núcleo?
Passo 1
De acordo com o modelo de Bohr, o momento angular do elétron é dado por:
Onde:
O problema nos dá que o átomo está em um estado de energia com .
O níveis de energia são dados por:
Passo 2
Para o átomo de hidrogênio, . Então podemos descobrir o valor de , através da expressão:
Onde:
;
(valor constante);
;
Logo:
Passo 3
Voltando para a expressão do momento angular:
Onde:
;
;
Logo:
Resposta
Exercício Resolvido #2
Young e Freedman, Física IV Ótica e Física Moderna, 12ª ed, São Paulo: Addison Wesley, 2009, pp 212-38.27.
- Usando o modelo de Bohr, calcule a velocidade do elétron no átomo de hidrogênio para os níveis e .
- Calcule o período orbital para cada um desses níveis.
- A vida média para o primeiro nível excitado do átomo de hidrogênio é . No modelo de Bohr, quantas voltas completas o elétron daria no nível antes de o elétron voltar para seu nível fundamental?
Passo 1
a) Usando o modelo de Bohr, calcule a velocidade do elétron no átomo de hidrogênio para os níveis e .
Podemos relacionar as velocidades e os níveis através do momento angular, dado por:
Os raios dos níveis são dados por:
Passo 2
Vamos encontrar os raios para e .
Onde:
(para o hidrogênio);
;
Logo:
Passo 3
Onde:
;
;
;
;
;
Logo:
Passo 4
b) Calcule o período orbital para cada um desses níveis.
Considerando a trajetória circular dos elétrons:
Onde:
;
;
;
;
;
;
Logo:
Passo 5
c) A vida média para o primeiro nível excitado do átomo de hidrogênio é . No modelo de Bohr, quantas voltas completas o elétron daria no nível antes de o elétron voltar para seu nível fundamental?
O período para o nível é .
Para saber o número de voltas que o elétron daria, basta calcular:
Resposta
a)
b)
c)
Exercício Resolvido #3
UFRJ, Física 4, Prova 2, 2012.1.
A condição de quantização de Bohr para as órbitas dos elétrons requer que:
- O momento angular do elétron em torno do núcleo do átomo de hidrogênio seja igual a
- No máximo um elétron ocupe um dado estado estacionário.
- Os elétrons espiralem em direção ao núcleo enquanto irradiam ondas eletromagnéticas.
- As energias possíveis para um elétron num átomo de hidrogênio sejam iguais a , onde é uma constante e um número inteiro.
- Nenhuma das afirmações anteriores está correta.
Passo 1
Vamos analisando opção por opção.
a) O momento angular do elétron em torno do núcleo do átomo de hidrogênio seja igual a .
De acordo com Bohr, o momento angular de um elétron em torno do núcleo do átomo é igual a .
Logo, a opção está correta.
Passo 2
b) No máximo um elétron ocupe um dado estado estacionário.
No modelo de Bohr para o átomo não há nenhuma restrição quanto ao número de elétrons em um mesmo estado estacionário.
Passo 3
c) Os elétrons espiralem em direção ao núcleo enquanto irradiam ondas eletromagnéticas.
Os elétrons não devem irradiar ondas eletromagnéticas, pois iriam percorrer uma trajetória em espiral e o átomo colapsaria.
A opção está incorreta.
Passo 4
d) As energias possíveis para um elétron num átomo de hidrogênio sejam iguais a , onde é uma constante e um número inteiro.
As energias possíveis para um elétron num átomo de hidrogênio são dadas por:
Logo, a opção está incorreta.
Passo 5
e) Nenhuma das afirmações anteriores está correta.
Na verdade, somente a letra (a) está correta, respondendo à questão.
Resposta
a) O momento angular do elétron em torno do núcleo do átomo de hidrogênio seja igual a .