Partícula no Poço Finito
Produzido por Bruno SoaresTeoria
Introdução
Existem dois jeitos de se analisar o poço que captura elétrons, pra facilitar alguns cálculos a gente considera que a energia fora do poço tem potencial infinito e podemos analisar mais fácil o que acontece com o elétron capturado. Na prática o que acontece é que a energia do lado de fora do poço não é infinita, e com isso o que será que muda pra gente?
Já te digo que vamos usar a equação de Schrödinger, e caso você não esteja super familiarizado com ela vamos olhar um pouco pra ela e definir cada termo, tá?
Equação de Schrödinger independente do tempo:
Onde:
é a constante reduzida de planck que tem a seguinte relação:
é a função de onda independente do tempo.
é o potencial de cada região.
é a massa da partícula.
é a energia da partícula.
E se a energia em volta da caixa não for infinita?
A energia infinita na verdade é mais uma abstração do que uma realidade. A energia é sempre finita.
Graficamente nós temos:
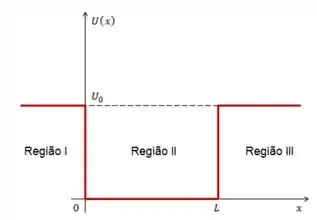
O problema de uma partícula num poço de potencial finito se descreve matematicamente por:
Onde:
A região I é para .
A região II dentro do poço é para
A região III, fora do poço também é para
Tem dois casos possíveis que estamos interessados. O primeiro é .
Neste caso, temos apenas uma partícula livre que não vai estar presa no poço. A energia dela é suficiente pra ela estar acima das barreiras.
Ela sendo uma partícula livre, seus níveis de energia não serão quantizados: Eles serão contínuos.
Energia da partícula dentro do poço
Agora vamos para o segundo caso:
Vamos olhar inicialmente para a região II, no interior do poço de potencial, onde .
Vamos ver como vai ficar a equação?
Rearrumando os coeficientes a gente vai ter:
E pra facilitar a nossa vida vamos chamar de o multiplicador da função de onda, o que vai nos ajudar a encontrar uma solução
Daí rearrumando temos:
A solução tem a forma:
Onde o índice representa em qual região a solução é pensada.
Nesse caso, não é nula em , então não é nulo. Nós ainda não sabemos as condições de contorno a serem aplicadas.
Energia da partícula fora do poço
Fora do poço de potencial, nas regiões e , a energia potencial é uma constante, e a Equação de Schrödinger independente do tempo é:
Vamos tentar chegar em algo parecido com o que foi feito pra dentro do poço, uma EDO com solução característica.
Rearrumando os termos e invertendo o sinal, temos:
E de novo pra facilitar a solução vamos chamar a galera que multiplica a função de onda de:
E aí teremos a equação menorzinha dessa forma:
Onde:
A solução dessa equação vai ser a combinação linear de duas exponenciais.
e são constantes cujo valor varia dependendo se estamos na região I ou na região III.
Análise da Função de Onda
Pra gente analisar as condições de contorno vamos lembrar que temos 3 regiões
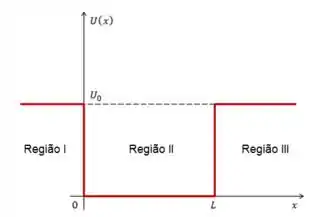
E temos que fazer a compatibilização das funções nessas 3 regiões, será possível? Vamos analisar fora do poço primeiro, onde a equação é:
No caso da região I, temos :
A medida que , o segundo termo o que não pode acontecer pois a função de onda não seria normalizável, logo, nessa região.
OBS: O termo normalizar pode soar estranho, mas significa que vamos fazer uma distribuição normal das probabilidades da função. Caso a função tenha um pico a gente consegue fazer essa distribuição normal, porém quando a função tende ao infinito isso não é possível e toda função de onda deve ser normalizável.
No caso da região III onde :
A medida que , o primeiro termo o que não pode acontecer pois a função de onda não seria normalizável também, logo, nessa região.
As funções de onda então são:
Agora vem o problema. A função de onda tem que ser contínua em todo o eixo , e por isso as condições de contorno ficariam algo do tipo:
E podemos resumir que em cada caso nossa função de onda é:
Teríamos que resolver uma equação onde uma exponencial é igual a uma soma de senos e cossenos, e isso não tem solução simples. Nós ganhamos mais duas condições dizendo que a derivada de também tem que ser contínua, mas de novo isso não tem soluções simples.
As equações que representariam condições de contorno vão fazer com que os estados possíveis dentro do poço sejam quantizados, sendo que fora do poço eles vão ser exponenciais que morrem depois de um tempo.
Análise Gráfica da Função de Onda
Já que a compatibilização das equações não é o melhor caminho vamos focar em aprender como se comportam os gráficos dessa função.
Dentro do poço existem vários níveis de energia e a gente vai usar um índice pra definir esses níveis, sendo o estado fundamental do elétron.
E se por acaso o seu professor te pedir pra esboçar o gráfico de algum nível energético dentro do poço, lembre se o seguinte:
O número de picos do gráfico é proporcional ao nível de energia
Só vamos esboçar o gráfico da partícula dentro do poço, então a parte exponencial da função não vai aparecer por aqui.
Então se temos 1 pico, se , temos dois picos no gráfico e por aí vai.
Então vamos esboçar o gráfico dos níveis 1, 2 e 3 dentro do poço.
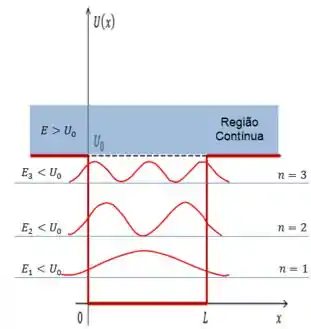
Eu representei apenas níveis, mas podem haver mais ou menos. A única regra aqui é que sempre tem que haver pelo menos um nível possível dentro do poço.
Uma observação importante é que esses níveis não são os mesmos que para uma partícula confinada.
Teoricamente a gente pode resumir a energia no poço finito com as seguintes afirmações
- A função de onda não é zero fora do poço. Ela decai exponencialmente.
- Quando , a energia e o estado do sistema são quantizados.
- Quando , a partícula vira o equivalente a uma partícula livre, e sua energia varia continuamente.
Bora pros exercícios?