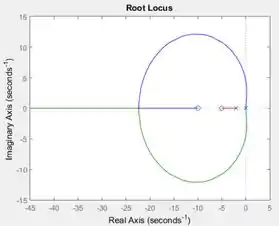
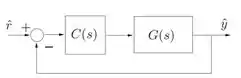
Considere um sistema de controle a tempo contínuo com realimentação unitária de acordo com a figura abaixo, na qual a planta é representada pela função de transferência
- Considerando um controlador , esboce o lugar das raízes e determine os valores de para os quais o sistema em malha fechada seja estável.
- Para o controlador do item anterior, determine o parâmetro de modo que o sistema em malha fechada possua dois polos complexos conjugados com fator de amortecimento igual a .
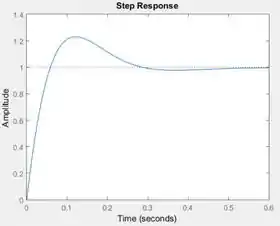
- Utilizando uma rotina computacional, obtenha a resposta ao degrau para o sistema em malha fechada, empregando o parâmetro encontrado no item anterior.
Passo 1
O enunciado nos dá uma função de transferência e nos pede para esboçar o lugar das raízes, determinar a faxa de valores do ganho em que o sistema é estável, encontrar o valor de que dê um fator de amortecimento igual a e, usando o encontrado, determinar a saída do sistema para o degrau unitário.
Para plotar o lugar das raízes de no MATLAB e resolver a letra a do exercício, usaremos a função . A partir do lugar das raízes plotado, resolveremos as letras a e b, achando os valores de no próprio gráfico. Com a resposta da letra b, faremos a letra c, gerando o sistema em malha fechada por meio do comando e plotando a resposta ao degrau unitário usando a função .
Passo 2
O primeiro passo é definir no MATLAB, usando a função , que tem a sintaxe:
A função tem como entrada dois vetores, o primeiro contendo os coeficientes do polinômio do numerador da função de transferência (representado por ) e outro contendo os coeficientes do polinômio do denominador (representado por ). retorna um objeto representando a função de transferência, que será armazenada em .
Contudo, repare que o numerador e o denominador de estão fatorizados. Para definirmos , vamos dividi-la em duas partes, e , de forma que :
Vamos começar definindo em um script novo do MATLAB, cujo numerador é e o denominador é . Vamos criar duas variáveis contendo os coeficientes dos polinômios de . A primeira variável representará os coeficientes do polinômio do numerador e será chamada de . A segunda variável será um vetor chamado e terá os coeficientes do polinômio do denominador. Após criar as duas variáveis de entrada de , digite o comando :

Desta forma, a função de transferência é criada e armazenada na variável
Vamos fazer a mesma coisa para :

Os vetores e contêm os coeficientes dos polinômios do numerador e do denominador de , respectivamente. Com a função , cria-se a funções de transferência .
Finalmente, para definir , inclua em seu código o produto abaixo:
![]()
Execute o programa para ver a cara de :

Passo 3
Após definir , podemos resolver a letra a do exercício usando a função para plotar o lugar das raízes. tem a sintaxe:
A função tem como entrada uma função de transferência criada a partir do comando (no nosso caso, é a variável ). Ao executarmos o programa, gera um gráfico com o lugar das raízes da função de transferência.
Adicione no seu script o comando:
![]()
Ao executar o programa, você terá o gráfico do lugar das raízes de :
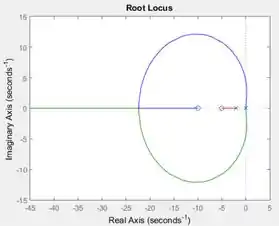
Passo 4
Podemos encontrar a faixa de valores que pode assumir no gráfico gerado no passo . Para isto, devemos relembrar o critério de estabilidade: uma malha de controle é estável se as raízes forem números reais negativos ou se forem números complexos com a parte real negativa. No lugar das raízes, isso significa que as raízes devem estar à esquerda do eixo vertical.
Isso quer dizer que, para encontrarmos os valores do ganho que garantem a estabilidade, devemos analisar os ramos que cruzam o eixo vertical. Logo, no nosso gráfico, a área de interesse é essa aqui:
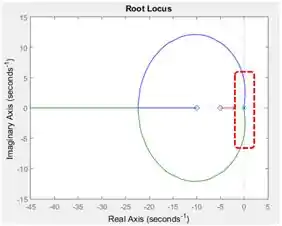
Por isso, recomendo você ampliar o gráfico, dando um zoom nessa região, pra ver bem certinho os polos e os ramos. Você pode dar o zoom clicando no botão destacado em vermelho abaixo:
Para ver os valores de ganho, selecione o botão “Data Cursor” (destacado em azul acima) e clique sobre um dos ramos. Aparecerá um quadradinho preto com uma janelinha contendo informações sobre na naquele ponto:
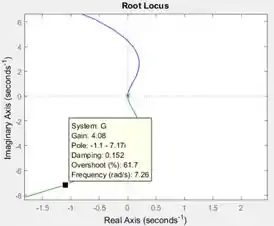
O dado “Gain” é o que nos interessa para responder à letra a. Ele representa o ganho nesse ponto. Se você arrastar o quadradinho até um xizinho, que representa um polo, você verá que quando o cursor estiver sobre o polo. Logo, quanto mais perto do polo, menor o .
O polo bem na fronteira da estabilidade são polos iguais a . Nesses polos, e quando nos afastamos deles, aumenta. O valor de em um ponto bem em cima do eixo vertical é o valor mínimo que tem que ter para que o sistema seja estável. O ganho pode assumir qualquer valor acima desse mínimo, pois o restante do lugar das raízes encontra-se à esquerda do eixo vertical.
No seu gráfico do lugar das raízes, clique sobre um ponto bem em cima do eixo vertical, para encontrar o valor mínimo de :
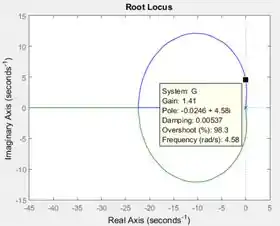
Para que o sistema em malha fechada seja estável, . Letra a respondida ;)
Passo 5
A partir do gráfico do lugar das raízes, vamos resolver a letra b do exercício, que pede para encontrarmos o ganho para termos um fator de amortecimento igual a .
No gráfico do lugar das raízes do MATLAB, clique sobre os ramos para ver as propriedades da função de transferência no ponto onde você clicou. Aqui, além do parâmetro “Gain”, que nos dá o valor de , vamor ver o parâmetro “Damping”, que dá o fator de amortecimento.
Arraste o quadradinho preto que apareceu onde você clicou até encontrar um ponto onde o parâmetro “Damping” seja igual a :
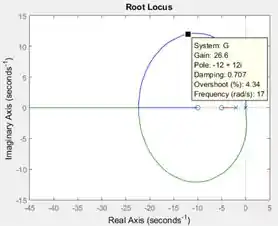
Temos que um ganho nos dá um fator de amortecimento igual a . Letra b resolvida ;D
Passo 6
A letra c pede para encontrarmos a resposta do sistema em malha fechada para um degrau unitário, considerando o ganho encontrado na letra b. Para isto, usaremos o comando , que tem a sintaxe:
A função plota o gráfico da resposta ao degrau unitário de , que é uma função de transferência criada usando o comando .
Contudo, precisamos aplicar no sistema em malha fechada, como o diagrama do enunciado:
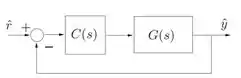
Para criar um sistema em malha fechada no MATLAB, usamos o comando , que tem a sintaxe:
O comando tem como entrada duas funções de transferência e retorna a função de transferência equivalente ao diagrama de blocos abaixo:
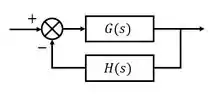
A primeira entrada de é a função de transferência da parte de cima do diagrama e a segunda entrada, é a função de transferência da parte de baixo.
No caso do exercício, quando usarmos a função , teremos que a primeira entrada é e a segunda entrada é , pois se trata de um sistema com realimentação unitária.
Insira no seu código as duas linhas abaixo:
![]()
Na primeira linha, definimos o ganho encontrado na letra b.
Na segunda linha, usamos o comando para plotar a resposta ao degrau do sistema com realimentação unitário, modelado por meio do comando .
Execute o programa e você terá a resposta da letra c.