Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Introdução à Dinâmica de Corpos Rígidos

Ver Todos os Exercícios

Teoria

Introdução

Até agora estudamos o movimento de corpos rígidos sem nos preocuparmos com o que causa esses movimentos.

Carros de corrida, por exemplo, são submetidos a forças muito intensas quando ele começa a acelerar:

Essas forças precisam ser calculadas e levadas em consideração quando se projeta a estrutura deste tipo de carro.

Porém, quando levamos em consideração o tamanho e a forma de um corpo, surgem forças que podem provocar translação e rotação.

Então, a partir de agora vamos estudar as consequências disso para o movimento do corpo. Mas será que o nosso corpo aceita de boa ser rotacionado por uma força?

Para responder esta pergunta vamos estudar o que chamamos de momento de inércia!!!

Momento de Inércia

O momento de inércia ( I ) é uma grandeza que mede a resistência de um corpo a sofrer uma rotação. Ou seja, quanto maior o momento de inércia mais difícil será girar o corpo. Para calcular, passamos um eixo z pelo centro de gravidade do um corpo e calculamos o momento que cada pedacinho de massa ( d m ) deste corpo faz com relação ao eixo:

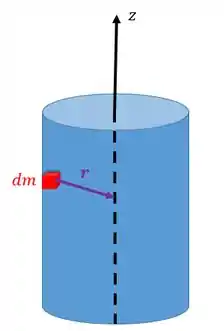
O momento de inércia vai ser calculado pela seguinte integral:

I = ∫ r 2 d m

Repare que r é o braço de alavanca do momento. A unidade do momento de inércia é k g . m 2 .

Atenção: esta fórmula é válida para calcular o momento de inércia com relação a um eixo que passe pelo centro de gravidade.

Se derivarmos ambos os lados da equação do momento de inércia, temos:

d I = r 2 d m

Essa equação também nos será útil!!!

Se um corpo possuir densidade ( ρ ) variável, cada pedacinho de massa ( d m ) do corpo vai ter:

d m = ρ d V

Ou seja, cada pedacinho de massa do corpo vai poder ser representado em função da densidade ( ρ ) e do volume ( V ) do corpo. Assim, ficamos com a seguinte integral:

I = ∫ r 2 ρ d V

Quando a densidade for constante, podemos tirar da integral e teremos que o momento de inércia vai depender da geometria do corpo:

I = ρ ∫ r 2 d V

Como estamos tratando de corpos tridimensionais, o volume vai depender da dimensão x , y e z de cada um daqueles pedacinhos:

d V = d x d y d z

Opa, teríamos então uma integral tripla!!!

Calma! Vamos ver maneiras de usar integral simples para resolver problemas que tenham corpos simétricos.

  1. Casca Elementar: neste método você tem que criar uma casca de espessura infinitesimal d y , raio r = y e altura z :

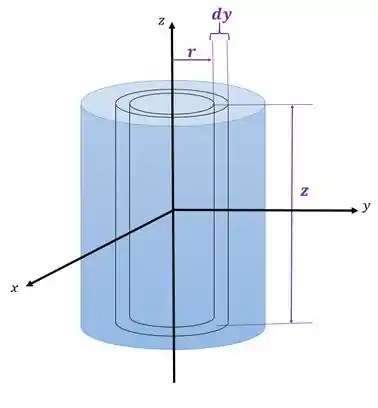
    2. Então, vamos ter que o volume será:

    d V = 2 π y z d y

    Agora é só substituir isso na integral:

    I = ∫ r 2 ρ d V   →         I = ∫ y 0 y f r 2 ρ 2 π y z d y

  2. Disco Elementar: neste método vamos fazer um disco com raio y e espessura infinitesimal d x :

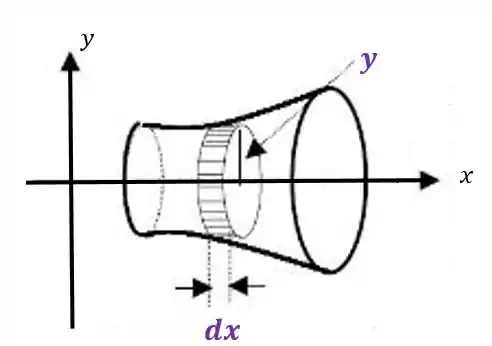
Observe que o raio e a espessura mudam conforme o eixo que a corpo está!!!

Neste método, o volume fica:

d V = π y 2 d x

Mas não podemos substituir isso direto na integral. Antes temos que calcular o momento de inércia somente do disco que criamos.

Repare que o disco que criamos é um cilindro com uma espessura beeem pequena, certo? Então, o momento de inércia do disco que criamos vai ser sempre igual ao momento de inércia de um cilindro ao longo de um eixo longitudinal (o eixo que percorre a maior dimensão do corpo):

I = m R 2 2

O momento de inércia de um cilindro ao longo do seu eixo longitudinal será sempre calculado por essa equação aí em cima, beleza?

Agora, como o nosso cilindro tem uma espessura bem pequenininha, temos que derivar essa equação aí:

d I = d m R 2 2

Repare que o raio é constante em um cilindro, por isso a única coisa que derivamos é a massa.

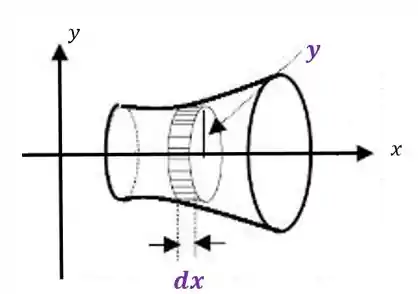
R pela variável do eixo onde está o raio. Veja nosso exemplo:

O raio do disco elementar está no eixo y e varia ao longo do comprimento do corpo. Neste caso, o momento de inércia do elemento infinitesimal d I será:

d I = d m R 2 2       →         d I = d m y 2 2

É só substituir o raio R pela variável que representa o raio na nossa figura, que neste caso foi a variável y !!!!

Agora é só lembrar que d m é:

d m = ρ d V

E quando estamos usando o método do disco elementar d V é:

d V = π y 2 d x

Então:

d I = d m y 2 2   →     d I = ρ π y 2 d x ( y 2 ) 2

Depois é só integrarmos de ambos os lados:

∫ d I = ∫ ρ π y 4 d x 2

Vamos ter que:

I = ∫ ρ π y 4 d x 2  

A questão vai te dar a equação que descreve o corpo e você vai conseguir escrever y em função de x para poder resolver a integral.

Teorema dos Eixos Paralelos

E se quisermos calcular o momento de inércia com relação a um eixo que não passa pelo centro de gravidade do corpo? Imagina uma placa circular que tem o seu centro de gravidade G no meio da peça:

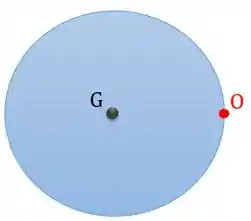
Como fazemos para calcular o momento de inércia com relação a um eixo z perpendicular ao plano da figura e que passa pelo ponto O ?

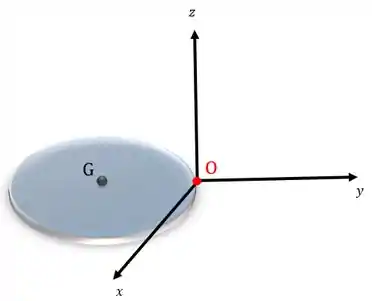
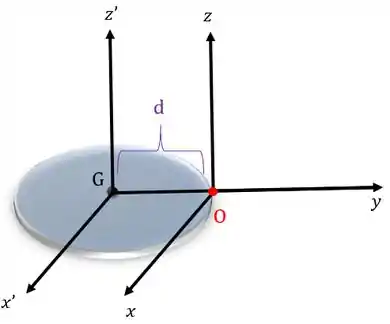
Se sabemos o momento de inércia com relação ao eixo que passa pelo centro de gravidade ( I G ) do corpo, então podemos achar o momento de inércia com relação a qualquer eixo paralelo através do que chamamos teorema dos eixos paralelos:

I = I G + m d 2

Onde, m é a massa do corpo e d é a distância entre os eixos paralelos.

Raio de Giração

O raio de giração ( k ) é uma grandeza que permite calcularmos o momento de inércia com relação a um eixo. Se tivermos o raio de giração k de um eixo e a massa m de um corpo, então o momento de inércia I será:

I = m k 2

Se tivermos o momento de inércia I e a massa do corpo m , é podemos calcular o raio de giração:

k = I m

A unidade do raio de giração é a unidade de comprimento.

Corpos Compostos

Se um corpo for formado por várias formas diferentes (como barras, discos, etc), o momento de inércia do corpo todo com relação a um eixo pode ser determinado somando o momento de inércia com relação a este mesmo eixo de cada uma dessa partes que compõe o corpo.

Atenção: se o corpo tiver um furo, podemos calcular o momento de inércia do corpo inteiro e subtrair o momento de inércia só do furo.

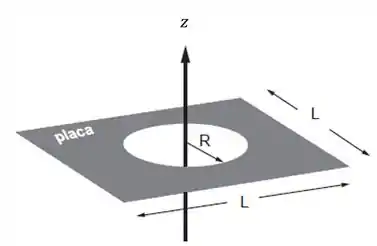
Neste exemplo, podemos calcular o momento de inércia do quadrado de lado L e subtrair o momento de inércia do círculo de raio R , ambos os momento de inércia calculados com relação ao eixo z .

Quando temos corpos compostos por formas conhecidas, podemos usar o momento de inércia tabelado para facilitar a vida. Aqui tem uma tabela de momento de inércia para os corpos mais comum:

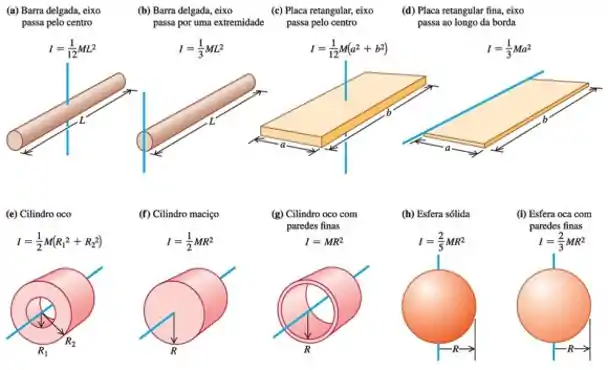
Beleza?

Vamos fazer uns exercícios para fixar essas coisas!!!

Teorema dos Eixos Paralelos

Raio de Giração

Corpos Compostos

Exercícios Resolvidos

Exercício Resolvido #1

R. C. Hibbeler, Dinâmica: Mecânica para Engenharia, 10º ed. SP: Prentice Hall, 2005, pp. 317-17.8

O cilindro sólido tem raio R e altura h. O material de que ele é feito tem uma densidade que varia com a distância r ao centro de acordo com a expressão ρ = k + a r 2 , onde k e a são constantes. Determine a )   a massa do cilindro e b ) seu momento de inércia em relação ao eixo z .

Passo 1

Para resolver este problema vamos usar o método da casca elementar, ou seja, vamos criar uma casca dentro do nosso cilindro com altura z = h , raio y = r e uma espessura infinitesimal d y = d r :

Com isso, sabemos que o nosso volume será:

d V = 2 π r h d r

Vamos começar calculando a massa deste cilindro e para isso temos que saber que:

m = ∫ d m

Mas não esqueça que:

d m = ρ d V

Opa, vamos substituir o nosso d V neste equação:

d m = ρ d V   →         d m = ρ 2 π r h d r

Então, a nossa integral vai ficar:

m = ∫ d m     →         m = ∫ ρ 2 π r h d r

Mas foi dito no enunciado que ρ = k + a r 2 , então:

m = ∫ ρ 2 π r h d r     →           m = ∫ ( k + a r 2 ) 2 π r h d r

Vamos passar as nossas constantes para o lado de fora da equação:

m = 2 π h ∫ ( k + a r 2 ) r d r

E agora vamos integrar ao longo do raio do cilindro de modo que a nossa casca vá de 0 a R :

m = 2 π h ∫ 0 R k r d r + ∫ 0 R a r 3 d r

m = 2 π h k r 2 2 | 0 R + a r 4 4 | 0 R

Vamos ter que:

m = 2 π h k R 2 2 + a R 4 4

Podemos arrumar um pouco mais isso:

m = 2 π h R 2 k 2 + a R 2 4

Passo 2

Nosso próximo passo é calcular o momento de inércia em relação ao eixo z . Para isso, temos que usar a equação do momento de inércia:

I z = ∫ r 2 d m

Mas sabemos que:

d m = ρ 2 π r h d r

Então:

I z = ∫ r 2 ρ 2 π r h d r

I z = 2 π h ∫ ρ r 3 d r

Sabemos também que:

ρ = k + a r 2

Então:

I z = 2 π h ∫ ( k + a r 2 ) r 3 d r

Podemos separa em duas integrais e integrar ao longo do raio:

I z = 2 π h ∫ 0 R k r 3 d r + ∫ 0 R a r 5 d r

I z = 2 π h k r 4 4 | 0 R + a r 6 6 | 0 R

Então, I z será:

I z = 2 π h k R 4 4 + a R 6 6

Podemos ajeitar isso um pouco mais:

I z = 2 π h R 4 k 4 + a R 2 6

Resposta

a ) m = 2 π h R 2 k 2 + a R 2 4

b )   I z = 2 π h R 4 k 4 + a R 2 6

Exercício Resolvido #2

R. C. Hibbeler, Dinâmica: Mecânica para Engenharia, 10º ed. SP: Prentice Hall, 2005, pp. 316-17.3

O cone circular reto é formado pela revolução, em torno do eixo x , da área cinza-escuro. Determine o momento de inércia I x e expresse o resultado em termos da massa total m do cone. Considere que o cone tem densidade constante ρ .

Passo 1

Para resolver este problema vamos usar o método do disco elementar, ou seja, vamos criar um disco dentro do nosso cone com raio y e uma espessura infinitesimal d x . Com isso, sabemos que o nosso volume será:

d V = π y 2 d x

Vamos começar calculando a massa deste sólido e para isso temos que saber que:

m = ∫ d m

Mas como se calcula esse elemento de massa infinitesimal d m ?

d m = ρ d V

Opa, vamos substituir o nosso d V neste equação:

d m = ρ d V   →         d m = ρ π y 2 d x

Então, a nossa integral vai ficar:

m = ∫ d m     →         m = ∫ ρ π y 2 d x

Vamos passar as nossas constantes para o lado de fora da equação:

m = π ρ ∫ y 2 d x

E agora vamos integrar ao longo da altura do cilindro de modo que o nosso disco percorra toda a altura do cone:

m = π ρ ∫ 0 h y 2 d x

Perceba que na figura foi dada a equação do cone:

y = r x h

Vamos substituir o y da nossa integral:

m = π ρ ∫ 0 h r x h 2 d x

Repare que r e h também são constantes:

m = π ρ r h 2 ∫ 0 h x 2 d x

Agora é só resolver:

m = π ρ r h 2 ∫ 0 h x 2 d x         →           m = π ρ r h 2 x 3 3 | 0 h

Então:

m = π ρ r h 2 h 3 3

Vamos ter que:

m = π ρ r 2 h 3

Como o enunciado pede o momento de inércia em função da massa m , vamos isolar ρ :

ρ = 3 m π r 2 h

Passo 2

Nosso próximo passo é calcular o momento de inércia em relação ao eixo x . Para isso, temos que calcular o momento de inércia do disco de espessura infinitesimal:

I x = ∫ r 2 d m

Mas sabemos que o momento de inércia de um cilindro em relação ao seu eixo longitudinal é:

I =   m R 2 2

Como o disco que criamos é um cilindro só que de espessura bem pequena, é só derivarmos o momento de inércia do cilindro que é sempre a mesma para o eixo longitudinal:

d I x = d m R 2 2

Repare que o raio R é constante, por isso só derivamos a massa.

Nós já sabemos que:

d m = ρ π y 2 d x

Então d I x vai ser:

d I x = ( ρ π y 2 d x ) R 2 2

Repare que o raio r = y do nosso disco varia conforme ele percorre toda a altura do cone, então:

d I x = ( ρ π y 2 d x ) y 2 2

Vamos ter que:

d I x = ρ π y 4 d x 2

No passo 1 achamos que ρ :

ρ = 3 m π r 2 h

Vamos ter que d I x :

d I x = 3 m π r 2 h π y 4 d x 2

Passo 3

Pronto! Agora é só integrarmos dos dois lados:

∫ d I x = ∫ 3 m π r 2 h π y 4 d x 2

Vamos tirar nossas constantes para fora da integral:

I x = 3 m π r 2 h π 2 ∫ y 4 d x

Repare que dá para simplificar essas constantes:

I x = 3 m 2 r 2 h ∫ y 4 d x

Nós sabemos que a equação do cone é: y = r x h

Então, a nossa integral ao longo da altura h será:

I x = 3 m 2 r 2 h ∫ 0 h r x h 4 d x

Vamos tirar as constantes para fora da integral e depois simplificar:

I x = 3 m 2 r 2 h r h 4 ∫ 0 h x 4 d x       →           I x = 3 m r 2 2 h 5 ∫ 0 h x 4 d x

Vamos ter que:

I x = 3 m r 2 2 h 5 x 5 5 | 0 h

I x = 3 m r 2 2 h 5 h 5 5

Vamos arrumar nossa resposta:

I x = 3 m r 2 10

Resposta

I x = 3 m r 2 10

Exercício Resolvido #3

R. C. Hibbeler, Dinâmica: Mecânica para Engenharia, 10º ed. SP: Prentice Hall, 2005, pp. 318-17.15

A roda consiste num anel fino de 10   k g e quatro raios feitos de barras delgadas, cada uma com com 2   k g . Determine o momento de inércia da roda em relação a um eixo que é perpendicular à página e passa pelo ponto A . Suponha que as barras e o anel são homogêneos.

Passo 1

Para resolver este problema vamos ter que aplicar o teorema dos eixos paralelos. Repare que temos duas barras e um anel, então vamos calcular o momento de inércia deles com relação ao eixo que passa pelo centro de gravidade G .

O momento de inércia com relação a um eixo que passa pelo centro de gravidade é:

I G = ∫ r 2 d m

Mas sabemos que:

m = ∫ d m

E repare que no enunciado foram dadas as massas m de cada elemento que compõe o corpo. Como o raio é constante, podemos dizer que o momento de inércia com relação ao eixo que passa pelo centro de gravidade é:

I G = m r 2

O momento de inércia de um anel fino é tabelado:

I G a n e l = m r 2

Onde, r é o raio do anel. Então, no nosso caso teremos:

I G a n e l = m a n e l r 2

Temos que a massa do anel é 10   k g e a distância do anel até o eixo é igual ao valor do raio de 0,5   m :

I G a n e l = 10 ( 0,5 ) 2

I G a n e l = 2,5   k g . m 2

Passo 2

Para as barras vamos fazer a mesma coisa. Sabemos que o momento de inércia de uma barra delgada também é tabelado e vale:

I G b a r r a = m L 2 3

Como estamos considerando o quatro barras, o comprimento de cada barra será de igual ao valor do raio do anel:

L = r = 0,5   m

Então:

I G b a r r a = m b a r r a r 2 3

A massa da barra vale 2   k g :

I G b a r r a = ( 2 ) ( 0,5 ) 2 3

I G b a r r a = 0,167   k g . m 2

Então, o momento de inércia com relação ao eixo que passa pelo centro de gravidade da peça é igual a soma do momento de inércia com relação ao mesmo eixo de cada parte que compõe a figura:

I G T o t a l = I G a n e l + 4 I G b a r r a

Não esqueça que temos quatro barras e só calculamos o momento de inércia para uma delas:

I G T o t a l = 2,5 + 4 ( 0,167   )

I G T o t a l = 3,168   k g . m 2

Passo 3

Nosso próximo passo é calcular o momento de inércia em relação ao eixo perpendicular à figura e que passa pelo ponto A . Para isso, temos que saber a distância d entre os eixos paralelos:

d = r = 0,5   m

Então, vamos usar o teorema dos eixos paralelos:

I A = I G + m d 2

I A = I G T o t a l + m a n e l d 2 + 4 m b a r r a d 2

Lembrando que a massa do anel é 10   k g e a massa da barra é de 2   k g :

I A = 3,168 + 10 ( 0,5 ) 2 + 4 ( 2 ) ( 0,5 ) 2

I A = 7,67   k g . m 2    

Resposta

I A = 7,67   k g . m 2    

Exercício Resolvido #4

R. C. Hibbeler, Dinâmica: Mecânica para Engenharia, 10º ed. SP: Prentice Hall, 2005, pp. 316-17.5

O sólido mostrado na figura é formado pela revolução da área cinza-escuro ao redor do eixo y . Determine o raio de giração k y . O peso específico do material é γ = 380   l b / p é 3 .

Passo 1

Sabemos que para calcular o raio de giração temos que usar a seguinte fórmula:

k = I m

Onde, I é o momento de inércia e m é a massa. Então, vamos começar nosso problema achando a massa deste corpo.

Para resolver esta questão vamos usar o método do disco elementar, ou seja, vamos criar um disco dentro do nosso sólido de raio x e uma espessura infinitesimal d y . Com isso, sabemos que o nosso volume será:

d V = π x 2 d y

Vamos começar calculando a massa deste cilindro e para isso temos que saber que:

m = ∫ d m

Mas como se calcula esse elemento de massa infinitesimal d m ?

d m = ρ d V

Opa, vamos substituir o nosso d V neste equação:

d m = ρ d V   →         d m = ρ π x 2 d y

Então, a nossa integral vai ficar:

m = ∫ d m     →         m = ∫ ρ π x 2 d y

Vamos passar as nossas constantes para o lado de fora da equação:

m = π ρ ∫ x 2 d y

E agora vamos integrar ao longo da altura do sólido ( h = 3   p o l ) de modo que o nosso disco percorra toda a sua altura:

m = π ρ ∫ 0 3 x 2 d y