Movimento em Relação a Eixos que Giram
Teoria
Introdução
Até agora usamos o movimento relativo para analisar o movimento de pontos que pertencem a um mesmo corpo rígido ou de pontos localizados em corpos que são articulados entre si.
Imagina agora que você está dentro de um trem...
E bem no momento que ele está fazendo uma curva, você resolve levantar...
O que acontecerá com o seu movimento quando você se move sobre o trem que está numa trajetória circular, ou seja, fazendo uma rotação e também está realizando uma translação?
É justamente isso que vamos aprender neste capítulo: o que muda quando queremos determinar o movimento relativo de corpos que realizam tanto translação quanto rotação ao mesmo tempo!
Velocidade Relativa
Neste tipo de questão sempre teremos dois corpos, um que será nosso referencial e outro que temos que analisar o seu movimento.
Quando temos dois corpos que não pertencem ao mesmo corpo rígido e que realizam tanto rotação (uma curva, por exemplo) quanto translação, vamos usar a seguinte equação para relacionar as suas velocidades:
Onde:
- é o vetor velocidade absoluta do corpo que está se movendo (corpo ) com relação ao corpo que está nosso referencial (corpo );
- é o vetor velocidade absoluta do corpo onde está nosso referencial, ou seja, é de onde estamos observando o movimento do corpo ;
- é o vetor velocidade angular do corpo , onde está o nosso sistema de referência.
- é o vetor posição do corpo com relação a , ou seja, é a posição de com relação ao eixo de referência fixo no corpo ;
- é a velocidade relativa do corpo com relação ao corpo .
Para entender melhor isso, vamos usar o exemplo do nosso trem.
Imagina que você está em um trem viajando pela Europa... 
E bem no momento que o trem está fazendo uma curva, você resolver ir até o banheiro:
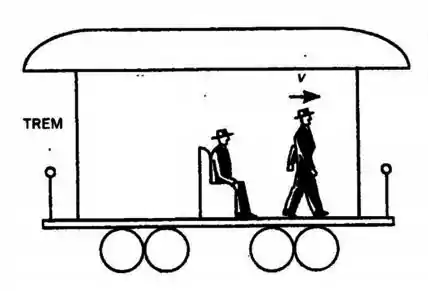
Repare que o trem realiza movimento de rotação e translação. Como você está dentro do trem, você realiza os mesmos movimentos. Então, já somos capazes de identificar quem é o nosso referencial e quem está realizando o movimento relativo: a pessoa realiza o movimento relativo e o trem é onde está o nosso referencial:
- Corpo Pessoa
- Corpo Trem
Então, vamos colocar nosso eixo fixo no trem:
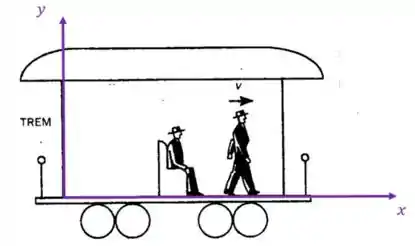
Identificado quem é o corpo e quem é o corpo , podemos dizer que:
Como o trem está fazendo uma curva, ele possui uma velocidade angular.
- Velocidade angular do trem
- é a aceleração do corpo , ou seja, quem realiza o movimento relativo (no nosso exemplo, é a pessoa andando no trem);
- é a aceleração do corpo que é onde está o nosso referencial;
- é a aceleração angular do corpo , ou seja, onde está o eixo fixo (no nosso exemplo seria a aceleração angular do trem);
- é o mesmo vetor posição da equação da velocidade, ou seja, a posição do corpo com relação a ;
- também é a mesma velocidade angular da equação da velocidade;
- é a mesma velocidade relativa de com relação a ;
- é a aceleração relativa que o corpo tem com relação ao corpo . No nosso exemplo seria a aceleração que a pessoa tem com relação ao trem que está também em movimento.
E o vetor posição ? É a posição da pessoa com relação ao nosso eixo fixo:
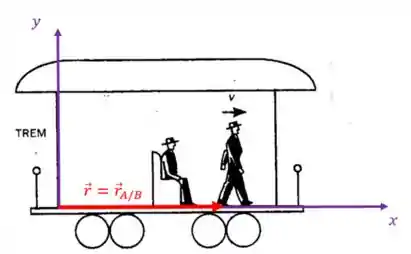
A seta do vetor sempre chega no corpo e começa na origem do eixo fixo! 
Quando você começa a andar dentro do trem, adquire uma velocidade em relação ao trem, certo? Esta vai ser a velocidade relativa da pessoa com relação ao trem:
Beleza?
Então, nesses tipos de questões sempre temos que localizar quem está realizando o movimento relativo e onde está o nosso eixo fixo. Depois é só pegar a nossa nova equação da velocidade relativa e identificar quem é cada termo da equação de acordo com a situação que temos (igual fizemos nesse exemplo).
Aceleração relativa
A equação que relaciona as acelerações do corpo e do corpo é:
Calma, não se assuste!!! Essa equação é um pouco trabalhosa, mas não é difícil!
Vamos ver o que cada termo da equação significa:
Aceleração de Coriolis
A aceleração de Coriolis corresponde ao termo lá da equação da aceleração relativa que acabamos de ver. Esse nome estranho é o sobrenome do primeiro engenheiro que determinou esta aceleração.
Mas o que quer dizer esta aceleração? Ela representa a diferença na aceleração do corpo medida no sistema fixo e em rotação.
A aceleração de Coriolis tem direção perpendicular ao vetor e ao vetor velocidade angular . O seu sentido é definido pela regra da mão direita para produto vetorial como vimos anteriormente.
Agora que você sabe tudo sobre movimento relativo com eixos girantes, tem o direito de ganhar a sua passagem para embarcar nos exercícios:
Partiu?
Velocidade Relativa
Aceleração relativa
Aceleração de Coriolis
Exercícios Resolvidos
Exercício Resolvido #1
J.L. Meriam e L.G. Kraige, Mecânica para Engenharia, Estática, 6º ed. RJ: LTC, 2012, pp. 294-5/164
Ao contornar uma curva sem inclinação lateral a uma velocidade constante de , o centro do vagão ferroviário segue uma trajetória circular de raio . O eixo longitudinal do vagão permanece tangente ao círculo. Determine a velocidade absoluta de uma pessoa que caminha na velocidade constante de 1,5 m/s em relação ao vagão quando ele está nos pontos e . Utilize os eixos presos ao vagão como indicado.
Passo 1
Quando temos o movimento relativo de corpos que realizam movimento de rotação e translação ao mesmo tempo, vamos usar a seguinte equação:
O próximo passo é identificar quem está realizando o movimento relativo. Neste caso, é a pessoa. Então, a velocidade corresponde a velocidade absoluta da pessoa:
E é justamente o que queremos saber!
A velocidade é a velocidade absoluta do trem:
Que passando para , temos:
Como o trem anda para a esquerda, o vetor velocidade será:
Como o trem está realizando um movimento circular, a sua velocidade angular pode ser calculada assim:
Sabemos que a velocidade angular está sempre no eixo e como o trem está andando para a esquerda, então a velocidade angular é positiva:
E a velocidade relativa é a velocidade da pessoa com relação ao vagão do trem. Repare que a pessoa caminha da direita para a esquerda, ou seja, no sentido negativo do eixo :
Passo 2
Vamos calcular primeiro a velocidade absoluta da pessoa quando ela está no ponto . Repare que quando ela está no ponto , a sua posição é:
Então, a nossa equação fica:
Vamos resolver o produto vetorial:
Então:
Passo 3
Agora, vamos calcular a velocidade absoluta da pessoa quando ela está no ponto . Repare que quando ela está neste ponto, a sua posição é:
Então, a nossa equação fica:
Vamos resolver o produto vetorial:
Então:
Passo 4
Por último vamos calcular a velocidade absoluta da pessoa quando ela está no ponto . Repare que quando ela está neste ponto, a sua posição é:
Então, a nossa equação fica:
Essa é moleza, né?
Resposta
Exercício Resolvido #2
R. C. Hibbeler, Dinâmica: Mecânica para Engenharia, 10º ed. SP: Prentice Hall, 2005, pp. 303-16.135
Enquanto a ponte giratória está fechando com uma velocidade angular de , um homem corre ao longo da pista a uma velocidade constante de , relativamente à pista. Determine a velocidade e a aceleração do homem, no instante em que .
Passo 1
Como se trata de corpos que realizam movimentos de rotação e translação ao mesmo tempo, vamos utilizar a seguinte equação para a velocidade:
Nosso próximo passo é identificar onde ocorre o movimento relativo. Perceba que enquanto a ponte gira, o homem se move por ela. Então, o homem que realiza o movimento relativo. Agora vamos organizar a nossa equação.
A velocidade é a velocidade absoluta de quem realiza o movimento, que no nosso caso é o homem:
Essa é a primeira coisa que precisamos descobrir!
A velocidade é a velocidade da ponte. Mas repare que a ponte apenas gira, então a sua velocidade é zero:
A velocidade angular da ponte foi dada, mas repare que ela gira no sentido anti-horário, então o vetor é positivo:
O vetor posição do homem com relação ao eixo será:
E enfim, a velocidade relativa é a velocidade que o homem tem com relação a ponte. Repare que ele está correndo no sentido negativo do eixo :
Passo 2
Agora que identificamos o que é cada coisa na nossa equação, é só substituirmos:
Vamos resolver o produto vetorial separado:
Substituindo isso aí na nossa equação, vamos ter que:
O módulo da velocidade vai ser:
Passo 3
Agora vamos fazer a análise da aceleração. Para isso, vamos usar a seguinte equação:
A aceleração do homem é:
Lembra que vimos que a ponte não tem velocidade, portanto ela também não terá aceleração:
A aceleração angular da ponte também é zero, porque ela gira a velocidade constante:
Repare que os vetores posição , velocidade angular e velocidade relativa não mudam.
A aceleração relativa também é zero, porque o homem corre com velocidade constante :
Então, vamos ter que:
Já sabemos que:
Então:
Esse produto vetorial vai ficar:
O outro produto vetorial que precisamos é:
Substituindo isso na nossa equação, vamos ter:
O seu módulo será:
Resposta
Exercício Resolvido #3
J.L. Meriam e L.G. Kraige, Mecânica para Engenharia, Dinâmica, 6º ed. RJ: LTC, 2012, pp. 294-5/159
O disco gira em torno de um eixo fixo através de com velocidade angular e aceleração angular no instante representado, nos sentidos indicados. O cursor se desloca na ranhura reta. Determine a velocidade e a aceleração absolutas de para o mesmo instante, quando , e .
Passo 1
Nosso primeiro passo é identificar onde ocorre o movimento relativo. Perceba que enquanto o disco gira em torno de , o cursor se move na ranhura. Então, o movimento relativo ocorre no cursor . Para a velocidade vamos usar a seguinte equação:
Repare que o disco apenas gira em torno do ponto , ou seja, só possui velocidade angular com relação a esse ponto, então:
A velocidade angular é sempre perpendicular à figura, ou seja, está no eixo . Como ela faz o disco girar no sentido anti-horário, a velocidade angular é positiva de acordo com a nossa convenção de sinais:
E o vetor posição ? Ela indica a posição do cursor medido a partir do eixo no instante mostrado na figura:
A velocidade relativa é a velocidade do cursor com relação ao eixo que gira:
Então, vamos ter que:
Vamos resolver esse produto vetorial aí:
Substituindo isso aí na nossa equação, vamos ter que:
Então, será:
Passo 2
Agora vamos fazer a análise da aceleração. Para isso, vamos usar a seguinte equação:
Lembra que vimos que o corpo não tinha velocidade no ponto , portanto ele também não terá aceleração:
A aceleração angular do disco estará sempre no eixo e como ela gira no sentido contrário da velocidade angular, ela é negativa:
Repare que os vetores posição , velocidade angular e velocidade relativa não mudam:
Já a aceleração relativa é a aceleração que o cursor possui e está posicionada no eixo :
Então, vamos ter que:
Vamos fazer cada produto vetorial separado:
- Já sabemos que:
- :
- :
- :
Pronto! Agora é só substituirmos:
Somando os termos de mesma componente, obtemos:
Resposta
Exercício Resolvido #4
J.L. Meriam e L.G. Kraige, Mecânica para Engenharia, Estática, 6º ed. RJ: LTC, 2012, pp. 295-5/171
Os carros e estão contornando as curvas com velocidades iguais de . Determine a velocidade que parece ter para um observador se deslocando e girando com o carro para o instante representado. A curvatura da estrada para o carro afeta o resultado? Os eixos estão fixos no carro .
Passo 1
Quando temos o movimento relativo de corpos que realizam movimento de rotação e translação ao mesmo tempo, vamos usar a seguinte equação:
O que queremos determinar é a velocidade que parece ter para um observador se deslocando e girando com o carro , ou seja, queremos calcular a velocidade relativa .
O próximo passo é identificar quem está realizando o movimento relativo. Neste caso, é o carro , já que o eixo está fixo no carro . Então, a velocidade corresponde a velocidade absoluta do carro :
Vamos passar esta velocidade para :
Repare que o carro se move no sentido positivo do eixo , então o vetor velocidade é:
Como a velocidade do carro é igual a velocidade do carro , então:
Porém, o carro se move no sentido positivo do eixo :
A velocidade angular pode ser calculada, já que ambos os carros realizam movimento circular. Mas repare que a velocidade angular a ser calculada é a do carro (onde está o eixo fixo):
A velocidade angular é positiva, porque devido a posição dos eixos , o sentido positivo do eixo é apontando para dentro da tela.
E o vetor posição é a distância do carro até o eixo que está fixo em :
Passo 2
Agora que definimos o que é cada coisa da nossa equação, vamos substituir:
Vamos resolver o produto vetorial:
Então:
Passo 3
A questão quer saber se ao mudar o raio de curvatura do carro vai alterar a velocidade relativa. A resposta é não, porque usamos o raio de curvatura para calcular a velocidade angular . Mas sempre calculamos a velocidade angular do corpo onde está o eixo fixo e não no corpo em que estamos analisando o movimento relativo.
Resposta
Exercício Resolvido #5
R. C. Hibbeler, Dinâmica: Mecânica para Engenharia, 10º ed. SP: Prentice Hall, 2005, pp. 304-16.140
Um brinquedo de um parque de diversões consiste em uma plataforma girante , que tem velocidade angular constante , e quatro barquinhas, , montadas na plataforma, que têm velocidade angular constante , medida relativamente à plataforma. Determine a velocidade e a aceleração do passageiro , na situação mostrada na figura.
Dados: ; .
Passo 1
Vamos começar calculando a velocidade do passageiro que está no ponto :
Primeiro temos que identificar o que é cada termo da nossa equação no problema que queremos resolver!
A velocidade é aquela velocidade que queremos saber, então ela corresponde a velocidade do passageiro que está no ponto . Então, para ficar mais intuitivo:
A velocidade é a velocidade de onde está o nosso referencial fixo, que é o próprio brinquedo (é onde tudo está acontecendo):
Mas repare que a plataforma só gira em torno do ponto , ou seja, ela só tem velocidade angular:
A velocidade angular que aparece na nossa equação também é a do brinquedo que está girando com no sentido anti-horário (positivo), então o vetor será:
O vetor posição pode ser obtido na figura:
Como o raio do movimento da cadeiras é de , então o vetor será:
O vetor velocidade relativa corresponde a velocidade que o passageiro tem com relação ao brinquedo. Mas repare que só temos a velocidade angular relativa:
Como a cadeira está girando no sentido anti-horário, essa velocidade angular é positiva e seu vetor é:
Passo 2
Mas como vamos achar o valor da velocidade relativa ()? Repare que se olharmos só para as cadeiras, vamos ver que elas estão fazendo um movimento circular e também transladando devido a rotação da plataforma do brinquedo.
Sabemos que:
Porém, a velocidade angular da cadeira vai ser a soma da velocidade angular relativa (que a cadeira tem com relação à plataforma do brinquedo) com a velocidade angular do próprio brinquedo:
O vetor posição do passageiro com relação ao centro da cadeira é:
Então:
Nossa matriz fica:
Passo 3
Agora sim podemos calcular a velocidade do passageiro:
Vamos resolver o produto vetorial primeiro:
Então:
Passo 4
Agora vamos calcular a aceleração do passageiro:
Vamos mais uma vez relacionar cada termo da equação com o que está acontecendo na situação do problema.
A aceleração corresponde a aceleração do passageiro e justamente o que queremos saber:
A aceleração angular do brinquedo , neste nosso caso, é nula. Isso porque no enunciado foi dito que a plataforma do brinquedo tem uma velocidade angular constante.
A velocidade angular continua a mesma da outra equação:
A velocidade relativa também continua a mesma:
E a aceleração relativa das cadeiras é zero também, porque a velocidade angular das cadeiras é constante.
Vamos fazer uma observação importante: no termo correspondente à aceleração de coriolis () não podemos usar a velocidade angular da plataforma, temos que fazer o produto vetorial com a mesma velocidade angular que usamos para achar a velocidade relativa:
)
Então, ao invés de usarmos a aceleração de Coriolis, vamos usar essa expressão aí de cima.
Então, nossa equação vai ficar:
Já sabemos que:
Então:
Vamos resolver os produtos vetoriais:
E:
Vamos ter que:
Resposta
Exercício Resolvido #6
R. C. Hibbeler, Dinâmica: Mecânica para Engenharia, 10º ed. SP: Prentice Hall, 2005, pp. 304-16.141
O bloco do mecanismo tem de ser deslocar na ranhura da barra . Se está se movendo a uma taxa constante , determine a velocidade angular e a aceleração angular da barra , na situação mostrada na figura.
Passo 1
Nesse tipo de questão, a primeira coisa que temos que fazer é posicionar o eixo que será móvel e aquele que será fixo.
Repare que o bloco se move ao longo da barra , então vamos posicionar o nosso eixo móvel () nesta barra onde ocorre o movimento:
Nosso eixo fixo () vai ser aquele que estamos acostumados:
Passo 2
Feito isso podemos começar a resolver nossa questão. Vamos começar pela barra que temos alguma informação sobre o seu movimento que é a barra . Repare que nesta barra o ponto gira em torno do ponto que é fixo, então vamos usar nossa velha conhecida equação:
A velocidade angular da barra foi dada e como está girando no sentido horário é negativa:
O vetor posição de com relação ao ponto é:
Agora é só fazermos o produto vetorial:
Passo 3
Nosso próximo passo é analisar a barra que é justamente a barra que a questão quer saber. Como nesta barra está o nosso eixo móvel, temos que usar a equação para eixos girantes:
Primeiro temos que identificar o que é cada termo da nossa equação com relação ao questão que queremos resolver!
A velocidade é a velocidade do ponto com relação ao referencial fixo. Mas repare que o ponto não se move ao longo do eixo, ele é fixo, logo sua velocidade é nula:
A velocidade angular que aparece na nossa equação é justamente o que a questão pede para determinamos. Repare que na figura que foi dada no enunciado já tem um sentido para a velocidade angular desta barra, então vamos só colocar o sentido que é negativo:
E o vetor ?
A velocidade relativa corresponde a velocidade que ponto tem quando ele se movimenta ao longo do eixo móvel. Como o ponto só pode se mover ao longo da barra , o vetor velocidade será:
Repare que a velocidade está apontando para baixo, porque a barra está girando no sentido horário o que faz o ponto se mova para baixo ao longo do eixo móvel.
Porém, antes de colocar na nossa equação temos que decompor o vetor velocidade relativa para o eixo fixo . Como não sabemos seu valor, vamos ter que:
Agora sim podemos substituir tudo que achamos na nossa equação:
Vamos resolver este produto vetorial:
Então, temos que:
Passo 4
Lembra que já achamos a velocidade do ponto antes:
Então, vamos substituir esse valor nessa equação que achamos:
Agora temos que separar as componentes e em duas equações:
Da primeira equação temos que:
Substituindo isso na segunda equação:
O resultado ter dado positivo indica que arbitramos o sentido correto para o vetor (graças a dica da figura hahaha). Então, temos que:
E a velocidade relativa será:
Passo 5
Agora vamos analisar a aceleração do ponto . Primeiro vamos usar a barra que é a barra que temos alguma informação sobre seu movimento. Repare que o ponto faz um movimento circular em torno do ponto que é fixo, então:
Foi dito no enunciado da questão que a barra se move a uma taxa constante, portanto sua aceleração angular é nula:
Então nos sobra:
E já sabemos que:
E:
Substituindo isso na nossa equação, temos que:
Passo 6
Mas não é a aceleração do ponto que a questão pede. O que queremos é a aceleração angular da barra . Então, vamos analisar o movimento nesta barra sabendo que é nela que está nosso eixo móvel.
A equação da aceleração com relação ao eixo móvel é:
Vamos mais uma vez relacionar cada termo da equação com o que está acontecendo na situação do nosso problema.
Como o ponto está fixo, ele não possui aceleração:
A aceleração angular da barra nós não sabemos, mas pela figura é possível ver que o seu sentido é horário:
A aceleração relativa corresponde a aceleração do ponto quando ele se move no eixo móvel. Como o ponto só pode se mover ao longo da barra , o vetor aceleração relativa será:
Precisamos decompor o vetor no eixo fixo :
Não esqueça que tem que decompor o vetor velocidade relativa (), cujo valor achamos no passo anterior, nos eixos também. Vai ficar assim:
E o restante dos termos nós já sabemos, então a nossa equação fica:
Vamos resolver cada um dos produtos vetoriais:
O próximo nós já tínhamos resolvido antes:
Então:
Vamos para o nosso último produto vetorial:
Agora, vamos substituir isso na nossa equação lá de cima:
Vamos dar aquela ajeitada na nossa equação:
Passo 7
Lembra que achamos um valor para a aceleração do ponto ?
Então, vamos substituir este valor na nossa equação:
Agora vamos separar as componentes e cada qual na sua equação:
Da segunda equação tiramos que:
Substituindo isso na primeira equação temos que:
Como o sinal deu negativo, significa que arbitramos o sentido contrário para a aceleração angular da barra . Como tínhamos arbitrado o sentido negativo, ela vai ser positiva:
Resposta
Exercício Resolvido #7
R. C. Hibbeler, Dinâmica: Mecânica para Engenharia, 10º ed. SP: Prentice Hall, 2005, pp. 304-16.144
Num dado instante, a barra tem velocidade angular e aceleração angular . Determine a velocidade angular e a aceleração angular da barra , nesse instante. O colar em está ligado por pino em e desliza em .
Passo 1
Nesse tipo de questão, a primeira coisa que temos que fazer é posicionar o eixo que será móvel e aquele que será fixo.
Repare que o colar em se move ao longo da barra , então vamos posicionar o nosso eixo móvel () nesta barra:
Nosso eixo fixo () vai ser aquele que estamos acostumados:
Passo 2
Feito isso podemos começar a resolver nossa questão. Vamos começar pela velocidade do ponto com relação ao eixo móvel, pois temos informações sobre o movimento da barra :
Primeiro temos que identificar o que é cada termo da nossa equação no problema que queremos resolver!
A velocidade é a velocidade do ponto com relação ao referencial fixo. Mas repare que o ponto é fixo, logo sua velocidade é nula:
A velocidade angular que aparece na nossa equação nós já sabemos que é positiva:
E o vetor ?
A velocidade relativa corresponde a velocidade do ponto quando ele se move no eixo móvel. Como o colar só pode se mover ao longo da barra , o vetor velocidade será:
Porém, antes de colocar na equação temos que decompor o vetor para o eixo fixo. Como não sabemos seu valor, vamos ter que:
Agora sim podemos substituir tudo que achamos na nossa equação:
Vamos resolver este produto vetorial:
Então, temos que:
Vamos guardar essa equação, pois não conseguimos avançar só com ela.
Passo 3
Temos que buscar outra forma de achar a velocidade do ponto . Para isso vamos usar a barra . Repare que nesta barra o ponto gira em torno do ponto que é fixo, então vamos usar nossa velha conhecida equação:
Não sabemos o valor da velocidade angular da barra , mas vamos supor que ela está girando no sentido anti-horário (sentido positivo):
E o vetor é:
Então, a velocidade do ponto será:
Resolvendo este produto vetorial, vamos ter que:
Então:
Passo 4
Agora sim temos duas equações que relacionam a velocidade do ponto :
E:
Vamos igualar estas equações:
Agora temos que separar as componentes e em duas equações:
Da segunda equação tiramos que:
E da primeira equação temos que:
Como a achamos um valor negativo, significa que arbitramos o sentido contrário para a velocidade angular da barra :
Passo 5
Nosso próximo passo é acharmos a aceleração angular da barra . Para isso, vamos usar a equação da aceleração do ponto com relação ao eixo móvel:
Vamos mais uma vez relacionar cada termo da equação com o que está acontecendo na situação do problema.
Como o ponto está fixo, ele não possui aceleração:
A aceleração angular da barra é:
A aceleração relativa corresponde a aceleração do ponto quando ele se move no eixo móvel. Como o colar só pode se mover ao longo da barra , o vetor aceleração será:
Não esqueça que tem que decompor o vetor velocidade relativa, cujo valor achamos no passo anterior, nos eixos também. Vai ficar assim:
E o restante dos termos nós já sabemos, então a nossa equação fica:
Vamos resolver cada um dos produtos vetoriais:
O próximo nós já tínhamos resolvido antes:
Então:
Calma, vamos para o nosso último produto vetorial:
Agora, vamos substituir isso na nossa equação lá de cima:
Beleza?
Vamos dar aquela ajeitada na nossa equação:
Bem melhor agora, né?
Mas ainda não conseguimos achar a aceleração angular da barra só com esta equação aí. Temos que partir para outra!!!
Passo 6
Vamos usar a barra para calcular a aceleração do ponto , já que ele realiza um movimento circular em torno do ponto que é fixo:
Sabemos que:
E que:
Nós não sabemos o valor deda aceleração angular da barra , mas vamos arbitrar o sentido positivo:
Então a nossa equação fica:
Resolvendo esse produto vetorial temos que:
Então:
Passo 7
Pronto! Agora temos duas equações que relacionam a aceleração do ponto :
E:
Vamos igualar essas equações:
Agora é só separar as componentes e cada qual na sua equação:
Da segunda equação tiramos que:
E da primeira equação temos que:
Como o sinal deu negativo, significa que arbitramos o sentido contrário para a aceleração angular da barra :