Trabalho e Energia
Teoria
Introdução
Imagine você empurrando seu carro enguiçado, fazendo aquela força...
Logo logo você estará beeem cansado, né?
Isso porque você está realizando trabalho. Calma, eu sei que dá trabalho empurrar um carro, mas não é desse trabalho que estamos falando aqui.
Trabalho é a quantidade de energia utilizada por uma força para deslocar um corpo por uma certa distância.
Vamos entender melhor isso aí, então!
Trabalho
Uma força realiza trabalho sobre um corpo quando este sofre um deslocamento na direção da força.
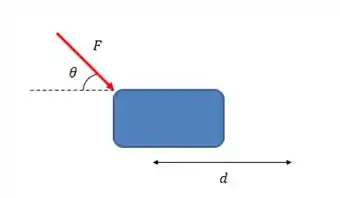
Matematicamente falando, trabalho, que vamos chamar de , é o deslocamento multiplicado pela componente da força na direção do deslocamento:
Por que usamos um cosseno? Porque precisamos usar a componente da força que atua na direção do deslocamento e apenas ela.
Agora imagina que o corpo tenha um deslocamento beeem pequeno, ou seja, um deslocamento infinitesimal , então vamos ter um trabalho infinitesimal também:
Não esqueça que:
- A componente , que é perpendicular à direção do deslocamento, não realiza trabalho;
- Trabalho é positivo quando a componente tem o mesmo sentido do deslocamento e é negativo se tem o sentido oposto;
- Trabalho é uma grandeza escalar, não um vetor e sua unidade é em Joule (J).
Agora vamos ver alguns casos de trabalho...
Trabalho da Força Variável
Se um corpo sofre um deslocamento variável ao longo de sua trajetória, vamos ter que integrar para achar o trabalho. Se tivermos um gráfico de uma força que varia em função do deslocamento, por exemplo:
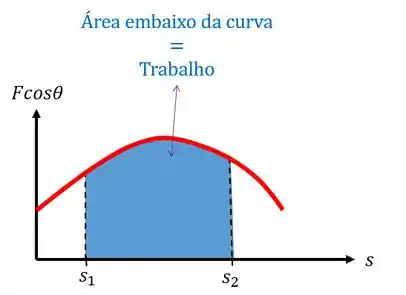
O trabalho será calculado integrando a equação dessa curva:
Essa �� a forma mais geral de se calcular o trabalho.
Trabalho de uma Força Constante
Imagine uma força constante atuando em um bloco enquanto ele se desloca de para :
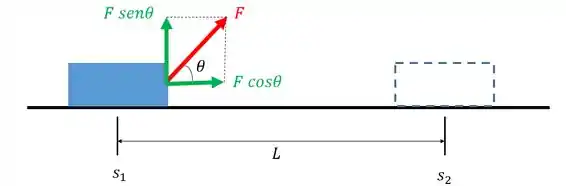
O trabalho U dessa força será:
Como ficaria essa força num gráfico?
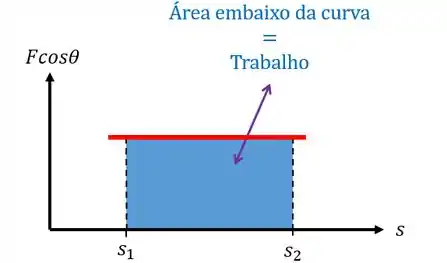
A força não é constante? Então, o gráfico fica uma reta constante e o trabalho vai ser igual a área embaixo da reta.
Trabalho da Força Peso
Imagine um corpo subindo na vertical...
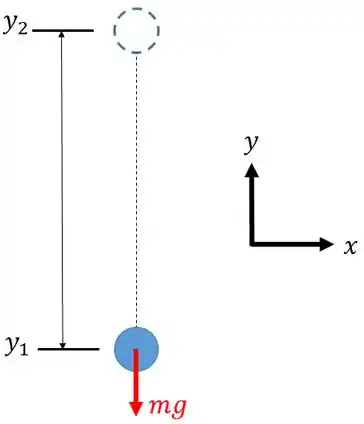
Apesar dele estar subindo, existe a força peso devido a presença da gravidade. Essa força vai realizar um trabalho assim:
Repare que a força aponta no sentido contrário ao movimento do corpo, logo o trabalho vai ser negativo.
Agora imagine um corpo caindo...
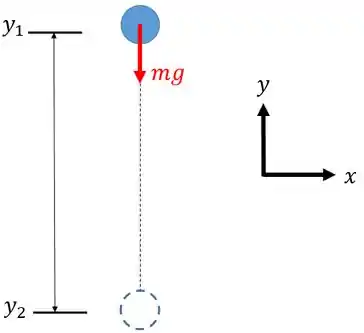
Ele está sob a ação da aceleração da gravidade de modo que a única força que vai estar atuando nele é o peso. Vamos integrar essa força:
Repare que o sinal negativo é porque a força peso aponta para o sentido negativo do eixo . Mas você pode se perguntar... Por que o trabalho está negativo se a força está apontando no mesmo sentido do deslocamento?
Observe que tem um valor menor do que , então quando fizermos a subtração de isso vai dar um valor negativo, o que vai anular o sinal de menos da força . Portanto, no fim das contas o trabalho é positivo!!!!
Trabalho da Força de uma Mola
Você lembra como se calcula a força de uma mola? É assim:
Onde, é a rigidez da mola e é o deslocamento.
Imagina que tenho uma mola em sua posição normal, sem nenhuma deformação e então aplico uma força puxando essa mola de modo que ela sai da posição inicial e chega na posição final :
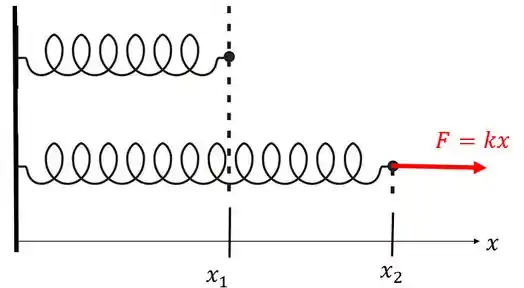
O trabalho realizado sobre a mola pela força é:
Repare que tanto quando você puxa uma mola quanto comprimi, a força vai estar no mesmo sentido do deslocamento.
E quando tem um corpo preso a uma mola... Qual será o trabalho que a mola faz no corpo?
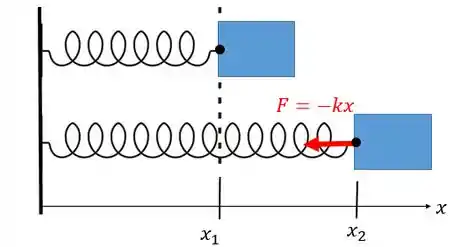
Repare que quando puxamos a mola, ela tende a voltar a sua posição inicial, certo? Então, o que o corpo vai sentir? Pela terceira lei de Newton de ação e reação, o bloquinho tenderá a ser puxado de volta pela mola, surgindo uma força:
Então, o trabalho feito pela mola no bloco será:
Repare que o trabalho é negativo, pois a força está em sentido contrário ao deslocamento.
Energia Cinética
Se um corpo de massa está em movimento com uma velocidade , existe uma energia associada a esse movimento dada por:
Essa é a chamada energia cinética que vamos chamar de .
Teorema Trabalho-Energia Cinética
Agora pense: Se você empurrar uma caixa, estará aplicando uma força nela, certo? Mas sabemos que se uma força provoca deslocamento, então há trabalho...
O que acontecerá com a energia cinética desta caixa?
Bem, suponha que a caixa estava em repouso no início e, após a realização do trabalho, passe a se movimentar com uma velocidade . Você conseguiu gerar uma variação de energia cinética nesse corpo, não é mesmo?
Assim:
Onde é a velocidade final e a velocidade inicial.
De certa forma, podemos dizer que você transferiu energia para a caixa. Mas lembra daquela ideia que a energia sempre se conserva?
Bom, por causa disso, podemos dizer que a energia que você transferiu tem que ser igual a energia ganha pela caixa. Sendo assim:
Sendo que a energia que você transferiu é igual ao trabalho realizado e a variação de energia cinética é igual à energia que a caixa ganhou.
E é esse o famoso teorema Trabalho-Energia cinética:
Vamos praticar com os exercícios? Partiu, então!!!
Não esqueça que:
Trabalho da Força Variável
Trabalho de uma Força Constante
Trabalho da Força Peso
Trabalho da Força de uma Mola
Energia Cinética
Teorema Trabalho-Energia Cinética
Exercícios Resolvidos
Exercício Resolvido #1
J.L. Meriam & L.G. Kraige, Mecânica para engenharia, Dinâmica, 6° ed. RJ: LTC, 2009, 120, 3/103
Utilize o método de trabalho-energia para desenvolver uma expressão para a altura máxima atingida por um projétil que é lançado com velocidade inicial a partir do nível do solo. Avalie sua expressão para . Assuma uma aceleração gravitacional constante e despreze a resistência do ar.
Passo 1
Temos que:
Onde é o estado da bolinha no solo ao ser lançada e o ponto de atura máxima, o qual estamos analisando.
Passo 2
Sabemos que:
Em 1:
Em 2:
Já que a bola se encontra parada no ponto de altura máxima.
Passo 3
O trabalho será dado por:
Negativo já que a força está indo contra ao movimento.
Assim:
Resposta
Exercício Resolvido #2
J.L. Meriam & L.G. Kraige, Mecânica para engenharia, Dinâmica, 6° ed. RJ: LTC, 2009, 121, 3/112
O vetor posição de uma partícula é dado por , onde é o tempo em segundos a partir do início do movimento e onde é expresso em metros. Para a condição em que , determine a potência desenvolvida pela força que age sobre a partícula.
Passo 1
Sabemos que:
Assim, para
Passo 2
Assim:
Resposta
Exercício Resolvido #3
J.L. Meriam & L.G. Kraige, Mecânica para engenharia, Dinâmica, 6° ed. RJ: LTC, 2009, 121, 3/108
O guindaste sobre esteiras equipado para demolição está se deslocando a uma velocidade constante de quando é subitamente parado. Calcule o ângulo máximo por meio do qual o cabo da bola de demolição oscila.
Passo 1
A bolinha está se deslocando com uma velocidade de Quando o guindaste parar, a bolinha irá subir:
A força que estará atuando nesse sistema e exercendo trabalho será a força peso, que será contrária ao movimento, ou seja, o seu trabalho será negativo.
Passo 2
Quanto vale a altura que a bolinha sobe em função de
Basta você perceber que se é igual ao lado adjacente do triângulo e que é o valor do comprimento total, a altura vai ser a diferença entre esses valores:
Assim:
Passo 3
Basta a gente aplicar o teorema trabalho energia agora:
No estado a bolinha está em repouso. Além disso o trabalho é negativo:
Vamos converter a velocidade para
Passo 4
Assim:
Assim:
Resposta
Exercício Resolvido #4
J.L. Meriam & L.G. Kraige, Mecânica para engenharia, Dinâmica, 6° ed. RJ: LTC, 2009, 121, 3/107
O cursos de parte do repouso em e desliza com atrito desprezível sobre a haste fixa no plano vertical. Determine a velocidade com que o cursor golpeia a extremidade quando atuado por uma força de , que possui uma direção constante. Despreze as pequenas dimensões do cursor.
Passo 1
Podemos representar o sistema pelo desenho abaixo:
Passo 2
Temos que:
Só que, o trabalho realizado entre será a soma dos trabalhos da força de e do peso.
Passo 3
Vamos analisar primeiro a força de , que é a mais difícil. Veja bem: Existe um componente em , que tem que ser multiplicada pela distância percorrida em de até , e uma componente em , que deve ser multiplicada pela distância percorrida em
Por que existe um sinal de negativo? Porque a componente em aponta na direção contrária ao deslocamento.
Beleza, agora vamos analisar o trabalho da força peso.
Passo 4
O trabalho do peso será positivo, já que o peso está agindo de forma a aumentar a velocidade do corpo:
Assim:
E as energias cinéticas? O corpo parte do repouso e atinge uma velocidade ao fim. Sendo assim, a variação de energia cinética será dada por:
Passo 5
Voltando ao início:
Então:
Resolvendo:
Resposta
Exercício Resolvido #5
J.L. Meriam & L.G. Kraige, Mecânica para engenharia, Dinâmica, 6° ed. RJ: LTC, 2009, 122, 3/117
A mulher de sobe o lance de escadas em segundos. Determine a potência média desenvolvida.
Passo 1
Como sabemos, a potência de uma força é dada por:
No caso não-diferencial.
Passo 2
Qual é a força atuando? O peso. Pra calcularmos o trabalho do peso, basta multiplicarmos o valor da força vezes o deslocamento na direção dessa força. No caso:
Assim:
Resposta
Exercício Resolvido #6
J.L. Meriam & L.G. Kraige, Mecânica para engenharia, Dinâmica, 6° ed. RJ: LTC, 2009, 122, 3/12
A resistência à penetração de um projétil de disparado com uma velocidade de em um bloco de material fibroso é apresentada no gráfico. Represente essa resistência pela linha tracejada e calcule a velocidade do projétil para o instante em que se o projétil é levado a parar após uma penetração total de .
Passo 1
Para achar vamos usar:
Passo 2
Para um deslocamento de
O que fizemos? Fizemos uma regra de três para achar a reação para a situação em que
Agora:
Resposta
Exercício Resolvido #7
J.L. Meriam & L.G. Kraige, Mecânica para engenharia, Dinâmica, 6° ed. RJ: LTC, 2009, 122, 3/115
No projeto de um sistema de esteiras transportadoras, pequenos blocos metálicos são descarregados com uma velocidade de sobre uma rampa pela esteira transportadora superior mostrada. Se o coeficiente de atrito dinâmico entre os blocos e a rampa é de , calcule o ângulo Ѳ que a rampa deve fazer com a horizontal para que os blocos sejam transferidos sem deslizar para a esteira transportadora inferior que se move na velocidade de .
Passo 1
O sistema pode ser representado por:
E a distância na direção Basta a gente aplicar:
Passo 2
A força resultante aplicada no corpo será dada por:
Assim, o trabalho será dado por:
Passo 3
A variação da energia cinética será dada por:
Assim, aplicando o teorema trabalho-Energia :
Resolvendo: