Mancais
Teoria
Introdução
Você sabe o que é um Mancal?
Mancais são estruturas que servem de apoio para eixos giratórios.
Nesse tópico vamos aprender um pouco sobre a Física desses elementos. Bora lá!
Mancais Radiais
Mancais radiais são aqueles que dão suporte lateral a um eixo. Basicamente, um eixo entra em um mancal radial e é separado da superfície do mancal por uma certa folga:
No desenho, o círculo mais interno representa o eixo e o mais externo a superfície do mancal.
Bom, agora imagine que o mancal esteja submetido a uma carga axial Para o corpo ser equilibrado, surgirá uma reação da superfície para o mancal, de mesmo módulo que mas de sentido contrário:
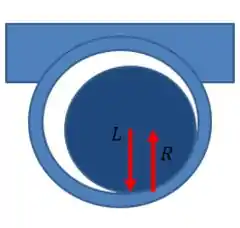
No entanto, essas duas forças não vão ser colineares, ou seja, não estão alinhadas. Pelo contrário, a força será aplicada a uma distância do centro do eixo, numa região conhecida como círculo de atrito:
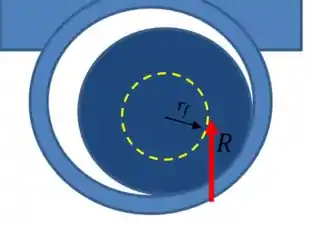
Sendo assim, a reação vai gerar um momento dado por:
Como:
E Esse carinha é dado por:
Onde é o ângulo de atrito.
Beleza, e se quisermos girar o eixo? Qual o momento necessário para que isso ocorra?
O momento necessário será exatamente
E é isso. Na maioria das questões você terá que usar essa equação do momento! Vamos ver isso melhor nos exercícios.
Mancais de Escoras e Atrito entre Discos
Nesse tipo de mancal, geralmente existem duas superfícies que são comprimidas uma contra a outra, o que gera um atrito entre elas:
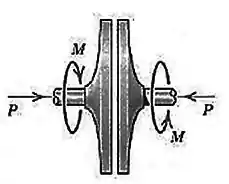
Surge, então, da mesma forma que no outro tipo de mancal, a mesma pergunta: Qual é o momento necessário para fazer o mancal girar?
O momento, nesse caso, é dado pela integral:
Onde:
- : o coeficiente de atrito entre os discos;
- a pressão de contato entre os discos;
- a distância do termo infinitesimal até o centro do disco;
- o elemento infinitesimal de Área.
Sendo que essa área onde estamos integrando é a área de contato entre as duas superfícies. Se forem dois círculos, sendo um menor que o outro, será a área do círculo menor.
Quando a pressão for constante:
Para um caso em que a pressão de contato entre as placas é constante, podemos dizer que:
Assim:
Substituindo na integral:
Chamando de:
Assim:
Essa é a equação para o caso em que a pressão é constante! Guarde-a na memória.
E se o mancal que aparecer tiver o formato de um anel com raio interno () e raio externo (), você vai ter que utilizar esta fórmula aqui:
Bora praticar agora!!!
Mancais de Escoras e Atrito entre Discos
Exercícios Resolvidos
Exercício Resolvido #1
J.L. Meriam & L.G. Kraige, Mecânica para engenharia, Estática, 6° ed. RJ: LTC, 2009, 270, 6/71
Os dois rotores estão montados no mesmo eixo, que está apoiado por um mancal radial entre eles. Cada rotor tem uma massa de e o diâmetro do eixo vale Se um momento de é necessário para manter a rotação dos rotores e do eixo em uma velocidade constante baixa, calcule:
- O coeficiente de atrito no mancal.
- O raio do círculo de atrito.
Passo 1
No caso de um mancal radial, podemos relacionar a carga radial , o raio do eixo , o seno do ângulo de atrito () e o momento com a seguinte fórmula:
Quem é a carga radial nesse caso? É o próprio peso dos rotores!
Então, vamos calcular este peso:
Multiplicamos o peso por , pois temos rotores!
Passo 2
O raio do eixo vale:
Agora podemos calcular o ângulo de atrito sabendo que o momento necessário para manter a rotação dos rotores e do eixo é de , então:
Assim, o ângulo de atrito será:
Sabendo o ângulo de atrito podemos calcular o coeficiente de atrito , pois:
Então, podemos calcular da seguinte forma:
Passo 3
E para calcular o raio do círculo de atrito? Basta a gente usar:
Resposta
Exercício Resolvido #2
J.L. Meriam & L.G. Kraige, Mecânica para engenharia, Estática, 6° ed. RJ: LTC, 2009, 270, 6/73
O disco circular é colocado sobre o topo do disco e submetido a uma força compressiva de . Os diâmetros de e valem e, respectivamente, e a pressão em cada disco é constante em toda a superfície. Se o coeficiente de atrito entre e vale , determine o momento que fará com que deslize sobre . Além disso, qual é o coeficiente de atrito mínimo entre e a superfície de apoio que impedirá que gire?
Passo 1
Para calcular o momento temos que usar a nossa fórmula aqui:
Onde é o raio do círculo menor, pois o disco é que vai girar. E é a força compressiva de .
Passo 2
Para o primeiro caso, estamos considerando o momento que fará com que deslize sobre . Basicamente, estaremos calculando o momento máximo que causa a iminência do movimento.
Sendo assim, o raio que vamos usar é o raio do círculo menor:
Então, o momento será:
Passo 3
Agora queremos saber qual o coeficiente de atrito mínimo que impede o giro da placa sobre
O que continua constante nos dois casos? O momento!!!
Como um momento de está sendo aplicado na placa , a placa precisará aplicar um momento contrário, mas de mesmo módulo, para impedir a rotação. Sendo assim:
Ah, e agora o raio será o raio de
Então, o momento será calculado pela nossa fórmula:
Resposta
Exercício Resolvido #3
J.L. Meriam & L.G. Kraige, Mecânica para engenharia, Estática, 6° ed. RJ: LTC, 2012, 270, 6/74
Determine a força trativa no cabo para suspender a carga de se o coeficiente de atrito para o mancal de vale . Determine, também, a força trativa na seção estacionária do cabo. As massas do cabo e da polia são pequenas e podem ser desprezadas.
Passo 1
Podemos desenhar nosso sistema assim:
O é calculado assim:
Mas antes temos que calcular o ângulo :
Então, será igual a:
Passo 2
Para determinar as forças, temos que usar as equações de equilíbrio.
Vamos começar fazendo o somatório de momentos com relação ao ponto , considerando o momento positivo girando no sentido anti-horário:
Passo 3
Agora vamos fazer o equilíbrio das forças verticais:
Vamos substituir nesta equação que acabamos de achar:
E vai ser:
Resposta
Exercício Resolvido #4
J.L. Meriam & L.G. Kraige, Mecânica para engenharia, Estática, 6° ed. RJ: LTC, 2009, 270, 6/76
Calcule o torque necessário para girar o carretel de cabo telefônico de no sentido horário contra a força trativa de no cabo. O diâmetro do mancal vale e o coeficiente de atrito para o mancal é
Passo 1
Vamos lembrar um conceito que vimos em tópicos anteriores: o conceito de sistema força binário resultante.
Queremos calcular o momento necessário para fazer o carretel girar no sentido horário, certo? Mas antes disso, temos que calcular os momentos contrários a esse movimento.
O momento da força de em relação ao ponto no centro do carretel é dado por:
Isso no sentido anti-horário.
Passo 2
Agora vamos representar o sistema de forças completo:
A força peso do carretel tem módulo de:
Tá vendo? Deslocamos a força de para o ponto que queremos, além de representar o seu momento por meio de um binário. Que ponto é esse? É o ponto localizado a uma distância do centro do sistema.
Agora devemos calcular a força resultante devido à força aplicada e ao peso.
Assim:
Assim, o módulo dessa força vale:
Passo 3
Agora vamos descobrir o ângulo de atrito:
Com isso vamos poder calcular . É importante calcular porque a força resultante vai estar localizada a essa distância do centro do círculo. Repare que no enunciado foi dado o diâmetro do mancal que vale , mas temos que usar o raio do mancal para calcular :
Com isso, podemos calcular o momento gerado pela força resultante:
Passo 4
Show de bola! Já temos tudo que precisamos para calcular o momento . Esse momento tem que se opor aos dois momentos que calculamos antes de forma a fazer com que o sistema fique na iminência de girar. Assim:
Resposta
Exercício Resolvido #5
J.L. Meriam & L.G. Kraige, Mecânica para engenharia, Estática, 6° ed. RJ: LTC, 2012, 271, 6/79
O peso do tambor e de seu cabo é de e o coeficiente de atrito para o mancal vale . Determine a força necessária para suspender o cilindro de se o atrito no mancal é desprezível e incluído na análise. O peso do eixo é desprezível.
Passo 1
Para o primeiro caso em que o atrito é zero, vamos ter que:
Então, podemos desenhar nosso sistema assim:
Repare que levamos a força para o ponto central do tambor, mas para fazer isso temos que levar o momento que esta força faz com relação a este ponto:
Beleza?
Passo 2
Para achar o valor da força é só fazermos o somatório de momentos com relação ao ponto :
Passo 3
Agora vamos considerar o atrito, então:
Então, precisamos calcular o ângulo :
Portanto, será:
Passo 4
Para esta nova situação, podemos desenhar o nosso sistema assim:
Para achar o valor da força vamos fazer o somatório de momentos com relação ao ponto :
Resposta
Exercício Resolvido #6
J.L. Meriam & L.G. Kraige, Mecânica para engenharia, Estática, 6° ed. RJ: LTC, 2012, 272, 6/87
Cada uma das quatro rodas do veículo tem uma massa de e está montada em um eixo de de diâmetro. A massa total do veículo é , incluindo as rodas, e está distribuída igualmente pelas quatro rodas. Se uma força é necessária para manter o veículo rodando sob uma velocidade constante baixa sobre uma superfície horizontal, calcule o coeficiente de atrito que existe nos mancais das rodas. (Sugestão: Desenhe um diagrama de corpo livre completo para uma roda.)
Passo 1
Como foi sugerido, vamos montar o nosso diagrama de corpo livre para uma das rodas:
O peso do veículo () suportado por cada roda vai ser o peso total dividido entre as quatro rodas. Mas repare que a massa de também inclui a massa das quatro rodas.
Então, a massa do veículo () vai ser:
Com isso, o peso do veículo fica:
E o peso de cada roda () será:
Repare também a força foi dividida entre as quatro rodas e por isso ficamos com:
Beleza?
Passo 2
Fazendo o equilíbrio de forças verticais na roda, surge uma força normal igual a:
E fazendo o equilíbrio das forças horizontais, temos:
Então, vamos ter o seguinte diagrama de corpo livre:
Repare que se fizermos o somatório de momentos com relação ao ponto , surge um momento devido a força .
Então, para termos um equilíbrio precisa surgir um momento :
Passo 3
Sabendo que o momento em um mancal é calculado por:
Onde, é a carga suportada pelo mancal que vai ser o peso do veículo:
E é o raio do mancal que vale:
Então, vamos ter que:
Agora sim podemos calcular o coeficiente de atrito:
Resposta
Exercício Resolvido #7
J.L. Meriam & L.G. Kraige, Mecânica para engenharia, Estática, 6° ed. RJ: LTC, 2012, 272, 6/89
O caixote de é abaixado para uma câmara de armazenamento subterrânea em um elevador de dois parafusos projetado como mostrado. Cada parafuso tem uma massa de , um diâmetro médio de e uma rosca quadrada simples com um passo de . Os parafusos são girados em sincronismo por uma unidade motorizada na base do dispositivo. Toda a massa do caixote, dos parafusos e da plataforma de do elevador é sustentada uniformemente por mancais radiais planos em , cada um tendo um diâmetro externo de e um diâmetro interno de . A pressão nos mancais é considerada uniforme sobre toda a superfície dos mancais. Se o coeficiente de atrito para os mancais radiais e os parafusos em vale , calcule o torque que deve ser aplicado a cada parafuso para suspender o elevador e para abaixar o elevador.
Passo 1
Para suspender o elevador, é necessário apertar os parafusos, então vamos usar a seguinte equação:
Então, vamos começar calculando o ângulo de hélice ():
O passo do parafuso () vale 11 e o raio vai ser a metade do diâmetro que foi dado no enunciado:
Então, o ângulo de hélice () será:
Passo 2
Sabendo que o coeficiente de atrito () vale , vamos ter que o ângulo de atrito () será:
Passo 3
A carga axial vai o peso do caixote somado com o peso da plataforma:
Repare que a unidade de massa foi dada em () e é preciso passar para () para calcular o peso!
Então, o momento necessário para apertar cada parafuso será:
Repare que a carga axial foi dividida pela metade já que cada parafuso suporta metade do peso total!
Passo 4
E para abaixar o elevador precisamos afrouxar o parafuso, então vamos ter que:
Passo 5
Agora vamos calcular o momento devido ao atrito nos mancais...
Repare que foi dito no enunciado que a pressão nos mancais é uniforme. Mas pela figura que mostra o mancal, vemos que ele tem o formato de um anel, ou seja, possui um raio interno () e um raio externo .
Nesse caso, temos que usar a seguinte equação:
A força vai ser o peso total do sistema:
Então, para cada mancal vamos ter que:
Passo 6
Então, para suspender o elevador o momento total será:
E para abaixar o elevador vamos ter que o momento total vai ser de:
Resposta
Exercício Resolvido #8
J.L. Meriam & L.G. Kraige, Mecânica para engenharia, Estática, 6° ed. RJ: LTC, 2009, 273, 6/91
Determine a expressão para o torque necessário para girar o eixo cuja pressão axial é sustentada por um mancal cônico. O coeficiente de atrito é e a pressão no mancal é constante.
Passo 1
Opa! Esse mancal aí é diferente, né?
Mas vamos dar um jeito resolver esse problema, fique tranquilo!
A pressão nesse caso também não é constante, já que a seção transversal é variável. No caso constante, nós usamos:
Nesse caso, vamos usar:
Passo 2
A área que queremos integrar é definida pelos limites e
Mas quem é
Geralmente escrevemos algo como:
Mas no nosso caso, a nossa dimensão está curvada, já que a superfície é inclinada. Veja no triângulo abaixo:
Desse modo, podemos escrever:
Assim:
Vamos agora escrever em função de . Observe o nosso triângulo:
Perceba que:
Então, substituindo na nossa equação de temos que:
Passo 3
Perceba também que a pressão faz um ângulo com a horizontal. Nós estamos integrando para achar , que é totalmente vertical. Por isso que estamos integrando que é a componente vertical de e é dada por:
Ufa! Jogando tudo na integral:
Arrumando isso aí, temos que:
Passo 4
Vamos integrar em Mas quais são os limites de integração?
Usando dois triângulos marotos, vamos usar a trigonometria para achar esses limites, que são coordenadas de
Assim:
E:
Assim:
Agora já podemos integrar:
Mas já achamos os valores de e , então vamos substituí-los:
Simplificando isso aí, vamos ter que:
Como o que precisamos saber é a pressão , vamos isolá-la:
Pronto! Vamos agora falar do momento.
Passo 5
O momento é dado por:
A boa notícia é que já definimos e. Então, basta a gente tacar tudo ali naquela integral:
Arrumando essa bagunça:
Agora é só substituir os limites:
Vamos cortar as tangentes ao cubo com a tangente ao quadrado:
Lembrando que , podemos escrever a nossa equação assim:
Então, cortando os cossenos, vai nos restar:
Ufa! Agora é só substituir o valor que encontramos para pressão em função de nesta equação do momento aí de cima:
Assim: