Cunhas e Parafusos
Produzido por Pablo RicardoTeoria
Introdução
Você sabe o que é uma cunha?

Uma cunha é uma espécie de apoio. Usamos isso para apoiar máquinas, ferramentas, mesas e corpos no geral.
Nesse capítulo, vamos aprender um pouco da Física que faz com que essas ferramentas sejam tão úteis!
Além disso, vamos falar um pouco sobre parafusos:

Precisamos estudar parafusos? Sim, parafusos são mecanismos bastante sofisticados.
Partiu?
O ângulo de atrito
Imagine uma caixa em cima de uma superfície que possui atrito. Ela sofrerá a ação de uma força de atrito, certo?
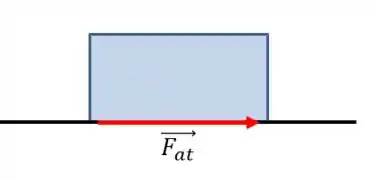
Mas ela também sofre a ação de uma força normal, certo?
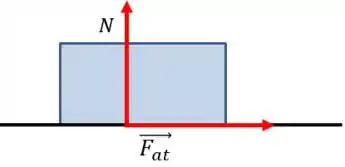
Podemos, então, representar o efeito das duas forças por meio de uma resultante
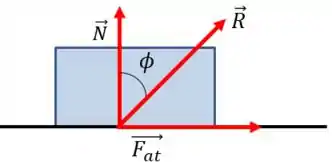
Perceba que essa resultante faz um ângulo com a direção da força normal. Mas qual é o valor deste ângulo? É só considerarmos esse triângulo retângulo aqui:
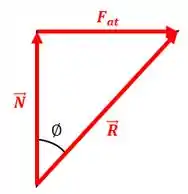
A força de atrito pode ser calculada assim:
Onde pode ser o coeficiente de atrito estático ou dinâmico, dependendo da situação!
Então, podemos dizer que:
Então, o nosso ângulo de atrito será igual a:
Vamos usar essa relação muitas vezes nesse e nos próximos tópicos de atrito!
Observação: O ângulo é definido sempre entre a direção normal à superfície que possui atrito e a força resultante naquela superfície.
Cunhas
Imaginemos uma cunha que sustenta um corpo, como no desenho abaixo:
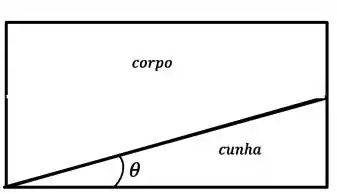
O atrito da superfície do corpo com a cunha e da cunha com o chão é o mesmo e tem coeficiente , beleza?
Assim, existem duas reações que afetam a cunha: , que é a resultante (também chamada de reação) do chão com a cunha, e , que é a reação do corpo com a cunha:
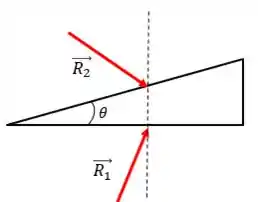
Mas você deve ter percebido que esse sistema não está equilibrado, certo? Certo! Vamos precisar aplicar uma força pra equilibrar:
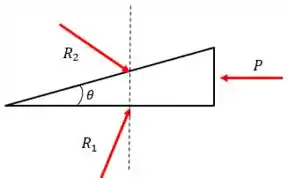
Como dimensionamos Essa é uma pergunta frequente dos problemas! ![]()
Bom, vamos precisar usar as equações de equilíbrio de forças:
E para fazer o equilíbrio, precisamos achar as componentes vertical e horizontal das reações. Então, precisamos descobrir os ângulos das forças.
faz um ângulo com a normal e também. Porém, como a superfície de é inclinada, devemos contabilizar essa inclinação na conta:
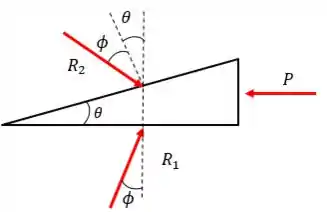
E como nós fizemos aparecer aquele á em cima? Vamos dar uma olhadinha na geometria da coisa.
Primeiro, observe que o ângulo abaixo, , surgiu porque a soma dos ângulos internos de um triângulo deve ser :
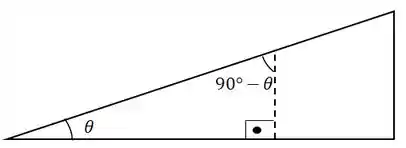
Beleza, agora vamos traçar uma perpendicular à superfície do plano inclinado da cunha:
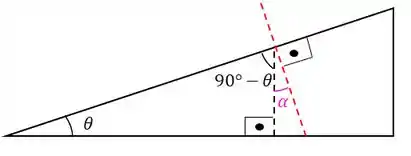
A linha vermelha representa a reta normal. Tá vendo aquele ângulo ali? Podemos calculá-lo assim:
Beleza?
Agora vamos apagar esses ângulos:
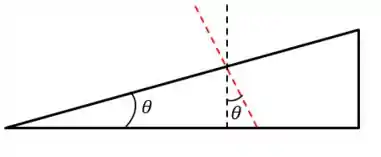
Lembra que ângulos opostos por um vértice são iguais? Assim:
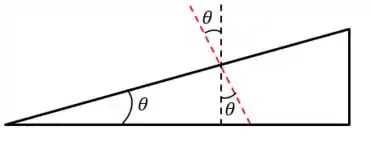
Pronto, agora entendemos o aparecimento do !
E o ? O ângulo de atrito é sempre tomado em relação à normal da superfície. Assim:
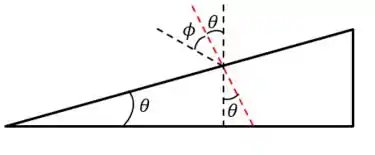
Pronto! Com isso vamos conseguir calcular Vamos ver isso melhor nos exercícios, não se preocupe.
Cunha auto-travante:
Vimos que existe uma força que equilibra o sistema. Mas será que existe alguma condição que faz com que a cunha não deslize, mesmo sem a ação de uma força
Sim, essa condição é:
Além disso, temos um limiar do deslizamento, dado por:
Parafusos
As questões de parafusos não exigem, geralmente, uma grande visualização geométrica. Em outras palavras, você vai precisar apenas saber usar as fórmulas e compreender quando usá-las.
Sendo assim, não vamos perder muito tempo com demonstrações de fórmulas. Vamos logo para a aplicação:
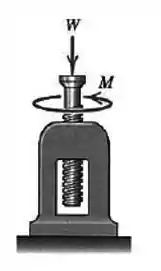
As variáveis que precisamos conhecer são:
- Carga axial que atinge o parafuso. Ex: o peso de um corpo.
- Raio do Parafuso
- Passo do parafuso. O passo nada mais é do que a distância que o parafuso percorre em uma volta.
- Ângulo de atrito. Como vimos antes:
- Ângulo de Hélice. É dado por:
- O momento para parafusar ou desparafusar o parafuso. Geralmente é o que queremos calcular.
Para ficar mais claro: Quando a gente enrosca um parafuso, ele se desloca unidades de comprimento. Esse comprimento pode ser visualizado como a distância entre duas “voltas” da hélice do parafuso:

Para entender melhor o conceito de ângulo de hélice, você precisaria “desenrolar” um parafuso:

E construir o triângulo abaixo:
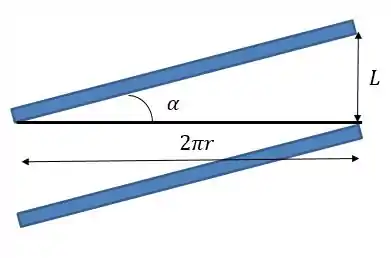
Perceba que o comprimento da base do triângulo vale , porque “desenrolamos” o parafuso.
Assim, podemos definir o ângulo como:
Geralmente o enunciado vai te dar as dimensões e e com elas você vai conseguir calcular esse ângulo.
Parafusando o Parafuso
Quando a questão nos pedir o momento necessário para parafusar um parafuso, ou seja, para pressioná-lo, devemos usar a seguinte fórmula:
Simples assim!
Desparafusando o Parafuso
Temos três casos:
- O parafuso foi corretamente parafusado e é auto-travante (não se desparafusa sozinho);
- O parafuso está no limiar do desparafusamento;
- O parafuso se desparafusa sozinho.
- O parafuso é auto-travante.
- O parafuso está no limiar do desparafusamento.
- O parafuso se desparafusa sozinho.
Esse caso ocorre sempre que Nessa situação, um momento , gerado pela estrutura no parafuso, impede o seu desparafusamento. Mas e se você quiser desparafusá-lo? Bom, aí você precisa aplicar um momento dado pela fórmula abaixo:
Nesse caso o parafuso não está ainda solto, mas sim no limiar do desparafusamento. Geralmente essa condição é usada para se calcular o coeficiente de atrito mínimo para que o parafuso não se solte.
A condição do limiar é dada sempre que os ângulos forem iguais:
Essa condição sempre ocorre quando
Nesse caso, o parafuso não foi corretamente pressionado e se desparafusa sozinho. Mas e se você quiser impedir que isso aconteça?
Bom, aí você precisa aplicar um momento dado por:
Beleza! Chegamos ao fim...

Vamos treinar um pouco agora! Partiu?
Cunhas
Parafusos
Parafusando o Parafuso
Desparafusando o Parafuso
Exercícios Resolvidos
Exercício Resolvido #1
J.L. Meriam & L.G. Kraige, Mecânica para engenharia, Estática, 6° ed. RJ: LTC, 2009, 265, 6/52
Os elementos de um tubo de desodorante em barra são mostrados na figura. Para subir a barra de desodorante o disco é girado. O eixo rosqueado se conecta as roscas de base móvel o eixo não tem roscas no suporte fixo . A rosca quadrada dupla de de diâmetro tem um passo de Determine o coeficiente de atrito estático , para o qual o desodorante não descerá sob a ação da força . Despreze o atrito em
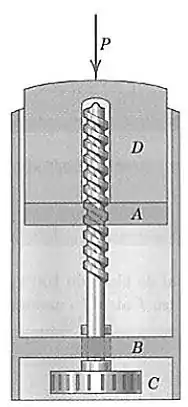
Passo 1
Queremos saber o coeficiente de atrito mínimo para que o parafuso não se solte. Nesse caso, o parafuso não está ainda solto, mas sim no limiar do desparafusamento.
Então, basta a gente lembrar que na condição limite do desparafusamento:
Onde:
E é:
Passo 2
Sabemos que:
A rosca tem um diâmetro de , então o seu raio é de . E o passo foi dito no enunciado que é de . Sendo assim:
Resposta
Exercício Resolvido #2
J.L. Meriam & L.G. Kraige, Mecânica para engenharia, Estática, 6° ed. RJ: LTC, 2009, 265, 6/56
O grampo está sendo usado para prender dois painéis enquanto a cola entre eles cura. Que torque deve ser aplicado à manopla do parafuso para produzir uma compressão de entre os painéis? O parafuso de rosca simples tem rosca quadrada com de diâmetro e passo (avanço por revolução) de O coeficiente de atrito efetivo vale Despreze qualquer atrito no pivô de contato em Que torque é necessário para afrouxar o grampo?
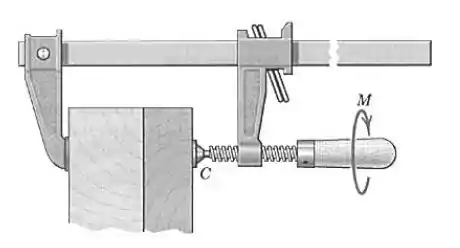
Passo 1
Nessa questão vamos aplicar as duas formulinhas que vimos. A primeira é fórmula do momento necessário para parafusar um parafuso que é:
E a segunda é a fórmula do momento necessário para desparafusar um parafuso:
Antes temos que calcular os ângulos que usaremos. Sabendo que o diâmetro é , então o raio será de e o passo é :
Sendo esse o ângulo de hélice.
E o ângulo de atrito é:
Passo 2
Lembrando que temos que passar tudo para metros para calcular o momento:
O momento para aparafusar será dado por:
Onde é a carga que o parafuso vai transmitir que é de , então:
Passo 3
E para desparafusar ou afrouxar? Basta usar a fórmula:
Resposta
Exercício Resolvido #3
J.L. Meriam & L.G. Kraige, Mecânica para engenharia, Estática, 6° ed. RJ: LTC, 2009, 265, 6/57
Especifique o torque necessário no parafuso motorizado para vencer a resistência de ao movimento do carro ao longo do seu trilho horizontal. O parafuso tem diâmetro médio de e tem duas roscas quadradas separadas que movem o carro por revolução do parafuso. O coeficiente de atrito vale .
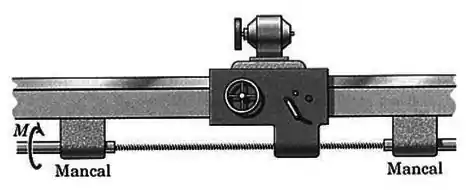
Passo 1
Para calcular o momento necessário para o parafuso vencer a resistência, temos que usar a seguinte fórmula:
Então, vamos começar calculando o ângulo de hélice ():
O passo do parafuso () nada mais é do que a distância que o parafuso percorre em uma volta, então vale . E o raio vai ser a metade do diâmetro que foi dado no enunciado:
Então, o ângulo de hélice () será:
Passo 2
Sabendo que o coeficiente de atrito () vale , vamos ter que o ângulo de atrito () será:
Passo 3
Sabendo que o parafuso precisa vencer uma carga de , então o momento necessário será:
Resposta
Exercício Resolvido #4
J.L. Meriam & L.G. Kraige, Mecânica para engenharia, Estática, 6° ed. RJ: LTC, 2009, 266, 6/60
O tensionador sustenta uma força trativa de no cabo. Os parafusos têm um diâmetro médio de e roscas quadradas com passo de . O coeficiente de atrito para as roscas lubrificadas não ultrapassa . Determine o momento aplicado ao corpo do tensionador para apertá-lo e para afrouxá-lo. Ambos os parafusos têm roscas simples e são impedidos de girar.

Passo 1
Para calcular o momento necessário para apertar o parafuso, temos que usar a seguinte fórmula:
Então, vamos começar calculando o ângulo de hélice ():
O passo do parafuso () vale e o raio vai ser a metade do diâmetro que foi dado no enunciado:
Então, o ângulo de hélice () será:
Passo 2
Sabendo que o coeficiente de atrito () vale , vamos ter que o ângulo de atrito () será:
Passo 3
Sabendo que existem dois parafusos e a carga axial () que atinge o parafuso é de , podemos calcular o momento necessário para apertar o tensionador:
Passo 4
Vamos calcular o momento para afrouxar o tensionador:
Resposta
Exercício Resolvido #5
J.L. Meriam & L.G. Kraige, Mecânica para engenharia, Estática, 6° ed. RJ: LTC, 2009, 266, 6/62
O anel está firmemente ajustado ao eixo e deve ser removido do eixo pelo dispositivo de remoção mostrado. O parafuso tem uma rosca quadrada simples com um diâmetro médio de e um passo de . Se um torque de é necessário para girar a roda de forma a retirar o anel do eixo, determine a pressão média (tensão compressiva) entre o anel e o eixo. O coeficiente de atrito para o parafuso em vale e o do eixo e do anel vale . O atrito na extremidade esférica do eixo pode ser desprezado.
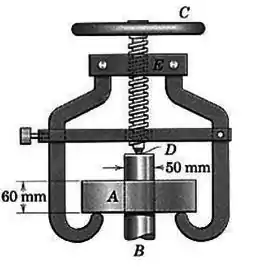
Passo 1
Para calcular o momento necessário para apertar o parafuso, temos que usar a seguinte fórmula:
Então, vamos começar calculando o ângulo de hélice ():
O passo do parafuso () vale e o raio vai ser a metade do diâmetro que foi dado no enunciado:
Então, o ângulo de hélice () será:
Passo 2
Sabendo que o coeficiente de atrito () vale , vamos ter que o ângulo de atrito () será:
Passo 3
Neste caso nós sabemos que o momento vale e queremos saber a força axial , então vamos ter que:
Passo 4
Agora precisamos saber a pressão . Para isso, temos que saber que a pressão é calculada por:
Onde, o coeficiente de atrito do eixo e do anel é e é a área de contato entre o anel e o eixo:
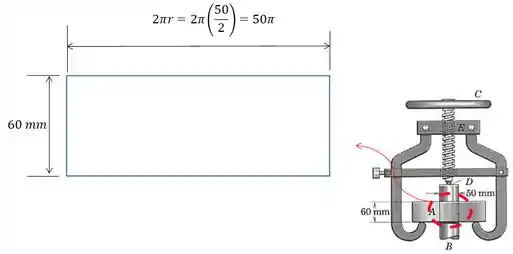
Então, a pressão será:
Resposta
Exercício Resolvido #6
J.L. Meriam & L.G. Kraige, Mecânica para engenharia, Estática, 6° ed. RJ: LTC, 2009, 265, 6/51
Se o coeficiente de atrito entre a cunha de aço e as fibras úmidas de um tronco recentemente cortado vale , determine o ângulo máximo que a cunha pode ter para não pular fora da madeira após ter sido atingida pela marreta.
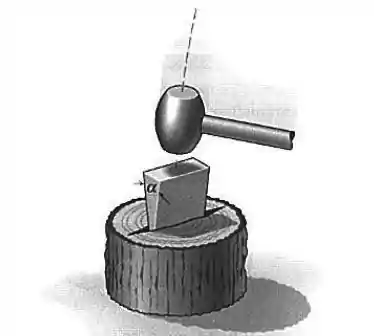
Passo 1
O sistema pode ser descrito assim:
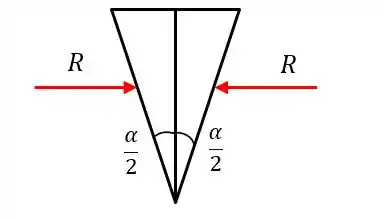
Para que a cunha seja auto-travante, devemos ter:
No caso limite, teremos:
Assim:
Resposta
Exercício Resolvido #7
J.L. Meriam & L.G. Kraige, Mecânica para engenharia, Estática, 6° ed. RJ: LTC, 2009, 265, 6/54
A porta industrial de e centro de massa em está sendo posicionada para reparo por meio da inserção de uma cunha de sob o canto . O movimento horizontal é impedido pelo pequeno degrau no canto Se os coeficientes de atrito estático nas superfícies superior e inferior da cunha valem , determine a força necessária para levantar a porta em
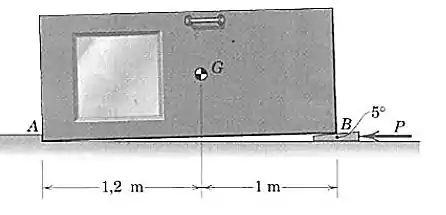
Passo 1
Vamos primeiro desenhar o sistema de forças na cunha:
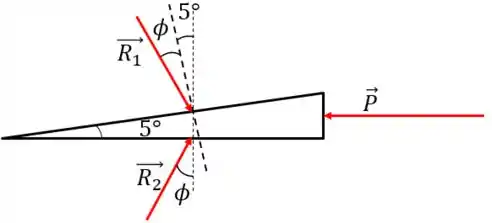
Vamos seguir uma estratégia: primeiro encontrar , depois vamos passar um eixo especial e decompor a força e nessa direção, achando, assim, o valor de
Passo 2
Vamos expandir um pouco o desenho de modo que possamos ver um pedaço da porta:
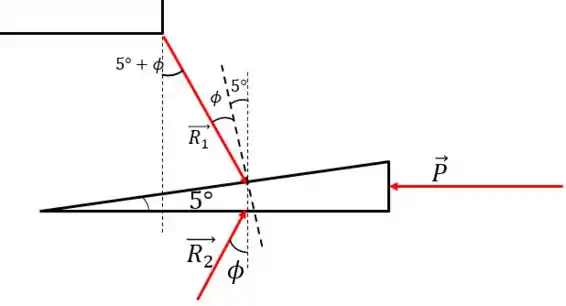
Perceba que o ângulo que a força faz com a aresta da porta é:
Mas quanto vale Este é o ângulo de atrito, sendo assim:
Agora vamos desenhar a nossa porta e as forças que atua nela:
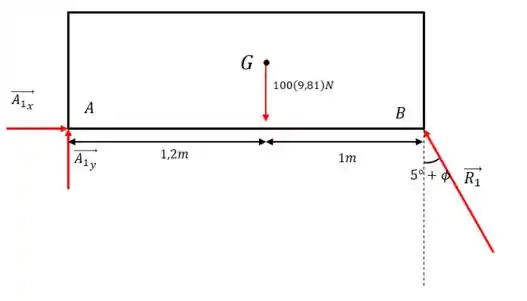
Como a porta exerce uma força na cunha, a cunha exerce a mesma força na caixa, certo?
Então, vamos usar o equilíbrio de momentos com relação ao ponto para calcularmos o valor de Fazer o momento com relação a este ponto nos ajuda porque assim eliminamos as forças em
Vamos achar as componentes da força :
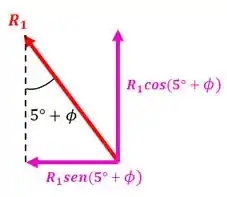
Perceba que o braço de alavanca com relação ao ponto é:
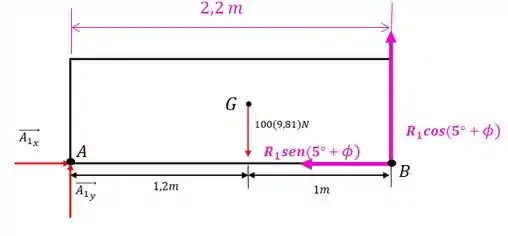
Pronto, agora podemos fazer o somatório de momentos com relação ao ponto :
Então, o valor de é:
Passo 3
Vamos traçar um eixo especial, perpendicular à linha de ação de e marcar os ângulos:
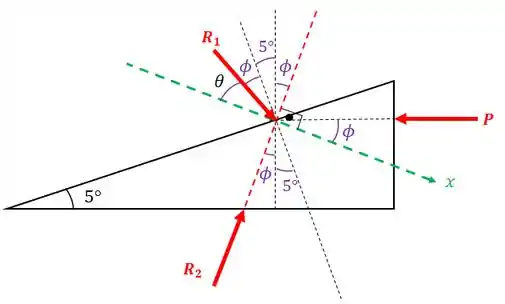
Vamos marcar melhor os ângulos:
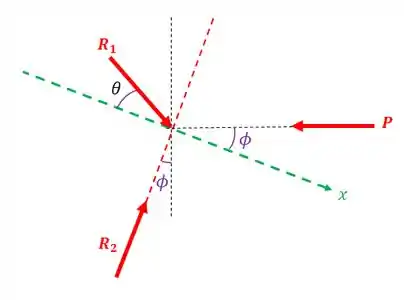
O ângulo entre e o eixo é , pois existe um ângulo de entre esse ângulo e o outro ângulo (que é aquele faz com a vertical)!!!
E
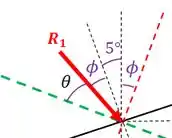
Olhando esse grupamento de ângulos, percebemos que a soma dos mesmos tem que dar . Assim:
Lembrando que :
Passo 4
Agora basta a gente fazer o equilíbrio das forças nesse eixo que criamos. Mas para isso temos que decompor as forças neste eixo:
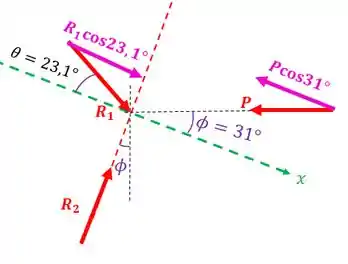
Resposta
Exercício Resolvido #8
J.L. Meriam & L.G. Kraige, Mecânica para engenharia, Estática, 6° ed. RJ: LTC, 2009, 266, 6/58
O coeficiente de atrito estático , entre o corpo de e a cunha com ângulo de vale Determine o módulo da força necessária para levantar o corpo de se:
- Rolamentos com atrito desprezível estejam colocados sob a cunha como mostrado.
- Os rolamentos sejam removidos e o coeficiente de atrito estático seja válido para essa superfície também.
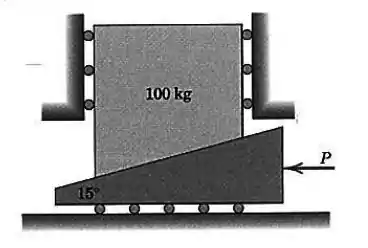
Passo 1
A presença dos rolamentos indica que não existe atrito na parte inferior da cunha.
Podemos, então, desenhar o sistema de forças na cunha como sendo esse:
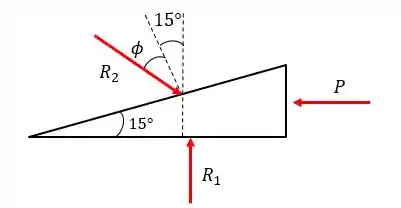
Perceba que a resultante é perpendicular e não inclinada neste caso, pois não existe atrito na parte de baixo da cunha.
Então, o ângulo de atrito é:
Olhando para o equilíbrio horizontal desse sistema, podemos achar uma relação entre e .
Mas antes temos que achar a componente horizontal da força :
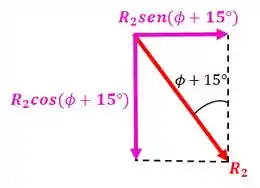
Então:
Passo 2
Agora vamos olhar para o corpo:
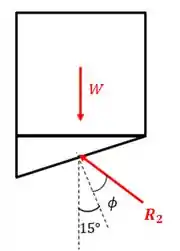
Olhando para o equilíbrio vertical, temos:
Onde é o peso e seu módulo vale:
E sabendo que:
Substituindo esse valor na expressão do equilíbrio vertical, temos:
Passo 3
Agora existe atrito entre a base da cunha e o chão. Com isso, algumas coisas mudarão, mas outras não!!!
Vamos olhar primeiro para o corpo:
Os valores dos ângulos não mudaram, certo?
E nem peso mudou!
Então, o valor de também não mudou. Podemos calcular esse valor da mesma forma que vimos antes:
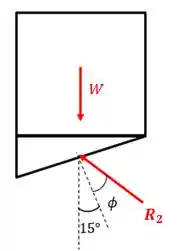
Agora, voltando para o equilíbrio da cunha, vemos um cenário diferente:
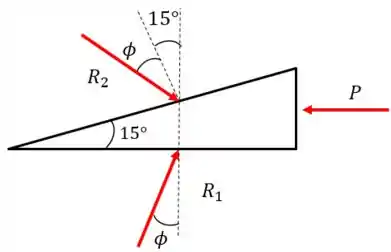
Como você pode ver, agora existe um ângulo entre a reação e a superfície da cunha devido ao atrito. Temos que aplicar o equilíbrio vertical para achar o novo valor de
Mas antes temos que achar as componentes verticais dessas forças que estão inclinadas:
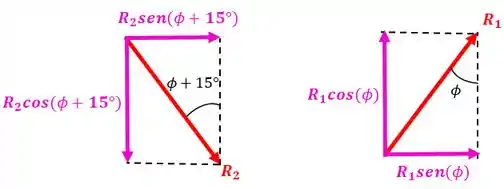
Então, o nosso equilíbrio vertical fica:
Agora, aplicando o equilíbrio horizontal: