Método de Cross
Produzido por Pablo RicardoTeoria
Fala aí, pessoal!! Tudo tranquilo com vocês?
Hoje tô aqui para falar sobre o método de Cross, processo de Cross ou ainda método de distribuição dos momentos. Independentemente do nome esse é um método iterativo baseado no método das deformações para resolver problemas hiperestáticos, aqueles problemas que não conseguimos resolver apenas pelo somatório das forças e dos momentos.
Caso você não saiba um método iterativo é aquele que realizado diversas vezes em “loop” que converge para uma resposta final, muito utilizado pela galerinha de computação.

Vamos ver na prática como vai funcionar isso aí direito então não precisa se preocupar muito por agora.
Distribuição de momentos
A base fundamental deste problema é a distribuição de momentos aplicados a um nó. Imagina um nó submetido a uma carga-momento da seguinte forma:
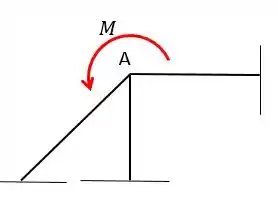
Pessoal, sempre que um momento for exercido sobre um nó vamos considerar esse momento positivo se estiver no sentido horário ok? E negativo se estiver no sentido anti-horário!
Perceba que todas as barras estão engastadas então temos um caso hiperestático. O fundamental do método de Cross é distribuir esse momento em cada barra da seguinte maneira:
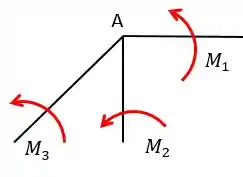
Logicamente que a soma desses momentos deve ser igual a , assim vamos ter:
Aí aqui que entra outra grande sacada deste método é perceber que cada momento , , é proporcional a um termo , e . Esses termos são chamados de coeficientes de distribuição e são calculados com base na rigidez relativa () de cada barra.
Então o coeficiente de distribuição de uma barra é dado pela da barra dividido pela soma da rigidez de todas as barras:
De forma genérica vamos ter:
Dessa forma o momento em cada barra vai ser igual ao momento vezes o coeficiente de distribuição da barra:
Tabelas necessárias
Beleza mas agora restam duas dúvidas, como achar o momento a partir de um problema igual ao apresentado no início e como achar a rigidez relativa das barras. Para isso vamos fazer a utilização de tabelas!

Não, infelizmente não vamos utilizar a tabela de memes =(
Para achar o momento vamos utilizar a tabela de engastamento perfeito que nos dá o momento a partir da configuração das condições dos apoios e de carga que tem essa carinha aqui:
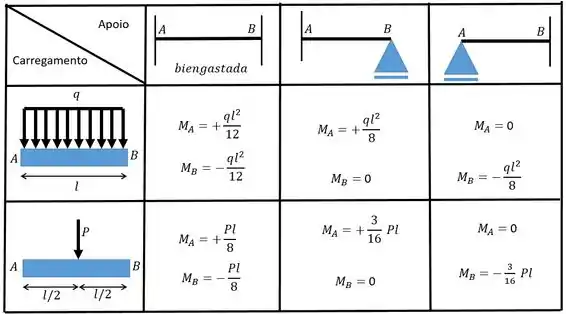
Então se tivermos uma condição de engaste duplo o momento , por exemplo!
Agora para acharmos as constantes de rigidez temos de ir na tabela de grandezas auxiliares para barras com inércia constante:
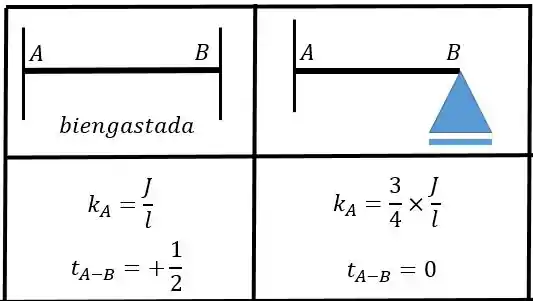
Repare que queremos o minúsculo que é a rigidez relativa! Essa rigidez vai depender da inércia e do comprimento da barra.
Coeficiente de transmissão
Vamos olhar de novo para o nosso nó já com os momentos separados:
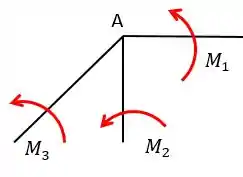
Mas esse não é o sistema todo, correto? Existe ainda os pontos de engaste da barra. Agora vamos descobrir como achar os momentos nesses engastes e para isso vamos utilizar o chamado coeficiente de transmissão, que vai transmitir o momento atuante no nó de uma barra para o seu engaste.
Esse coeficiente aparece na tabela de grandezas auxiliares para barras com inércia constante e é o termo (no caso de um engaste duplo irá valer como mostrado na tabela). Assim vamos ter:
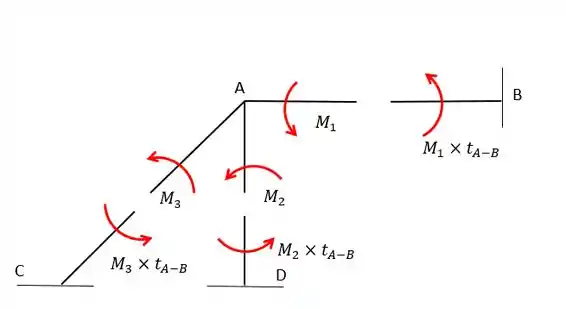
pronto! Agora temos o valor de todos os momentos atuantes na barra! Viu como esse método é bem interessante? A gente pode ainda substituir por valores numéricos para ficar mais fácil de entender:
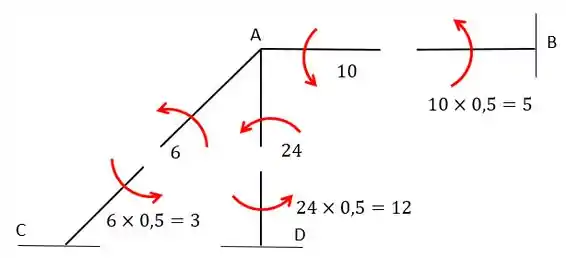
E a iteração?
Galera, eu falei lá no começo que esse método é um método iterativo certo? Que trabalha com repetições e “loops” não é?

Pode ficar calmo que eu não menti para vocês. Na verdade eu apresentei um exemplo com apenas um nó, um ponto de aplicação desse método, de forma que fique mais fácil o entendimento.
As iterações vão aparecer quando a gente precisar aplicar esse método para mais de um nó! Mas vamos ver isso com mais calmo nos exercícios, beleza?
Então partiu resolver alguns!!