Variação de temperatura em Estruturas com Deslocabilidade Externa
Produzido por Pablo RicardoTeoria
Introdução
A ideia dessa aula é ser algo bem rápido, é como se fosse um resumão. A variação de temperatura em estruturas com deslocabilidade externa, é idêntica a variação de temperatura em estruturas com deslocabilidade interna.
O que significa dizer isso? Significa que tudo é exatamente igual? Não, vamos com calma, o que é idêntico é a parte inicial, ou seja, a determinação das deformações devido a variação de temperatura, ou seja, vamos fazer um resuminho bem rápido de tudo que continua igual.
Resumo – O que usamos para determinação de
- A primeira coisa que precisamos lembrar é que se a temperatura no centro de gravidade ( for igual a zero, devemos usar as seguintes fórmulas:
- Caso Bi-engastado
- Caso Engastado e apoiado
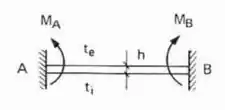
- Quando temos e igual a constante, aí sabemos que temos que seguir outro método, que é o método de Williot, e ele basicamente segue o seguinte passo a passo:
- Passo 1
- Passo 2
- Passo 3
Definimos a origem onde os indeslocaveis também ficam, e vale lembrar que indeslocavel são pontos que não se movem de maneira alguma, tipo os engastes, então se tivéssemos por exemplo um ponto B e um ponto C que fossem engastes, representariamos eles assim.
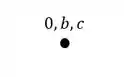
A partir desses indeslocaveis, vamos querer definir um ponto que tenha ambos como predecessores, e fazemos o calculo do deslocamento das barras na direção desse ponto, mas vale lembrar que esses deslocamentos não darão o ponto direto, primeiro darão o número da barra, e só depois achamos o ponto. Por exemplo, suponha que a gente tenha um ponto E que tenha os pontos B e C (na origem) como predecessores, baste então determinar o deslocamento dessas barras com a fórmula . Assim teremos que:
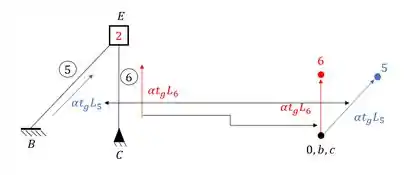
Perceba que com isso não definimos o ponto E mas sim, ou ponto 5 e 6, que representam as barras 5 e 6.
- Passo 1
- Passo 2
- Passo 3
E pasmem, é só isso mesmo que fazemos quando o .
Agora é simples, traçamos retas perpendiculares as barras 5 e 6, e desenhamos essas retas nos pontos 5 e 6 do williot, e com isso, o ponto de encontro será o nosso ponto E:
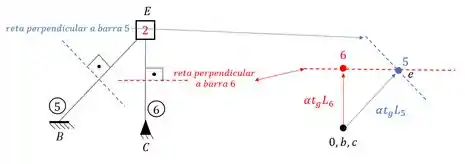
Se fizermos isso para todos os pontos da nossa barra, iremos determinar o que chamamos de williot da nossa estrutura, e com ele, podemos definir as deformações.
Resumo – Regras para determinar as deformações do Williot
Por fim a ultima parte da regra é para saber como determinar a deformação no williot, e é muito simples.
Primeiro devemos renomear as barras de acordo com a ordem de solução dos pontos, por exemplo, no exemplinho ali de cima determinamos primeiro os pontos B e C e só depois determinamos o ponto E, ou seja, a nossa ordem de solução dos pontos é:
Logo o nome das barras seriam: BE (porque achamos o ponto B antes do E) e CE (pelo mesmo motivo dito antes.
Mas porque renomeamos assim? É ai que entram os números do nosso williot.
Por exemplo, se eu quero saber a deformação da barra 6 (que é a barra CE). Primeiro buscamos o numero da barra do nosso williot, que no nosso caso é o ponto 6.
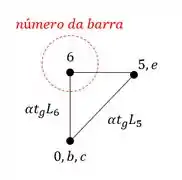
e depois usamos o nome da barra, ou seja, determinamos o segundo termos que compõe o nome da barra no williot, ou seja, o ponto E da barra CE. No nosso williot teremos que:
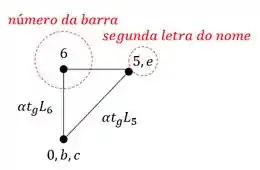
e assim o deslocamento será do número da barra até o segundo termo do nome dela, ou seja, o deslocamento da barra 6 que se chama CE será:
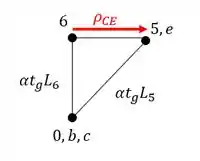
E o que eu quis mostrar com esse exemplinho? Que o williot independe das deslocabilidades, ou seja, se a estrutura tiver deslocabilidades internas ou externas, o cálculo do williot permanece igual.
E a parte nova?
Na verdade a parte nova é a parte velha. Ué, como assim?
O que temos de novo é a deslocabilidade externa, certo? Quando temos deslocabilidade externa o que precisamos?
Precisamos determinar que tipo de coisa ela vai determinar no nosso sistema, se já definimos nos resumos os valores de com as deslocabilidades externas iremos definir
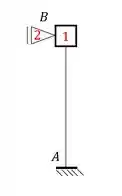
Deslocabilidades externas serão as reações de apoio que tivermos nos nossos apoios de primeiro gênero usados para travamento da estrutura.
O que vale lembrar é que o sentido que definirmos para as reações de apoio, será o mesmo sentido da reação de apoio.
Ou seja, se eu determino uma reação na direção do apoio do primeiro gênero, e essa reação é pra frente, consideramos que a reação no apoio fictício também será pra frente, é bem importante lembrar isso.
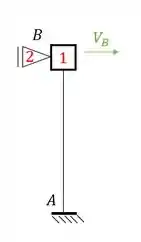
Perceba que no nosso exemplo definimos uma reação de apoio na direção do apoio do primeiro gênero, e ela é pra frente, ou seja, sendo assim iremos definir que a reação no apoio 2 também será pra frente, e vale lembrar que esse sentido é o que definimos como positivo, se desse o contrário, passaríamos para negativo.
O terceiro e ultimo passo é o mais legal, que é basicamente saber qual fórmulas usar para as nossas estruturas com deslocabilidade externa.
Sabemos que sempre que quisermos aplicar uma rotação imposta, que aplicamos em estruturas com deslocabilidade interna, rotacionamos a chapa e usamos as seguintes fórmulas:
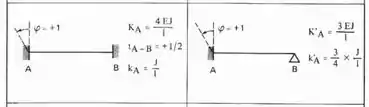
Lembrando que podemos usar 1/EJ para simplificar.
Porém quando temos deslocabilidades externas, não aplicaremos mais rotações impostas, pelo contrário, iremos usar deformações impostas.
Nesse caso a fórmula para o caso de deformações impostas será:
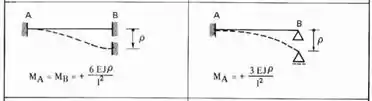
Que é basicamente a fórmula que a gente já ta cansado de usar nas ultimas aulas sobre deslocabilidade externa, tanto pra recalque de apoio, quanto pra carga externa e ainda para apoios elásticos.
Ufa, em fim acabamos essa aula, e você pode ver que essa aula nada mais é que a junção de muitas aulas passadas.
Pegamos um pouquinho da aula de williot, um pouquinho da aula de deslocabilidades externas, e juntamos tudo aqui. Bora fazer exercício então pra gente ficar craque nessa matéria, vamos nessa?
Resumo – Regras para determinar as deformações do Williot
E a parte nova?
Exercícios Resolvidos
Exercício Resolvido #1
Origem do Exercício
Para estrutura abaixo, sabendo que à mesma possui a temperatura das fibras externas igual a e a temperatura das fibras internas igual a , determine o diagrama de momentos fletores da mesma.
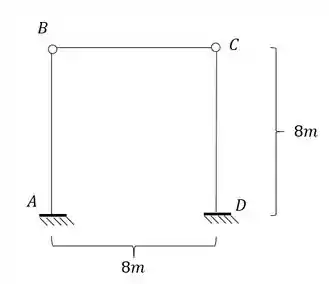
Passo 1
Antes de tudo precisamos saber a temperatura no da nossa estrutura, sabemos que se for diferente de zero, deveremos usar williot, se for igual a zero, teremos que usar as formulazinhas básicas que temos.
Com isso, basta desenharmos o nosso diagrama de temperatura, e vermos no que vai dar, sendo assim teremos que:
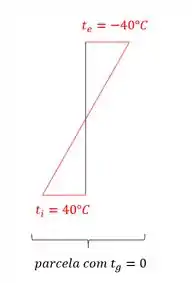
Com isso vemos que a nossa estrutura tem a temperatura no centro de gravidade igual a zero.
Logo as fórmulas que temos que usar são:
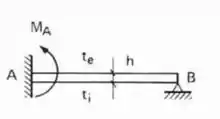
- Caso Bi-engastado
- Caso Engastado e apoiado
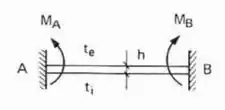
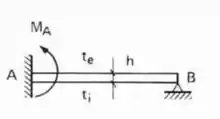
E pasmem, é só isso mesmo que fazemos quando o .
Mas ainda tem uma observação muito importante:
Os sinais dos momentos são feitos levando em consideração que , ou seja, que as temperaturas das fibras internas são maiores que as da externa.
E no nosso caso é exatamente isso que acontece, então podemos ficar tranquilos quanto a isso.
Passo 2
Sabendo qual é o nosso caso, precisamos agora definir as nossas deslocabilidades.
- Analisando primeiro as deslocabilidades internas:
- Sabemos que os pontos A e D são indeslocáveis, logo, não possuem deslocabilidade interna.
- Sabemos também que os pontos B e C são rótulas, logo, também não possuem deslocabilidades internas.
- Então já sabemos que não iremos por chapas na nossa estrutura
- Analisando agora as deslocabilidades externas:
- Veja que os pontos A e D são engastes, então não irão se deslocar, logo, também não temos deslocabilidades externas nesse ponto.
- Porém veja que o ponto B apesar de não poder subir ou descer devido o engaste em A, pode ir pra frente ou pra trás, o que torna ele um ponto deslocavel, e sabemos que nesse tipo de caso precisamos travar esse movimento , especificamente com um apoio do primeiro gênero, dessa maneira teremos que:
- Como o ponto B acabou de se tornar indeslocavel, por consequência, o ponto C se torna indeslocavel também, e com isso passamos a ter apenas uma deslocabilidade na nossa estrutura.
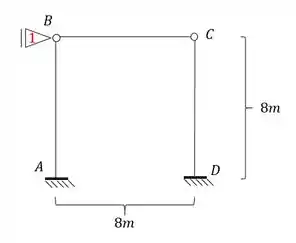
Passo 3
Determinado tudo isso vamos definir o valor de .
Para isso temos que olhar o que acontece com a nossa barra.
Sabendo que a barra AB e CD apresentam o mesmo comportamento estrutural, podemos ver que de um lado temos o engaste e do outro temos um apoio (representado pela rótula e pelo apoio do primeiro gênero, ou seja, podemos considerar essa barra do tipo engastada e apoiada, e a fórmula a ser usada nela é:
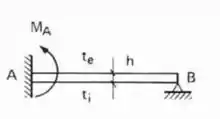
E aplicando isso a nossa estrutura teremos que:
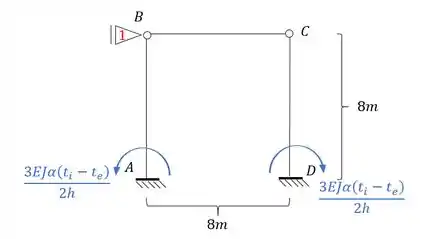
Perceba que a barra BC não possui nenhum tipo de momento, isso porque ela representa uma barra biapoiada, logo, não possui momentos de rigidez.
Substituindo os valores teremos que:
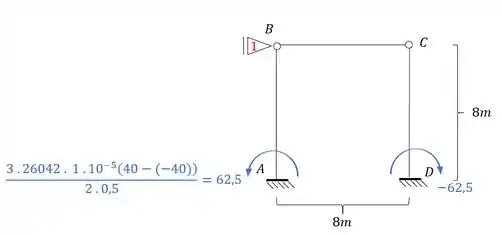
E assim teremos que determinar a reação de apoio que será feito por:
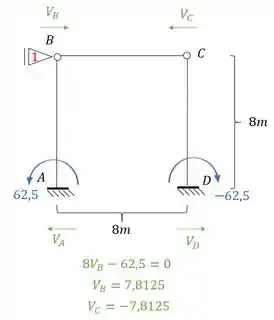
Passo 4
Agora só precisamos definir para termos o nosso sistema completo. Para isso sabemos que temos que deslocar o nosso apoio, e deslocando o apoio, usamos a seguinte fórmula:
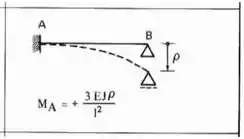
Fazendo esse deslocamento na nossa estrutura teremos que:
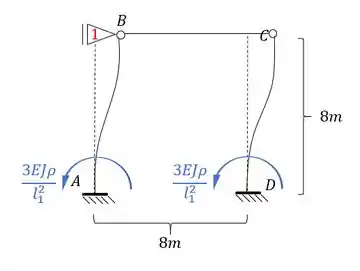
Como fizemos um deslocamento imposto, podemos dar o valor que quisermos pra ele, que no nosso caso pode ser dado por:
Usando também o nosso conceito de rigidez relativa podemos dividir o nosso momento por EJ, e com isso restaria apenas:
Como temos o comprimento da barra fica fácil, e com isso teremos que:
E esse será o nosso valor de momento, mas qual é o nosso objetivo? É determinar a reação de apoio, porque vai ser a reação de apoio que vai nós dar o valor de . Mas temos que tomar cuidado, porque veja que temos momentos de ambos os lados, e ambos produziram reações horizontais, e precisamos contabilizar a contribuição dos dois, sendo assim teremos que:
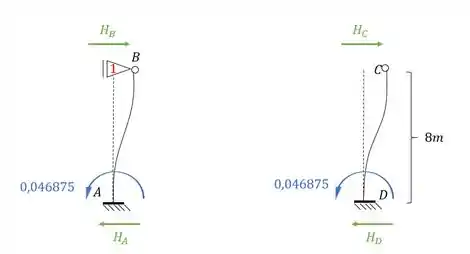
Perceba que precisamos dos valores de e . Com isso teremos que:
Mas lembre-se que . Sendo assim teremos que:
Passo 5
Agora que já fizemos a parte mais difícil, basta montarmos o nosso sistema de equações que será:
Resolvendo esse sistema teremos que:
Para determinação dos momentos fletores, precisamos do momento fletor de todos os nós em todas as barras em todos os sistemas, dessa forma a primeira coisa que devemos fazer é analisar cada sistema.
- Sistema 0
- Sistema 1
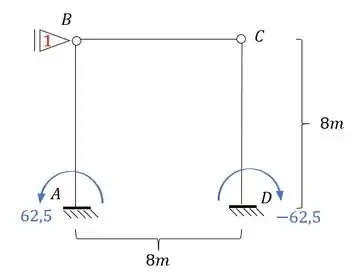
Uma coisa mega importante é lembrar de usar o fator de rigidez relativa EM TODOS OS CASOS que temos para o sistema 1, se não vamos errar, como já fizemos isso:

E usando a nossa fórmula para cada nó teremos que:
Perceba que já temos os momentos de cada nó da nossa estrutura, e para cada barra, sendo assim se desenharmos isso na nossa estrutura teremos que:
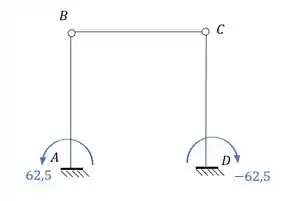
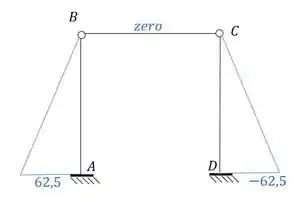
Resposta
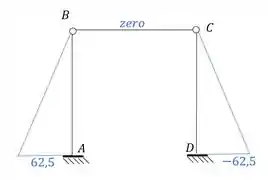
Exercício Resolvido #2
Origem do Exercício
Para estrutura abaixo, sabendo que à mesma possui a temperatura das fibras externas igual a e a temperatura das fibras internas igual a , determine o diagrama de momentos fletores da mesma.
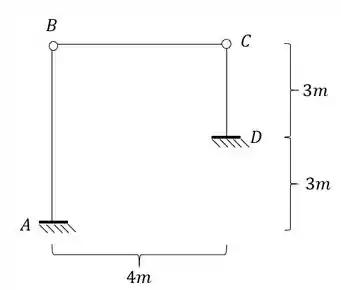
Passo 1
Antes de tudo precisamos saber a temperatura no da nossa estrutura, sabemos que se for diferente de zero, deveremos usar williot, se for igual a zero, teremos que usar as formulazinhas básicas que temos.
Com isso, basta desenharmos o nosso diagrama de temperatura, e vermos no que vai dar, sendo assim teremos que:
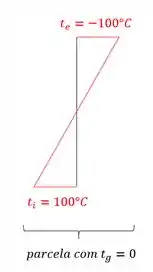
Com isso vemos que a nossa estrutura tem a temperatura no centro de gravidade igual a zero.
Logo as fórmulas que temos que usar são:
- Caso Bi-engastado
- Caso Engastado e apoiado
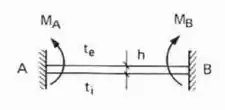
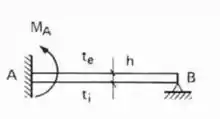
E pasmem, é só isso mesmo que fazemos quando o .
Mas ainda tem uma observação muito importante:
Os sinais dos momentos são feitos levando em consideração que , ou seja, que as temperaturas das fibras internas são maiores que as da externa.
E no nosso caso é exatamente isso que acontece, então podemos ficar tranquilos quanto a isso.
Passo 2
Sabendo qual é o nosso caso, precisamos agora definir as nossas deslocabilidades.
- Analisando primeiro as deslocabilidades internas:
- Sabemos que os pontos A e D são indeslocáveis, logo, não possuem deslocabilidade interna.
- Sabemos também que os pontos B e C são rótulas, logo, também não possuem deslocabilidades internas.
- Então já sabemos que não iremos por chapas na nossa estrutura
- Analisando agora as deslocabilidades externas:
- Veja que os pontos A e D são engastes, então não irão se deslocar, logo, também não temos deslocabilidades externas nesse ponto.
- Porém veja que o ponto B apesar de não poder subir ou descer devido o engaste em A, pode ir pra frente ou pra trás, o que torna ele um ponto deslocavel, e sabemos que nesse tipo de caso precisamos travar esse movimento , especificamente com um apoio do primeiro gênero, dessa maneira teremos que:
- Como o ponto B acabou de se tornar indeslocavel, por consequência, o ponto C se torna indeslocavel também, e com isso passamos a ter apenas uma deslocabilidade na nossa estrutura.
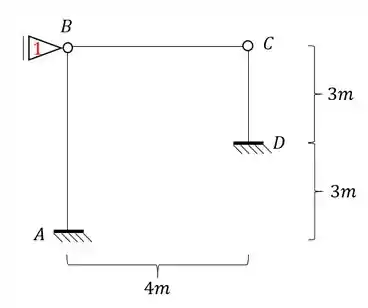
Passo 3
Determinado tudo isso vamos definir o valor de .
Para isso temos que olhar o que acontece com a nossa barra.
Sabendo que a barra AB e CD apresentam o mesmo comportamento estrutural, podemos ver que de um lado temos o engaste e do outro temos um apoio (representado pela rótula e pelo apoio do primeiro gênero, ou seja, podemos considerar essa barra do tipo engastada e apoiada, e a fórmula a ser usada nela é:
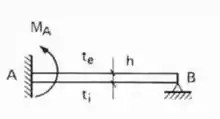
E aplicando isso a nossa estrutura teremos que:
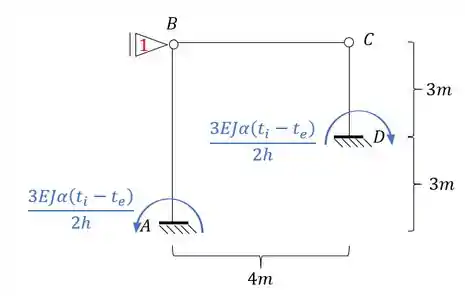
Perceba que a barra BC não possui nenhum tipo de momento, isso porque ela representa uma barra biapoiada, logo, não possui momentos de rigidez.
Substituindo os valores teremos que:
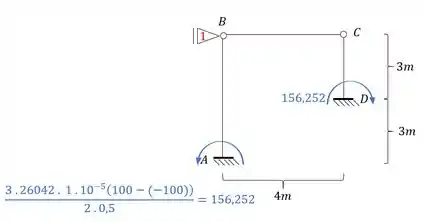
E assim teremos que determinar a reação de apoio que será feito por:
Passo 4
Agora só precisamos definir para termos o nosso sistema completo. Para isso sabemos que temos que deslocar o nosso apoio, e deslocando o apoio, usamos a seguinte fórmula:
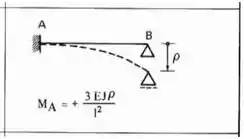
Fazendo esse deslocamento na nossa estrutura teremos que:
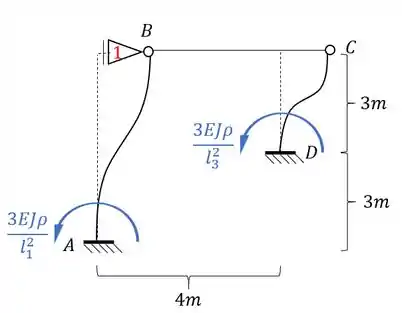
Como fizemos um deslocamento imposto, podemos dar o valor que quisermos pra ele, que no nosso caso pode ser dado por:
Usando também o nosso conceito de rigidez relativa podemos dividir o nosso momento por EJ, e com isso restaria apenas:
Como temos o comprimento da barra fica fácil, e com isso teremos que:
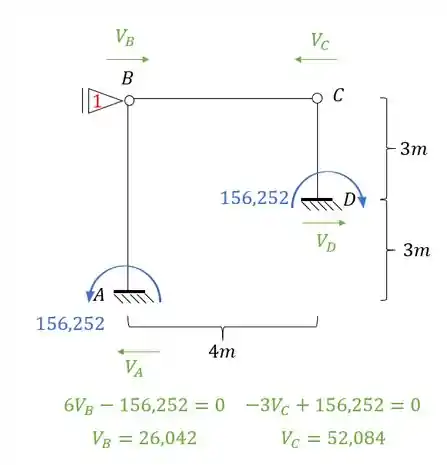
E esse será o nosso valor de momento, mas qual é o nosso objetivo? É determinar a reação de apoio, porque vai ser a reação de apoio que vai nós dar o valor de . Mas temos que tomar cuidado, porque veja que temos momentos de ambos os lados, e ambos produziram reações horizontais, e precisamos contabilizar a contribuição dos dois, sendo assim teremos que:
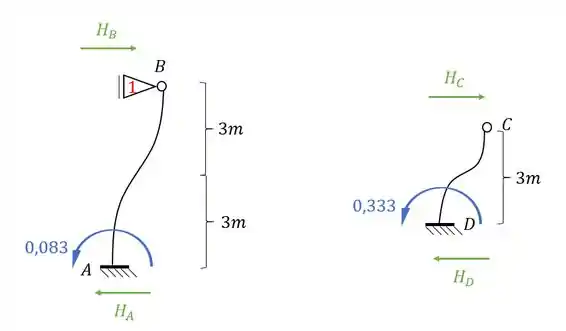
Perceba que precisamos dos valores de e . Com isso teremos que:
Para teremos que:
Passo 5
Agora que já fizemos a parte mais difícil, basta montarmos o nosso sistema de equações que será:
Resolvendo esse sistema teremos que:
Para determinação dos momentos fletores, precisamos do momento fletor de todos os nós em todas as barras em todos os sistemas, dessa forma a primeira coisa que devemos fazer é analisar cada sistema.
- Sistema 0
- Sistema 1
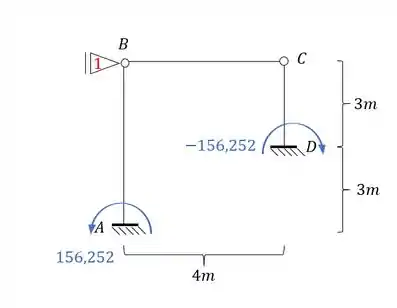
Uma coisa mega importante é lembrar de usar o fator de rigidez relativa EM TODOS OS CASOS que temos para o sistema 1, se não vamos errar, como já fizemos isso:
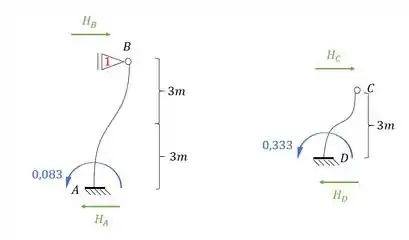
E usando a nossa fórmula para cada nó teremos que:
Perceba que já temos os momentos de cada nó da nossa estrutura, e para cada barra, sendo assim se desenharmos isso na nossa estrutura teremos que:
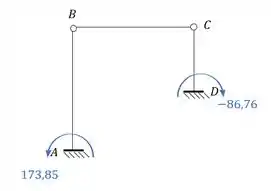
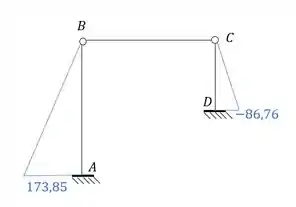
Resposta
Exercício Resolvido #3
Origem do Exercício
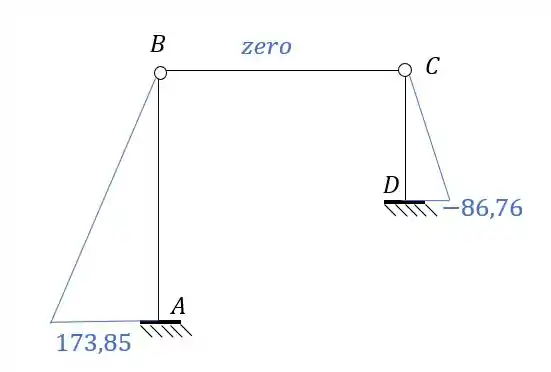
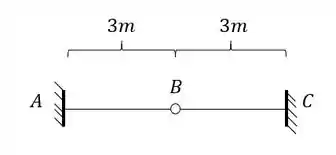
Para estrutura abaixo, sabendo que à mesma possui a temperatura das fibras externas igual a e a temperatura das fibras internas igual a , determine o diagrama de momentos fletores da mesma. Além disso determine a deformação vertical do ponto B.
Passo 1
Antes de tudo precisamos saber a temperatura no da nossa estrutura, sabemos que se for diferente de zero, deveremos usar williot, se for igual a zero, teremos que usar as formulazinhas básicas que temos.
Com isso, basta desenharmos o nosso diagrama de temperatura, e vermos no que vai dar, sendo assim teremos que:
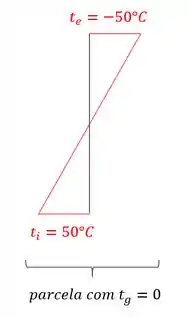
Com isso vemos que a nossa estrutura tem a temperatura no centro de gravidade igual a zero.
Logo as fórmulas que temos que usar são:
- Caso Bi-engastado
- Caso Engastado e apoiado
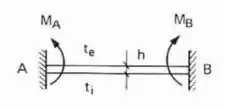
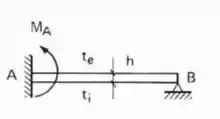
E pasmem, é só isso mesmo que fazemos quando o .
Mas ainda tem uma observação muito importante:
Os sinais dos momentos são feitos levando em consideração que , ou seja, que as temperaturas das fibras internas são maiores que as da externa.
E no nosso caso é exatamente isso que acontece, então podemos ficar tranquilos quanto a isso.
Passo 2
Sabendo qual é o nosso caso, precisamos agora definir as nossas deslocabilidades.
- Analisando primeiro as deslocabilidades internas:
- Sabemos que os pontos A e C são indeslocáveis, logo, não possuem deslocabilidade interna.
- Sabemos também que o ponto B é uma rótula, logo, também não possui deslocabilidade interna.
- Então já sabemos que não iremos por chapas na nossa estrutura
- Analisando agora as deslocabilidades externas:
- Veja que os pontos A e C são engastes, então não irão se deslocar, logo, também não temos deslocabilidades externas nesse ponto.
- Porém veja que o ponto B apesar de não poder ir para esquerda ou direita devido o engaste em A e B, pode ir pra cima ou para baixo, o que torna ele um ponto deslocavel, e sabemos que nesse tipo de caso precisamos travar esse movimento , especificamente com um apoio do primeiro gênero, dessa maneira teremos que:
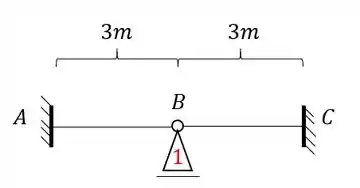
Passo 3
Determinado tudo isso vamos definir o valor de .
Para isso temos que olhar o que acontece com a nossa barra.
Sabendo que a barra AB e BC apresentam o mesmo comportamento estrutural, podemos ver que de um lado temos o engaste e do outro temos um apoio (representado pela rótula e pelo apoio do primeiro gênero, ou seja, podemos considerar essa barra do tipo engastada e apoiada, e a fórmula a ser usada nela é:
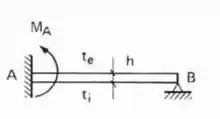
E aplicando isso a nossa estrutura teremos que:
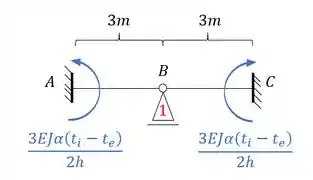
Perceba que a barra BC não possui nenhum tipo de momento, isso porque ela representa uma barra biapoiada, logo, não possui momentos de rigidez.
Substituindo os valores teremos que:
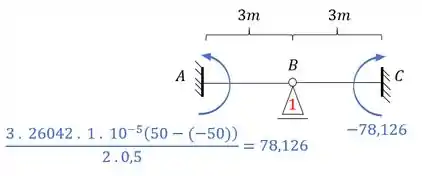
E assim teremos que determinar a reação de apoio que será feito por:
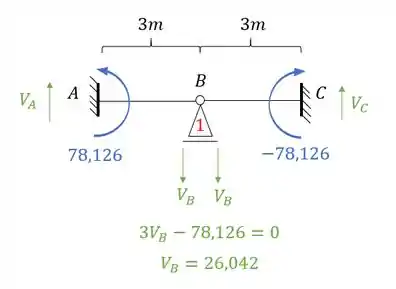
Perceba que temos duas reações de apoio, e que elas deram pra baixo (que é o nosso sentido negativo), dessa maneira teremos que:
Passo 4
Agora só precisamos definir para termos o nosso sistema completo. Para isso sabemos que temos que deslocar o nosso apoio, e deslocando o apoio, usamos a seguinte fórmula:
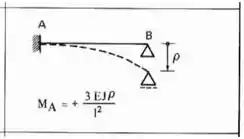
Fazendo esse deslocamento na nossa estrutura teremos que:
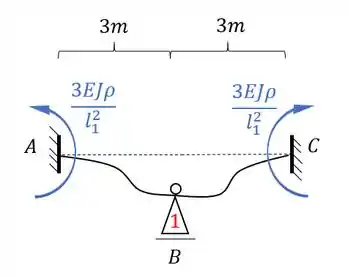
Como fizemos um deslocamento imposto, podemos dar o valor que quisermos pra ele, que no nosso caso pode ser dado por:
Usando também o nosso conceito de rigidez relativa podemos dividir o nosso momento por EJ, e com isso restaria apenas:
Como temos o comprimento da barra fica fácil, e com isso teremos que:
E esse será o nosso valor de momento, mas qual é o nosso objetivo? É determinar a reação de apoio, porque vai ser a reação de apoio que vai nós dar o valor de . Mas temos que tomar cuidado, porque veja que temos momentos de ambos os lados, e ambos produziram reações verticais, e precisamos contabilizar a contribuição dos dois, sendo assim teremos que:
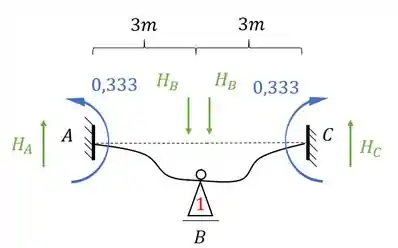
Perceba que precisamos dos valores de e . Com isso teremos que:
Como temos dois e eles são para baixo, significa que na nossa escolha de sinais eles serão negativos:
Passo 5
Agora que já fizemos a parte mais difícil, basta montarmos o nosso sistema de equações que será:
Resolvendo esse sistema teremos que:
Para determinação dos momentos fletores, precisamos do momento fletor de todos os nós em todas as barras em todos os sistemas, dessa forma a primeira coisa que devemos fazer é analisar cada sistema.
- Sistema 0
- Sistema 1
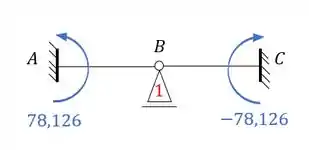
Uma coisa mega importante é lembrar de usar o fator de rigidez relativa EM TODOS OS CASOS que temos para o sistema 1, se não vamos errar, como já fizemos isso:
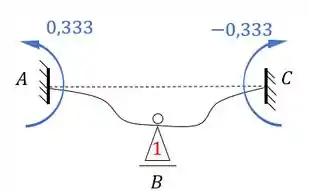
E usando a nossa fórmula para cada nó teremos que:
Perceba que já temos os momentos de cada nó da nossa estrutura, e para cada barra, sendo assim se desenharmos isso na nossa estrutura teremos que:
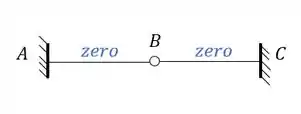
Lembre-se que dividimos todos os fatores por EJ, ou seja, se quisermos saber o valor real do deslocamento vertical, precisamos repor isso que tirarmos, dessa forma teremos que:
Resposta
Exercício Resolvido #4
Origem do Exercício
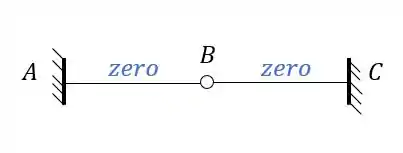
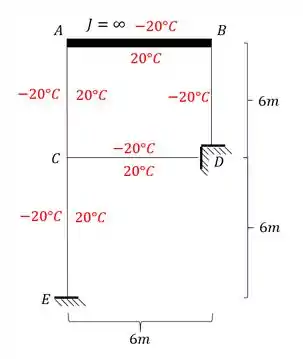
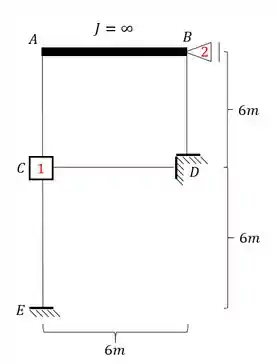
Para estrutura abaixo, sabendo que à mesma possui a temperatura das fibras externas igual a e a temperatura das fibras internas igual a , determine a deformação horizontal do ponto B.
Passo 1
Antes de tudo precisamos saber a temperatura no da nossa estrutura, sabemos que se for diferente de zero, deveremos usar williot, se for igual a zero, teremos que usar as formulazinhas básicas que temos.
Com isso, basta desenharmos o nosso diagrama de temperatura, e vermos no que vai dar, sendo assim teremos que:
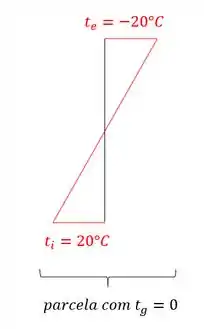
Com isso vemos que a nossa estrutura tem a temperatura no centro de gravidade igual a zero.
Logo as fórmulas que temos que usar são:
- Caso Bi-engastado
- Caso Engastado e apoiado
- Analisando primeiro as deslocabilidades internas:
- Sabemos que os pontos E e D são indeslocáveis, logo, não possuem deslocabilidade interna.
- O ponto C não é nem rótula e nem apoio extremo, logo possuirá uma deslocabilidade interna. E sabemos que se possuímos deslocabilidade interna, temos obrigatoriamente que travar ela com uma chapa, sendo assim teremos que:
- Agora que vem o diferencial. Os pontos A e B estão nas extremidades da barra com inércia infinita. SEMPRE que tivermos uma barra com inércia infinita, ela obrigatoriamente tornará os nós da sua extremidade indeslocaveis com relação a rotação. Ou seja, os nós A e B não podem rotacionar porque a barra AB possui uma inércia taõ grande que já vai impedir isso. Ou seja, só temos 1 deslocabilidade interna.
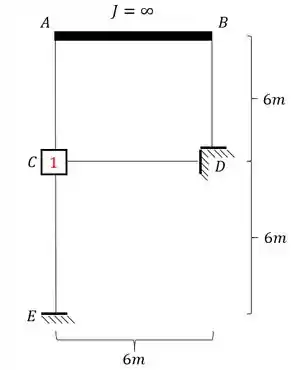
- Analisando agora as deslocabilidades externas:
- Os pontos E e D são engastes, logo são considerados indeslocaveis.
- O ponto C também pode ser considerado assim, além do mais, não pode nem se deslocar pra baixo e pra cima, e nem da esquerda para direita ou vice versa.
- O ponto B também não pode se deslocar na vertical, porém pode claramente se deslocar na horizontal, por isso devemos travar ele nesse sentido, com o nosso velho amigo apoio do primeiro gênero.
- Com o ponto B travado podemos ver que passamos a ter o ponto A indeslocavel, logo teremos apenas 1 deslocabilidade externa mesmo.
- Caso Bi-engastado
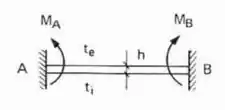
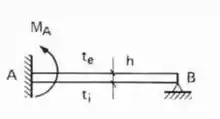
E pasmem, é só isso mesmo que fazemos quando o .
Mas ainda tem uma observação muito importante:
Os sinais dos momentos são feitos levando em consideração que , ou seja, que as temperaturas das fibras internas são maiores que as da externa.
E no nosso caso é exatamente isso que acontece, então podemos ficar tranquilos quanto a isso.
Passo 2
Sabendo qual é o nosso caso, precisamos agora definir as nossas deslocabilidades.
Passo 3
Determinado tudo isso vamos definir o valor de e .
Perceba que todas as barras ou possuem na sua extremidade, ou uma chapa, ou um engaste ou uma barra de inércia infinita que sabemos que impede rotação. Dessa maneira a nossa estrutura pode ser definida como um tipo de estrutura Bi-engastada.
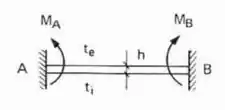
E aplicando isso a nossa estrutura teremos que:
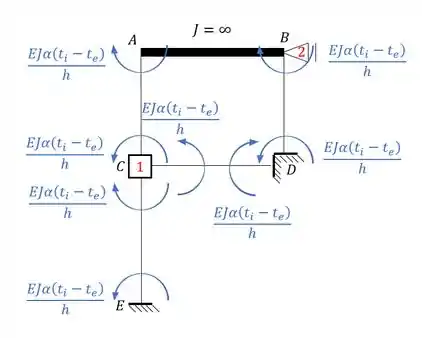
Substituindo os valores teremos que:
Com esse valor conseguimos determinar o valor de
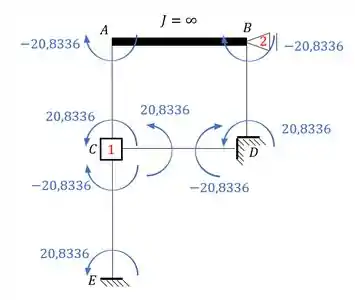
E para determinarmos teremos que determinar a reação de apoio que receberá contribuição apenas das barras AC e BD.
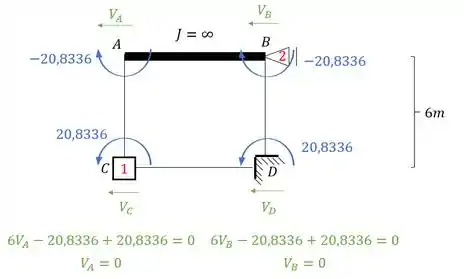
Perceba que temos duas reações de apoio, e que elas deram pra baixo (que é o nosso sentido negativo), dessa maneira teremos que:
Passo 2
Agora que definimos as rigidezes do sistema zero, precisamos determinar nos sistemas com a deformação de cada um dos travamentos, sendo assim teremos que:
Sabemos que para definir é muito simples, como se trata de uma chapa, basta rotacionarmos ela em 1 grau, que sempre rotacionamos no sentido anti-horário para sempre termos esse valor positivo.
Como todas as extremidades são engastadas, e até mesmo os pontos A e B representam engastes, então teremos que a fórmula a ser usada é:
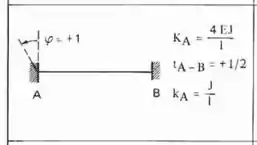
Fazendo isso na nossa estrutura teremos que:
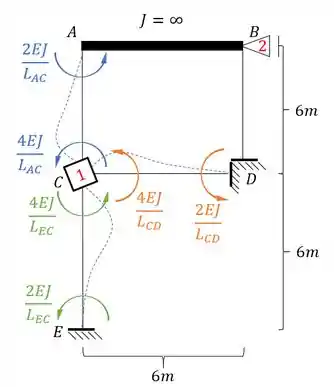
Sendo assim o valor de será:
Sabemos que podemos usar rigidez relativa para facilitar as nossas contas, que podemos usar:
Sendo assim teremos que:
Para determinar o valor é muito simples, é só determinarmos a reação de apoio que age no nosso ponto 2.
Veja que somente as barras EC e CA produziram reações na horizontal. Porém apenas a barra CA irá interferir no nosso apoio em 2, por isso iremos calcular apenas a reação de apoio referente a ela, sendo assim teremos que:
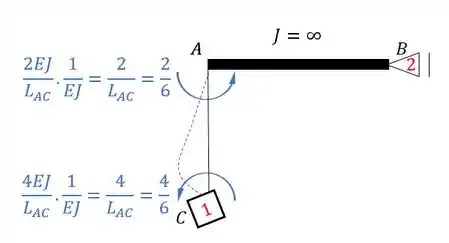
Marcando as reações teremos que:
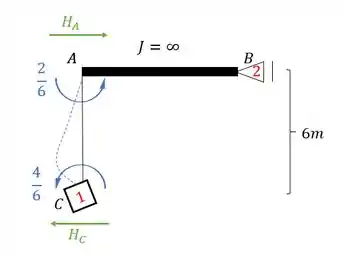
E aqui temos uma diferença importante, o sentido da reação nesse caso, é o mesmo da força calculada, ou seja, se está pra frente, e na mesma direção do apoio 2, então a reação em 2 vai ser pra frente também e com o mesmo valor de . Sendo assim teremos que:
Passo 4
Agora que definimos as rigidezes do sistema 1, precisamos determinar no sistema 2. Como o sistema 2 é um apoio iremos precisar usar o conceito de deformação e não amis de rotação.
Sabemos que para definir é muito simples, como se trata de uma chapa, basta analisarmos o momento que aparecerá nela após a deformação de 1 unidade.
Como todas as extremidades são engastadas, e até mesmo os pontos A e B representam engastes, então teremos que a fórmula a ser usada é:
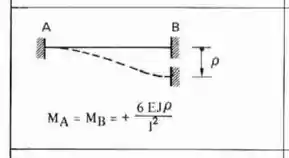
Fazendo o deslocamento na nossa estrutura teremos que:
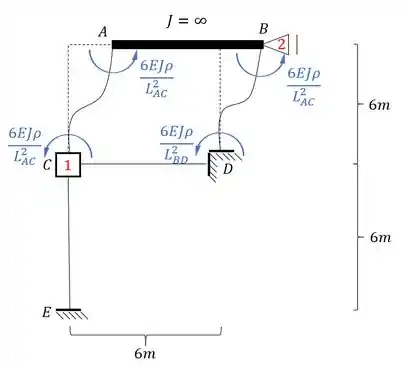
Sendo assim o valor de será:
Sabemos que podemos usar rigidez relativa para facilitar as nossas contas, que podemos usar:
E também podemos usar que:
Sendo assim teremos que:
Para determinar o valor é muito simples, é só determinarmos a reação de apoio que age no nosso ponto 2.
Veja que somente as barras CA e DB produziram reações na horizontal, por isso iremos calcular apenas a reação de apoio referente a elas, sendo assim teremos que:
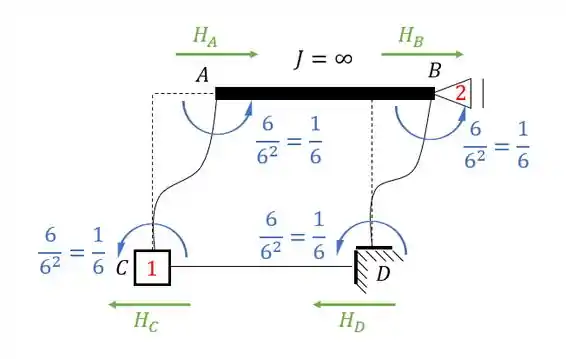
E aqui temos uma diferença importante, o sentido da reação nesse caso, é o mesmo da força calculada, ou seja, se e estão pra frente, e na mesma direção do apoio 2, então a reação em 2 vai ser pra frente também e com o mesmo valor de . Sendo assim teremos que:
Passo 3
Resolvendo o nosso sistema vamos ter que:
Substituindo teremos que:
Nosso objetivo era determinar a deformação horizontal do ponto B, que é exatamente o ponto que colocamos o apoio do primeiro gênero 2, que nós da o .
Vale lembrar que também dividimos tudo por EJ, ou seja, precisamos dividir aqui para termos o resultado real.
Resposta
Exercício Resolvido #5
Origem do Exercício
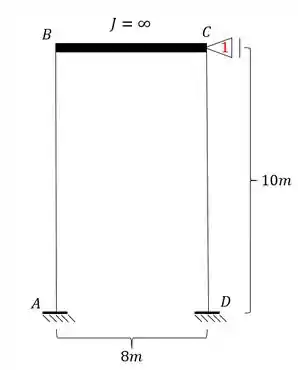
Para estrutura abaixo, sabendo que à mesma possui a temperatura das fibras externas igual a e a temperatura das fibras internas igual a , determine a deformação horizontal do ponto C.
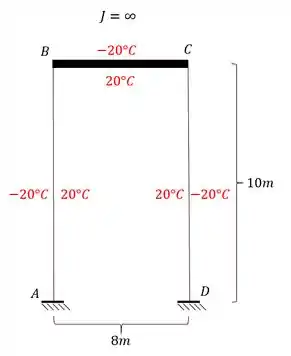
Passo 1
Antes de tudo precisamos saber a temperatura no da nossa estrutura, sabemos que se for diferente de zero, deveremos usar williot, se for igual a zero, teremos que usar as formulazinhas básicas que temos.
Com isso, basta desenharmos o nosso diagrama de temperatura, e vermos no que vai dar, sendo assim teremos que:
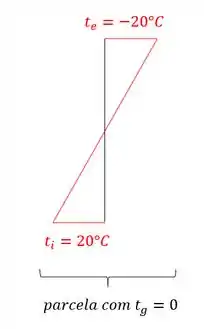
Com isso vemos que a nossa estrutura tem a temperatura no centro de gravidade igual a zero.
Logo as fórmulas que temos que usar são:
- Caso Bi-engastado
- Caso Engastado e apoiado
- Analisando primeiro as deslocabilidades internas:
- Sabemos que os pontos A e D são indeslocáveis, logo, não possuem deslocabilidade interna.
- Agora que vem o diferencial. Os pontos C e B estão nas extremidades da barra com inércia infinita. SEMPRE que tivermos uma barra com inércia infinita, ela obrigatoriamente tornará os nós da sua extremidade indeslocaveis com relação a rotação. Ou seja, os nós C e B não podem rotacionar porque a barra CB possui uma inércia tão grande que já vai impedir isso. Ou seja, não temos deslocabilidade interna.
- Analisando agora as deslocabilidades externas:
- Os pontos A e D são engastes, logo são considerados indeslocaveis.
- O ponto C também não pode se deslocar na vertical, porém pode claramente se deslocar na horizontal, por isso devemos travar ele nesse sentido, com o nosso velho amigo apoio do primeiro gênero.
- Com o ponto C travado podemos ver que passamos a ter o ponto B indeslocavel, logo teremos apenas 1 deslocabilidade externa mesmo.
- Caso Bi-engastado
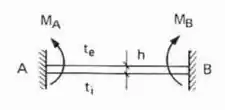
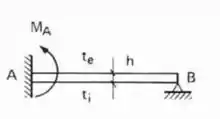
E pasmem, é só isso mesmo que fazemos quando o .
Mas ainda tem uma observação muito importante:
Os sinais dos momentos são feitos levando em consideração que , ou seja, que as temperaturas das fibras internas são maiores que as da externa.
E no nosso caso é exatamente isso que acontece, então podemos ficar tranquilos quanto a isso.
Passo 2
Sabendo qual é o nosso caso, precisamos agora definir as nossas deslocabilidades.
Passo 3
Determinado tudo isso vamos definir o valor de .
Perceba que todas as barras ou possuem na sua extremidade, ou um engaste ou uma barra de inércia infinita que sabemos que impede rotação. Dessa maneira a nossa estrutura pode ser definida como um tipo de estrutura Bi-engastada.
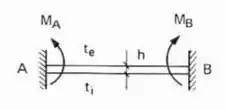
E aplicando isso a nossa estrutura teremos que:
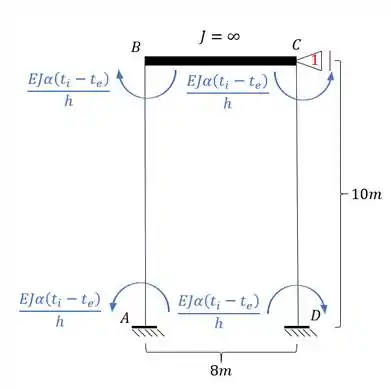
Substituindo os valores teremos que:
E para determinarmos teremos que determinar a reação de apoio que receberá contribuição apenas das barras AB e CD.
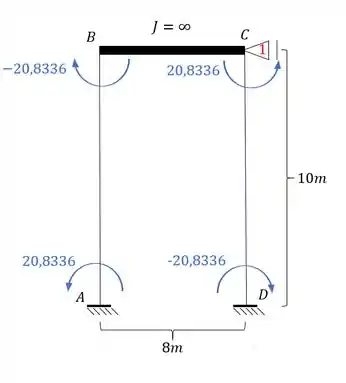
Calculando as reações teremos que:
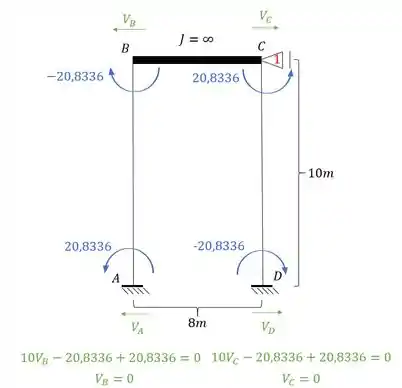
Perceba que temos duas reações de apoio, e que elas deram pra baixo (que é o nosso sentido negativo), dessa maneira teremos que:
Passo 2
Agora que definimos as rigidezes do sistema zero, precisamos determinar nos sistemas com a deformação de cada um dos travamentos, sendo assim teremos que:
Para determinar o valor é muito simples, é só determinarmos a reação de apoio que age no nosso ponto 1.
Como temos que deslocar o nosso apoio em 1, e sabemos que todos os nossos nós são engastes, usaremos a seguinte fórmula:
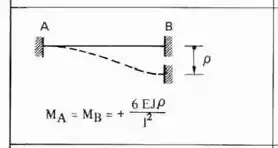
Colocando o deslocamento na nossa estrutura teremos que:
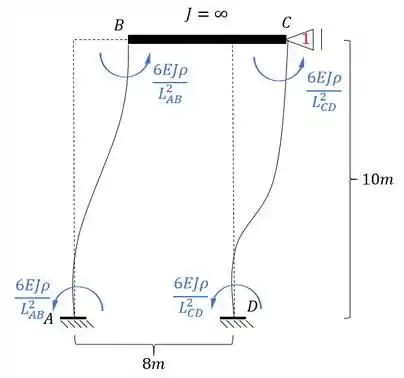
Usando o fator de rigidez relativa teremos que:
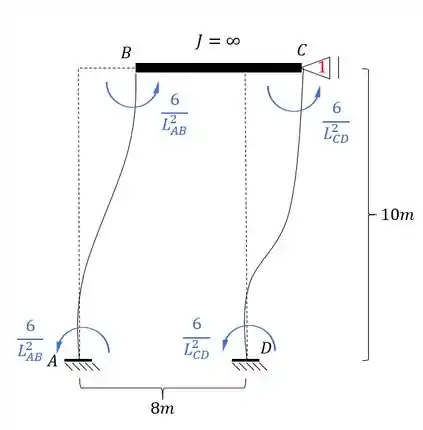
Como todos os comprimentos são iguais teremos que:
Veja que somente as barras AB e DC produziram reações na horizontal, por isso iremos calcular apenas a reação de apoio referente a elas, sendo assim teremos que:
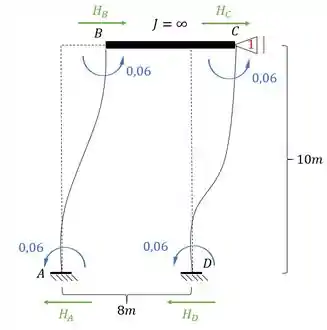
E aqui temos uma diferença importante, o sentido da reação nesse caso, é o mesmo da força calculada, ou seja, se e estão pra frente, e na mesma direção do apoio 1, então a reação em 1 vai ser pra frente também e com o mesmo valor de . Sendo assim teremos que:
Passo 3
Resolvendo o nosso sistema vamos ter que:
Substituindo teremos que:
Nosso objetivo era determinar a deformação horizontal do ponto B, que é exatamente o ponto que colocamos o apoio do primeiro gênero 1, que nós da o .
Vale lembrar que também dividimos tudo por EJ, ou seja, precisamos dividir aqui para termos o resultado real.
Ou seja, pela simetria da estrutura e do carregamento de temperatura, o ponto B não sofre deslocamentos.