Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Dinâmica Volume 2 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 7.11 - Ex. 124

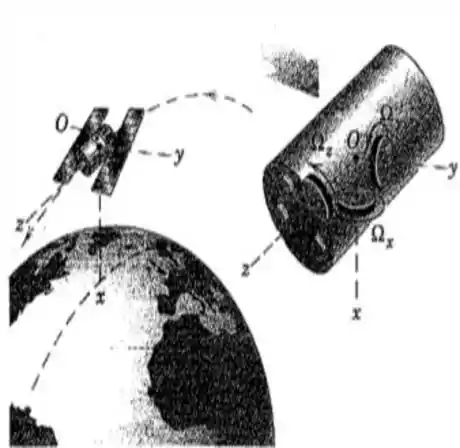
124. O satélite de observação da Terra está em uma órbita circular de período τ . A velocidade angular do satélite em torno de seu eixo y ou eixo de arfagem é ω = 2 π / τ , e as velocidades angulares em torno dos eixos x e z são nulas. Desse modo, o eixo x do satélite aponta sempre para o centro da terra. O satélite possui um sistema de controle da orientação angular com volantes de reação, constituído pelos três volantes mostrados, cada um dos quais pode receber um torque variável de seu motor individual. A velocidade angular Ω z do volante z em relação ao satélite é Ω 0 no instante de tempo t = 0 , e os volantes x e y estão em repouso em relação ao satélite t = 0 . Determine os torques axiais M x , M y   e   M z que devem ser exercidos pelos motores sobre os eixos de seus respectivos volantes a fim de que a velocidade angular ω do satélite permaneça constante. O momento de inércia de cada volante de reação em relação ao seu eixo é I . As velocidades dos volantes de reação x e z são funções harmônicas do tempo, com um período igual ao da órbita. Represente graficamente as variações dos torques e as velocidades relativas dos volantes Ω x , Ω y   e   Ω z como funções do tempo durante um período da órbita. (Sugestão: O torque para acelerar o volante x é igual à reação do momento giroscópico sobre o volante z , e vice-versa).

Passo 1

Bom, primeiro a gente vai montar um diagrama de momentos para o sistema:

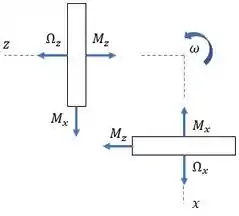
E estabelecer algumas condições para t = 0 :

Ω z = Ω 0

Ω ˙ z = 0

Ω x = 0

Passo 2

Agora, vamos definir o que é cada momento representado no desenho.

M x é o momento giroscópico no eixo z e é dado por:

M x = I Ω z ω

- M x é o momento para acelerar o eixo x :

- M x = I Ω ˙ x

Assim, podemos relacionar:

I Ω z ω = - I Ω ˙ x

∴ Ω ˙ x + Ω z ω = 0   ( I )

M z é o momento giroscópico no eixo x e é dado por:

M z = - I Ω x ω

- M z é o momento para acelerar o eixo z :

- M z = I Ω ˙ z

Assim, podemos relacionar:

I Ω x ω = - I Ω ˙ z

∴ Ω ˙ z + Ω x ω = 0   ( I I )

Passo 3

Se derivarmos a equação ( I ) , obtemos:

d d t Ω ˙ x + d d t Ω z ω = d d t 0

Ω ¨ x + Ω ˙ z ω = 0

Mas da equação ( I I ) , temos:

Ω ˙ z = - Ω x ω

O que nos resulta em:

Ω ¨ x + - ω 2 Ω x = 0

De modo semelhante para a equação ( I I ) :

d d t Ω ˙ z + d d t Ω x ω = d d t 0

Ω ¨ z + Ω ˙ x ω = 0

Ω ˙ x = - Ω z ω

∴ Ω ¨ z - ω 2 Ω ˙ z = 0

Passo 4

Pelas condições do Passo 1 para t = 0 :

Ω x = - Ω 0 ⋅ s e n ( ω t )

Ω z = Ω 0 ⋅ c o s ( ω t )

Passo 5

Substituindo as variáveis encontradas nas equações de momento dos torques dos eixos:

M x = - I ω Ω 0 ⋅ c o s ( ω t )

M z = - I ω Ω 0 ⋅ s e n ( ω t )

Passo 6

E calculando o momento total por Pitágoras:

M = M x 2 + M z 2

M = ( - I ω Ω 0 ⋅ c o s ( ω t ) ) 2 + ( - I ω Ω 0 ⋅ s e n ( ω t ) ) 2

M = I 2 ω 2 Ω 0 2 ⋅ c o s ( ω t ) 2 + I 2 ω 2 Ω 0 2 ⋅ s e n ( ω t ) 2

M = I 2 ω 2 Ω 0 2 ⋅ ( cos ⁡ ω t 2 + ( s e n ω t ) 2 )

Como sabemos que:

( cos ⁡ θ ) 2 + ( s e n θ ) 2 = 1

M = I 2 ω 2 Ω 0 2

∴ M = I ω Ω 0   ( C o n s t a n t e )

Resposta

Os torques axiais são:

M x = - I ω Ω 0 ⋅ c o s ( ω t )

M z = - I ω Ω 0 ⋅ s e n ( ω t )

Gráfico da variação da velocidade relativa dos volantes em função do tempo:

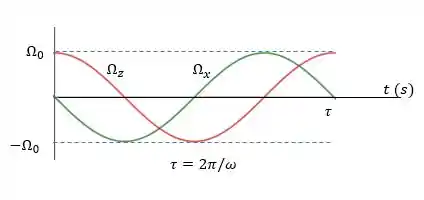
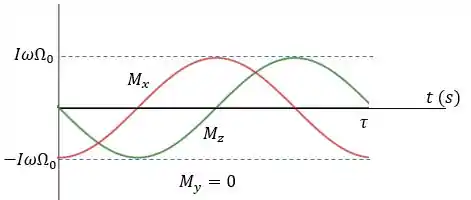
Gráfico da variação dos torques em função do tempo:

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

100. O ventilador para uma aplicação especial é montado conforme mostrado. O rotor do motor, o eixo e as pás têm uma massa combinada de 2,2k g com raio de giração de 60m m . A posição axial b do bloco
104. Um pequeno compressor de ar para a cabine de um avião é composto pela turbina A de 3,50k g , que aciona o soprador B de 2,40k g a uma velocidade de 20000r p m . O eixo do conjunto está montado tr
Determine o momento de inércia da pirâmide homogênea de massa m em relação ao eixo z . A densidade do material é ρ . Sugestão: utilize um elemento de placa retangular tendo um volume d V = 2 x 2 y d z
O disco de 20 kg A é fixado ao bloco B de 10 kg utilizando o sistema de cabo e polia mostrados. Se o disco rola sem deslizar, determine sua aceleração angular e a aceleração do bloco quando eles são s
A montagem consiste em uma disco de 8 kg e uma barra de 10 kg que está conectada ao disco por um pino. Se o sistema é solto do repouso, determine a aceleração angular do disco. Os coeficientes de atri