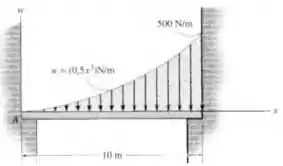
A ação do vento criou um depósito de areia sobre uma plataforma tal que a intensidade da carga de areia sobre essa plataforma pode ser aproximada por uma função . Reduza esse carregamento distribuído a uma força resultante equivalente e especifique a intensidade e a localização da força, medida a partir de .
Passo 1
Iae, meus queridos! Está com dificuldades nessa questão? Não se preocupe! Estamos aqui para ajudar 😉

Sobre uma plataforma de comprimento partindo de , a carga distribuída de areia varia segundo (N/m), com em metros medidos a partir de . Reduzir esse carregamento a uma força resultante equivalente: calcular a intensidade e a posição medida a partir de .
Como vamos resolver isso?
Vamos integrar a intensidade ao longo do comprimento para achar a força resultante.Depois calculamos o momento da distribuição em relação a e dividimos por para obter a posição da resultante.Usamos fórmulas de integração simples porque é dada analiticamente.
Os conceitos e fórmulas que temos que lembrar são:
- A força resultante de uma carga distribuída em é
- A coordenada da linha de ação (centroide da carga) é
Bora lá!
Passo 2
Vamos primeiro calcular a força resultante .
Como a carga varia com , a força total é a integral de de a . Escrevemos então
Integramos usando a regra da potência: .
Assim,
Portanto a intensidade da força equivalente é .
Agora determinamos a posição da força resultante medida a partir de .
Precisamos do primeiro momento da carga em relação a :
Integramos pelo mesmo método:
Então o centroide é
A carga distribuída sobre é equivalente a uma força resultante de intensidade aplicada a de .
É isso, espero ter ajudado! Entendeu tudo? Responde Aí! 😎👍