Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - J. L. Meriam - Estática - Mecânica para Engenharia- Ed: 7º - Capítulo 5.Problemas - Ex. 32

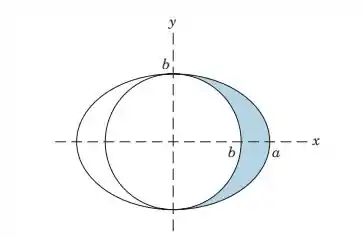
5.32. Locate the centroid of the shaded area between the ellipse and the circle.

Passo 1

Vamos para mais um problema. Nesse aqui nós temos duas funções, um círculo e uma elipse.

A função do círculo é dada por

x 2 + y 2 = b 2

Então

x 2 = b 2 - y 2

x = b 2 - y 2

E a função da elipse é

x 2 a 2 + y 2 b 2 = 1

Vamos isolar x

x 2 a 2 = 1 - y 2 b 2

Então

x 2 a 2 = b 2 - y 2 b 2

x 2 = a 2 b 2 - y 2 b 2

Ficamos com

x = a b b 2 - y 2

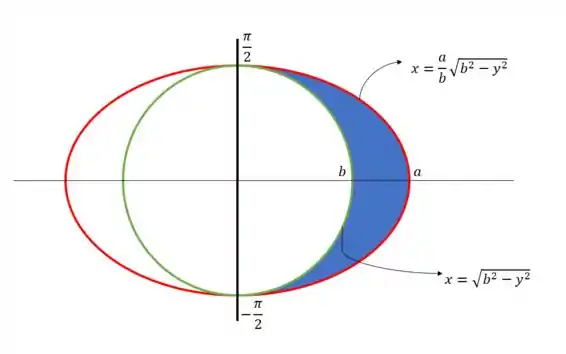
Isso quer dizer que

b 2 - y 2 ≤ x ≤ a b b 2 - y 2

E os limites de y são

- b ≤ y ≤ b

Passo 2

Agora vamos calcular a área da parte pintada da figura. Bom, para fazer isso podemos calcular a área da elipse e subtrair desse valor a área do círculo, e como só a parte da direita está pintada, nós dividimos por dois. Vamos começar coma área da elipse:

A e = a b π

E a área do círculo é

A c = π b 2

Então a área que procuramos é

A = a b π - π b 2 2 = b π a - b 2

Passo 3

Vamos finalmente montar nossa integral

x C = 1 A ∫ - b b ∫ b 2 - y 2 a b b 2 - y 2 x   d x d y

Vamos começar a resolver nossa integral.

x C = 1 A ∫ - b b x 2 2 b 2 - y 2 a b b 2 - y 2 d y

Então

x C = 1 2 A ∫ - b b a 2 b 2 b 2 - y 2 - b 2 - y 2   d y

Colocamos b 2 - y 2 em evidência

x C = 1 2 A ∫ - b b b 2 - y 2 a 2 b 2 - 1   d y

Ou seja

x C = 1 2 A ∫ - b b b 2 - y 2 a 2 - b 2 b 2   d y

Olha só que interessante, o termo a 2 - b 2 b 2 é constante, então podemos tirar da integral.

x C = 1 2 A a 2 - b 2 b 2 ∫ - b b b 2 - y 2   d y

Vamos continuar com a integral

x C = 1 2 A a 2 - b 2 b 2 b 2 y - y 3 3 - b b

Aplicando os limites

x C = 1 2 A a 2 - b 2 b 2 b 2 b - b 3 3 - b 2 - b - - b 3 3

Então

x C = 1 2 A a 2 - b 2 b 2 2 3 b 3 - - 2 3 b 3

Logo

x C = 1 2 A a 2 - b 2 b 2 4 3 b 3

Vamos simplificar b

x C = 1 2 A a 2 - b 2 4 3 b

Passo 4

Substituindo o valor da área na equação ficamos com

x C = 1 2 b π a - b 2 a 2 - b 2 4 3 b

Isso fica

x C = a 2 - b 2 4 b 3 b π a - b

Podemos cortar b

x C = 4 a 2 - b 2 3 π a - b

Vamos usar a igualdade

a 2 - b 2 = a + b a - b

Então

x C = 4 a + b a - b 3 π a - b

E finalmente chegamos em

x C = 4 a + b 3 π

Resposta

x C = 4 a + b 3 π

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Localize o centroide y ¯ da área.
Localize o centroide x ¯ da área.
Localize o centroide y ¯ da área sombreada.
Localize o centroide y ¯ da área sombreada.
Localize o centroide x ¯ da área sombreada.