Enunciado
Física - Mecânica para Engenharia: Dinâmica Volume 2 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 8.5 - Ex. 115
Cada uma das duas barras esbeltas uniformes de 1,5 kg é articulada livremente em A, com seu pequeno rolete de guia, na extremidade superior, livre para se deslocar na guia horizontal. As barras são sustentadas em suas posições de equilíbrio a pela mola vertical com rigidez 105 N/m. Se o ponto A recebe um deslocamento vertical muito pequeno e em seguida é solto, calcule a frequência natural do movimento resultante.
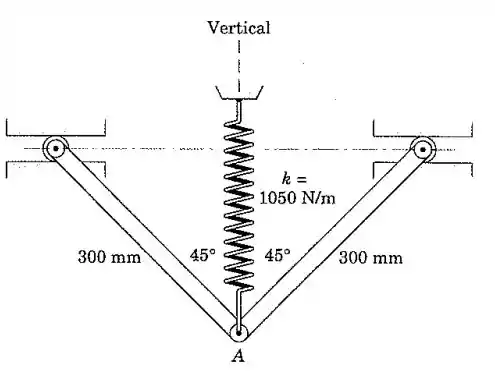
Passo 1
Bom pessoal, o conceito do centro instantâneo de velocidade nula vai nos ajudar a tornar mais esta questão mais simples. Vejamos a figura com uma barra:
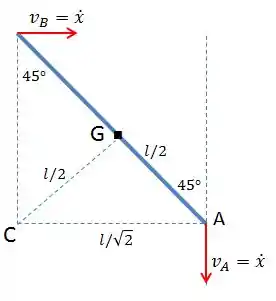
No mecanismo, o ponto A se desloca na vertical e o ponto B está restrito ao movimento horizontal. Traçando perpendiculares aos vetores velocidades, encontramos o centro instantâneo C. Associado aos ângulos de 45 graus, vale a igualdade .
Se considerarmos que o deslocamento do ponto A foi de , a velocidade neste ponto é a sua derivada Deste modo, a velocidade angular é dada por:
Agora, podemos calcular a energia cinética do sistema em relação ao eixo C. Com o auxilio da figura acima e usando o teorema dos eixos paralelos, temos que:
Agora vamos para o cálculo da energia.
A energia cinética no ponto C é composta apenas pela componente rotacional , pois o centro instantâneo possui velocidade nula
Como são 2 barras, a energia cinética será a soma das duas.
Passo 2
Agora vamos para a parte de energia potencial.
A energia potencial do sistema é igual soma das variações da energia potencial elástica e da gravitacional.
Lembrando sempre que no equilíbrio a mola está estendida de, devido ao peso das barras.
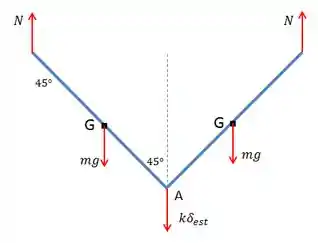
Pela equação de equilíbrio:
Pela simetria: , então
Agora voltando para o calculo da energia, quando a mola é esticada um para baixo:
Agora, vamos para a equação de energia total do sistema. Basta juntar as equações (1) e (2):
Como o sistema é conservativo, (Não esquecer a regra da cadeira):
Agora temos uma equação nos moldes da equação do movimento harmônico. Com isto, sabemos a frequência natural:
Podemos relacionar a frequência à velocidade angular:
Substituindo na equação, temos que: