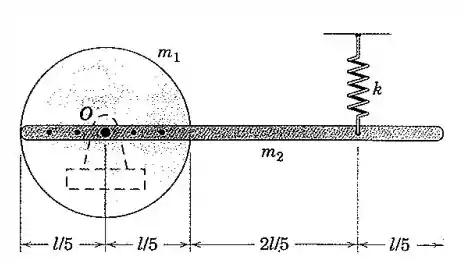
A haste esbelta uniforme de comprimento e massa está fixada ao disco uniforme de raio e massa . Se o sistema é apresentado em sua posição de equilíbrio, determine a frequência natural e a velocidade angular máxima para pequenas oscilações de amplitude em torno do eixo O.

Bom pessoal, como o enunciado pede a amplitude em torno do eixo O, vamos usar este ponto como sendo o centro de nosso sistema. Então, podemos calcular o momento de inercia da marra no eixo O usando o teorema dos eixos paralelos. Veja o diagrama:

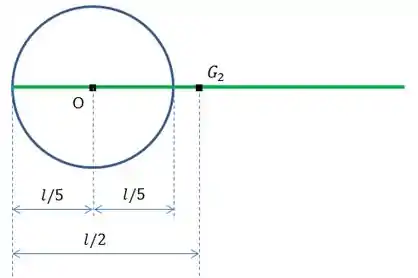
Então, o momento de inércia em relação ao eixo O pode ser escrito como:

O momento de inércia de um disco vale:

O momento de inércia de uma barra vale:

Portanto, substituindo na equação acima:

Agora vamos para a parte de energia.

Como sabemos, em um movimento harmônico simples, a energia é um balanço entre a energia cinética e a energia potencial, como mostra a equação:

Como o sistema é conservativo, a energia total E é uma constante. Além disso, nós temos que quando a energia cinética é máxima, a energia potencial é nula, e vice versa. Veja só:

Podemos considerar que neste instante, quando , a mola está no seu comprimento natural. Ou seja, a energia potencial elástica é nula.

Agora, vamos voltar para a equação do movimento harmônico e escrever de uma maneira mais completa de acordo com a questão.

Onde a energia cinética é composta apenas pela energia cinética rotacional , pois o eixo O não possui velocidade.

A equação da energia cinética fica assim:

Agora, para analisar a energia potencial elástica, vamos supor uma oscilação de no sistema. Veja como fica o diagrama:

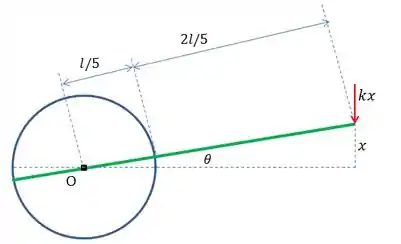
No instante representado acima, a deflexão da mola vale . Mas para pequenos ângulos, vale a aproximação:

Então temos que:

A energia potencial elástica fica da seguinte forma:

Agora podemos substituir os valores na equação da energia:

Como o sistema é conservativo, (Não esquecer a regra da cadeira):

Arrumando a equação para o termo a segunda ficar com o coeficiente unitário, temos:

Agora temos uma equação nos moldes da equação do movimento harmônico. Com isto, sabemos a frequência natural:

Para encontrar a velocidade angular máxima, vamos partir da equação da solução geral:

Derivando:

Para a velocidade angular ser máxima, o cosseno deve ser o maior possível :