Cada um dos parafusos de aço e () tem um diâmetro de e tem suas extremidades superiores rosqueadas, com rosca simples e de passo igual a . Sabendo-se que a porca em , depois de ser perfeitamente ajustada, é apertada de duas voltas completas, determinar: (a) a tração em cada barra; (b) a deflexão no ponto da barra rígida .
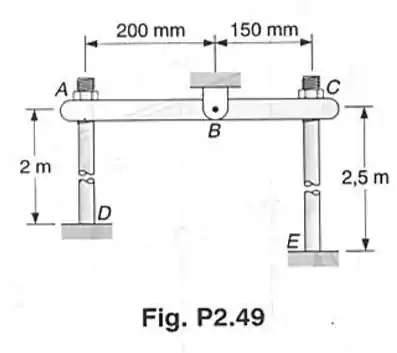
Passo 1
Vamos entender o que está se passando aqui. Quando o problema fala que a rosca está perfeitamente ajustada isso significa que, inicialmente, não há deformação nas barras. Mas logo depois a rosca é apertada, isso faz com que o parafuso sofra uma deformação e, além disso, apareçam diversas forças no nosso sistema.
Então para resolver vamos seguir a receita de bolo deste tipo de exercício que é basicamente:
- Fazer o diagrama de corpo livre.
- Achar uma equação que relacione as forças.
- Analisar a geometria da figura.
- Aplicar as equações de deflexão.
- Correlacionar as forças com as deflexões.
Passo 2
Então vamos fazer o diagrama de corpo livre da barra .
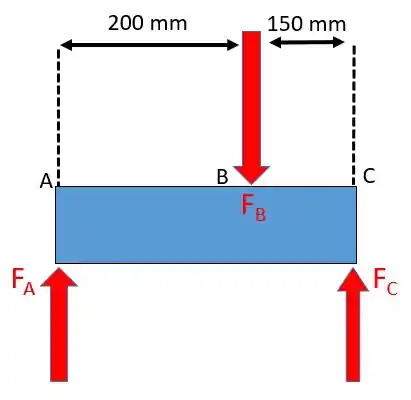
Como a força no ponto não nos interesse e nem nos foi dada então vamos aplicar o momento no ponto :
Considerando o sentido horário positivo
Passo 3
Agora vamos analisar a geometria dessa figura.
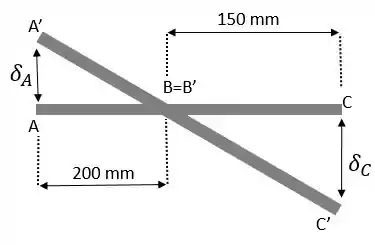
Com o aperto do parafuso o ponto deslocou-se para o ponto e o ponto para o ponto enquanto o ponto permanece no mesmo lugar pois está fixo, sendo assim igual a .
Com isso os dois triângulos e são semelhantes (olha o ângulo oposto pelo vértice e o ângulo reto).
Então podemos achar a seguinte relação:
Passo 4
Mas agora observa só uma coisa, o parafuso de não foi mexido, logo, a deflexão de é igual a:
Onde a área é igual a
Show de bola mas e a deflexão de ? Pela geometria a gente já sabe que vai dar
Mas e pela fórmula? Ótimo pergunta jovem gafanhoto!
Infelizmente, neste caso, a fórmula não vai nos dar o resultado correto, isso porque não considera o aperto do parafuso.
Como o parafuso gira duas voltas com um passo de então o avanço vai ser de
Mas ao mesmo tempo que o parafuso avança, a barra é comprimida e essa compressão deve ser considerada na deflexão. Assim a deflexão de vai ser, na verdade um pouquinho menor do que 4 sendo igual a:
Passo 5
Agora temos as seguintes equações:
4 equações e 4 incógnitas, a partir de agora é pura álgebra =) ou =( kkk
Vamos lá! Na letra A o problema pede a tração em cada barra, ou seja, e .
Das duas equações
Vamos substituir na primeira equação
Como
Vamos ter
E como
Acabamos com
E
Passo 6
Para achar a deflexão basta substituir em
Resposta
a)
b)