Enunciado
Mecânica e Resistência dos Materiais - Hibbeler - Estática- Ed: 14º - Capítulo 3.Problemas Fundamentais - Ex. 11
A caixa de é sustentada pelos cabos AB, AC e AD. Determine a tração nesses cabos.
Passo 1
Oi pessoal? Vamos para mais um exercício?
Montando o diagrama de corpo livre:
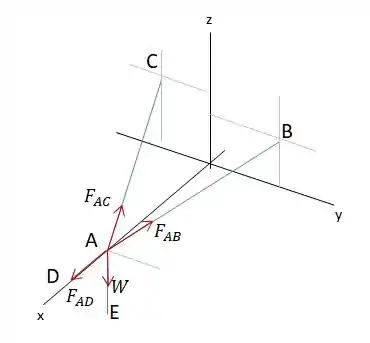
Para que o sistema esteja em equilíbrio, temos que:
Sabemos que o vetor força é dado pelo produto entre a intensidade da força e o vetor direção unitário relacionado a ele.
Temos que:
Passo 2
Agora podemos encontrar o vetor força de cada elemento:
Para , temos:
E para , temos:
Passo 3
Como dito anteriormente, nossa condição de equilíbrio é de que:
Portanto:
Rearranjando, temos que:
Temos então equações:
Como , temos 3 equações e 3 incógnitas.
Fazendo um sistema com essas equações temos que:
Resposta
Exercícios de Livros Relacionados
94- Duas correias de transmissão passam por duas roldanas soldadas a um eixo apoiado por mancais em B e D . A roldana em A tem um raio de 60m m , e a roldana em C tem um raio de 50m m . Sabendo que o
118- Resolva o Problema 4.117 , considerando que o cabo E F é substituído por um cabo preso aos pontos E e H .
95- Uma alavanca de 200m m e uma polia de diâmetro de 240m m estão soldadas ao eixo B E que é suportado pelos mancais em C e D . Se a carga vertical de 720N é aplicada em A quando a alavanca está na h
117- A placa retangular mostrada na figura tem peso de 300N e é mantida na posição mostrada pelas dobradiças A e B e pelo cabo E F . Considerando que a dobradiça em B não exerce qualquer esforço axial
119- Resolva o Problema 4.114 , considerando que o mancal em D é removido e que o em C pode exercer binários em relação aos eixos y e z .