Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Estática- Ed: 9º - Capítulo 5.Problemas - Ex. 40

Determine as coordenadas do centroide por integração em termos de a e b :

Passo 1

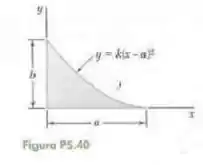
Fala aí galera, vamos para mais um problema de estática. O primeiro passo é determinar a relação entre x   e y . Neste caso:

y = k x - a 2

Logo, pegando-se um elemento retangular infinitesimal, teremos que:

d A = y d x

Agora, vamos utilizar a fórmula abaixo:

x - = ∫ x d A ∫ d A  

Logo:

x - = ∫ x d A ∫ d A   = ∫ 0 a k x x - a 2 d x ∫ 0 a y d x = ∫ 0 a k x 3 - 2 k x 2 a + k x a 2 d x ∫ 0 a ( k x 2 - 2 k x a + k a 2 ) d x = k a 4 4 - 2 k a 4 3 + k a 4 2 k a 3 3 - 2 k a 3 2 + k a 3

x - = k a 4 12 k a 3 3 = a 4

Para a coordenada y :

y - = ∫ y 2 d A ∫ d A   = ∫ 0 a y 2 2 d x ∫ 0 a y d x = ∫ 0 a 1 2 k ² x 4 - 4 k ² a x 3 + 6 k 2 a 2 x 2 - 4 a 3 x k ² + a 4 k ² d x ∫ 0 a k x 2 - 2 k x a + k a 2 d x

y - = 1 2 ( k 2 a 5 5 - 4 k 2 a 5 4 + 6 k 2 a 5 3 - 4 k 2 a 5 2 + a 5 k ) k a 3 3 - 2 k a 3 2 + k a 3 = k ² a 5 10 k a 3 3 = 3 k a 2 10

Como o problema nos pede em função e a   e b ,   temos que substituir o k .   Sabemos que:

k = b a 2

Logo:

y - = 3 a 2 10 × b a 2 = 3 b 10

Resposta

x - = a 4

y - = 3 b 10

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

87- Uma casca fina, mostrada em seção, tem sua forma gerada pela revolução do arco por 360 em torno do eixo z . Determine a área superficial A de um dos dois lados da casca.
94- Para dar sustentação suficiente para o arco de blocos de pedra projetado como mostrado, é necessário conhecer seu peso total W . Use os resultados do Prob. 5 / 11 e determine W . A massa específic
93- Calcule a massa m de concreto necessária para construir a represa em arco mostrada. O concreto tem uma massa específica de 2.4M g / m 3
92- Ache o volume V do sólido gerado pela revolução da área sombreada por 90 gruas em torno do eixo x
A área de um setor circular é girada de 180° em torno do eixo y. Determine o volume do corpo resultante, o qual é parte de uma esfera.