Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Estática- Ed: 9º - Capítulo 8.Problemas - Ex. 41

Duas barras idênticas de 1,5 m de comprimento conectadas por um pino em B estão colocadas entre duas paredes e uma superfície horizontal como mostrado na figur. Designando por μ s o coeficiente de atrito estático em A, B e C, determine o menor valor de μ s para que o equilíbrio seja mantido.

Passo 1

Tá legal! Vamos começar esse excercício assumindo uma tendência de movimento no sentido anti-horário, desenhando o DCL para a barra da esquerda:

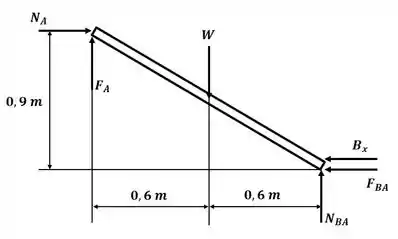
Sabemos que as forças de atrito podem ser calculadas por:

F B A = μ s N B A

F A = μ s N A

Agora, aplicando o somatório de momento em relação ao ponto B:

+ ↺ ∑ M B = 0

0,6 W - 0,9 N A - 1,2 μ s N A = 0 → N A = 0,6 W 1,2 μ s + 0,9

Essa será nossa equação 1. Agora podemos aplicar o somatório de forças na direção y :

+ ↑ ∑ F y = 0

N A B - W + μ s N A = 0 → N A B = W - μ s N A

Essa será nossa equação 2. Agora aplicando o somatório de forças na direção x :

+ → ∑ F x = 0

- B x - μ s N B A + N A = 0 → B x = N A - μ s N B A

Essa será nossa equação 3.

Passo 2

Agora vamos desenhar o diagrama de corpo livre para a barra da direita:

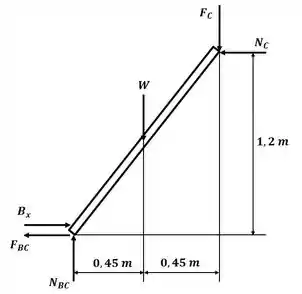
Sabemos que as forças de atrito podem ser calculadas por:

F B C = μ s N B C = μ s N B C

F C = μ s N C

Agora, aplicando o somatório de momento em relação ao ponto B:

+ ↻ ∑ M B = 0

0,45 W - 1,2 N C + 0,9 μ s N C = 0 → N C = 0,45 W 1,2 - 0,9 μ s

Essa será nossa equação 4. Agora podemos aplicar o somatório de forças na direção y :

+ ↑ ∑ F y = 0

N B C - W - μ s N C = 0 → N B C = W + μ s N C

Essa será nossa equação 5. Agora aplicando o somatório de forças na direção x :

+ → ∑ F x = 0

B x - N C - μ s N B C = 0 → B x = N C + μ s N B C

Essa será nossa equação 6.

Passo 3

Agora vamos resolver o sistema de equações encontrado, começando igualando as equações 5 e 6:

N A - μ s N B A = N C + μ s N B C

Agora vamos substituir os valores encontrados para N B A na equação 2 e N B C na equação 5:

N A - μ s W - μ s N A = N C + μ s W + μ s N C

N A 1 + μ s 2 - μ s W = N C 1 + μ s 2 + μ s W

Agora vamos substituir os valores encontrados para N A e N C :

0,6 W 1,2 μ s + 0,9 1 + μ s 2 - μ s W = 0,45 W 1,2 - 0,9 μ s 1 + μ s 2 + μ s W

0,6 + 0,6 μ s 2 1,2 μ s + 0,9 - μ s = 0,45 + 0,45 μ s 2 1,2 - 0,9 μ s + μ s

Resolvendo essa equação com a ajuda de uma calculadora, temos:

μ s = 0,0949

Resposta

μ s = 0,0949

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Determine a força P mínima que pode ser aplicada sem causar o movimento da caixa de 125k g com centro de gravidade em G . O coeficiente de atrito estático no piso é μ s = 0,4 .
Determine a força P mínima para impedir que a barra A B de 30 k g deslize. A superfície de contato em B é lisa, enquanto o coeficiente de atrito estático entre a barra e a parede em A é μ s = 0,2 .
Se cada caixa pesa 75k g , determine a menor força horizontal P que o homem precisa exercer na caixa de cima a fim de causar movimento. O coeficiente de atrito estático entre as caixas é μ s = 0,5 , e
O carpinteiro empurra lentamente a tábua uniforme horizontalmente sobre o topo do cavalete. A tábua tem um peso uniforme de 50N / m , e o cavalete tem um peso de 75N e centro de gravidade em G . Deter
O carpinteiro empurra lentamente a tábua uniforme horizontalmente sobre o topo do cavalete. A tábua tem um peso uniforme de 50N / m , e o cavalete tem um peso de 75N e centro de gravidade em G . Deter