Enunciado
Mecânica e Resistência dos Materiais - Beer - Estática- Ed: 9º - Capítulo 8.Problemas - Ex. 50
A elevação da extremidade de uma viga de aço apoiada em um piso de concreto é ajustada através das cunhas de aço E e F. A placa de base CD foi soldada no flange inferior da viga e sabe-se que a reação na extremidade da viga é 100 kN. O coeficiente de atrito estático é 0,30 entre as duas superfícies de aço e 0,60 entre o aço e o concreto. Se o movimento horizontal da viga é contido pela força Q, determine a força P necessária para se erguer a viga, a força Q correspondente.
Passo 1
Tá legal! Vamos começar esse excercício desenhando o diagrama de corpo livre para a viga:
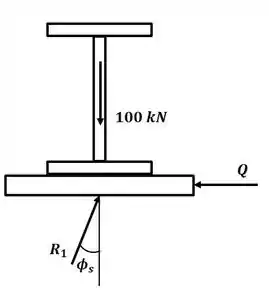
Conforme vimos na seção anterior do livro, o coeficiente de atrito pode ser encontrado através de:
Substituindo o valor dado de :
Passo 2
Agora, podemos desenhar o triângulo de forças para o sistema anterior:
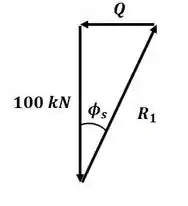
Por trigonometria, podemos encontrar o valor de
Passo 3
Agora vamos analisar o desenhar o diagrama de corpo livre para a cunha E:
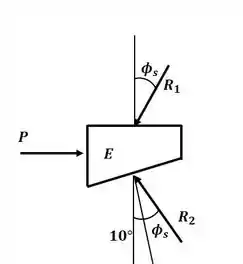
E, com esse DCL, podemos montar o triângulo de forças a seguir:
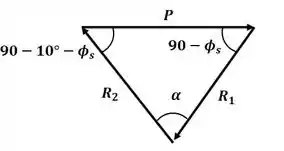
Podemos descobrir o valor de através da soma dos ângulos internos do triângulo:
Agora vamos aplicar a lei dos senos para esse triângulo:
E, para esse valor de , se retornarmos ao triângulo de forças do passo 2, podemos escrever: