Enunciado
Mecânica e Resistência dos Materiais - J. L. Meriam - Estática - Mecânica para Engenharia- Ed: 7º - Capítulo 4.Problemas - Ex. 61
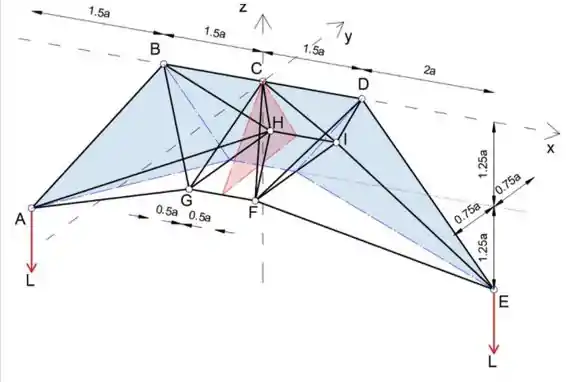
A estrutura representada está sendo considerada como a parte superior de uma torre de linha de transmissão e é apoiada nos pontos F, G, H e I. O ponto C está diretamente acima do centro do retângulo FGHI. Determine a força no membro CD.
Passo 1
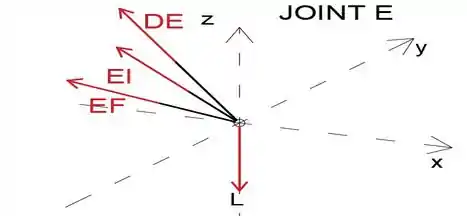
A fim de determinar a força no membro CD, primeiro determinaremos a força DE analisando a junta E, depois disso, haverá três forças desconhecidas agindo em D, então, analisando a junta D, podemos determinar a força CD A intersecção da treliça com o plano de Oz da te é pintada em vermelho e a intersecção da treliça com o plano xOz em azul para facilitar a leitura das coordenadas dos pontos. Vamos supor que todos os membros estão em tensão. Podemos escrever as forças L como vetores
Podemos escrever o vetor de força EF como um produto de sua magnitude EF e um vetor unitário de direção de força
Podemos ver na imagem que as coordenadas dos pontos E e F são
Visto que conhecemos dois pontos de ação, podemos escrever
Podemos escrever o vetor de força como um produto de sua magnitude EI e um vetor unitário de direção de força nEI
Podemos ver da figura que as coordenadas do ponto E e I
Uma vez que conhecemos os dois pontos de ação, podemos escrever como
Passo 2
Podemos escrever o vetor de força como um produto de sua magnitude DE e um vetor unitário de direção de força nDE
Podemos ver da figura que as coordenadas do ponto E e D
Uma vez que conhecemos os dois pontos de ação, podemos escrever como
Agora que escrevemos todas as forças como vetores, podemos escrever três equações de equilíbrio, igualando a soma das forças agindo no ponto E a zero
Agora temos 3 equações de equilíbrio
(1)
(2)
(3)
Multiplique equação (1) por
(4)
Agora podemos adicionar (3) e (4) para obter a equação onde a força DE será a única incógnita
Agora que determinamos a força DE, analisando a junta D, podemos determinar a força na barra CD
Uma vez que o CD membro é paralelo ao eixo x, podemos escrevê-lo como
Podemos escrever o vetor de força como um produto de sua magnitude DF e um vetor unitário de direção de força nDF
Podemos ver na figura os pontos de coordenadas D e F
Uma vez que conhecemos os dois pontos de ação, podemos escrever como
]
Passo 3
Podemos escrever o vetor de força como um produto de sua magnitude DI e um vetor unitário de direção de força nDI
Podemos ver na figura os pontos de coordenadas D e I
Uma vez que conhecemos os dois pontos de ação, podemos escrever como
Agora que escrevemos todas as forças como vetores, podemos escrever três equações de equilíbrio igualando a soma das forças a zero
Observe que a força DE mudou de direção, então agora seu vetor é
Agora temos 3 equações de equilíbrio
(5)
(6)
(7)
Passo 4
Da equação (6), podemos ver que as forças DF e DI são iguais
Em seguida, substituindo DF por DI na equação (7), podemos determinar seu valor, uma vez que já sabemos a magnitude da força DE
(7)
Finalmente, colocando os valores de DE, DF e DE na equação (5), podemos determinar a força no membro CD