Uma força P de 700 N é aplicada no ponto A de um elemento estrutural. Substitua P por um sistema força-binário equivalente em C e um sistema equivalente que consista em uma força vertical em B e uma segunda força em D.
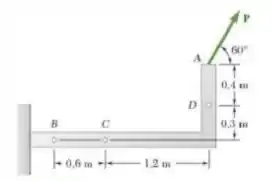
Passo 1
Falaaa... beleza??? Vamos matar essa questão?
Aqui a gente vai precisar substituir uma força por um sistema binário em C.
E depooooiss substituir por um sistema com uma força vertical em B e uma outra força em D.
Passo 2
a) Para o binário em C. Só precisamos lembrar que a força do binário em C é igual à força original e o vetor binário é igual ao momento da força original em relação ao ponto C.
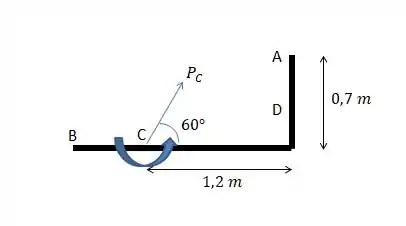
- Pra força:
- Para o vetor binário:
Passo 3
b) Agora é pra trocar por duas forças, uma vertical em B e outra força em D, que não sabemos o ângulo.
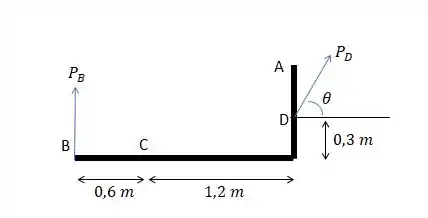
Daí ficamos com: (em x)
E calculando momento em D: (do P de antes e das duas forças)
Fazendo o somatório de forças em y:
Então já podemos achar , mandando um teorema de pitágoras:
Só falta o ângulo, heim:
Então: