Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Dinâmica Volume 2 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 5.7 - Ex. 178

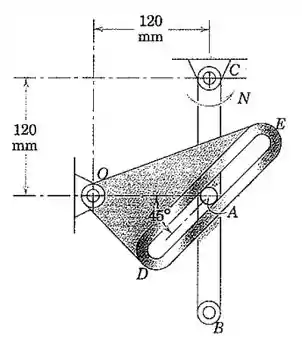
Para o instante representado, a barra CB está girando no sentido anti-horário a uma taxa constante N = 4   r a d / s , e seu pino A provoca uma rotação sentido horário do membro ranhurado ODE. Determine a velocidade angular ω e a aceleração angular α de ODE para esse instante.

Passo 1

Fala galera, vamos começar fazendo um esboço do mecanismo para melhor visualização do seu funcionamento.

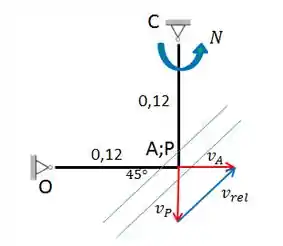
Agora, vamos interpretar o mecanismo e suas velocidades. Bom, em exercícios que possuem ranhura e deslizamento, costumamos considerar um ponto coincidente com A que seja pertencente ao elemento ranhurado. Simplificando, temos um ponto A que pertence à barra CB e um ponto P que pertence ao ranhurado ODE, e neste instante os dois estão localizados no mesmo lugar (está um em cima do outro).

Beleza! Então podemos calcular as velocidades de A e P individualmente. Vamos fazer isso:

v A = N × A C - = 4 k ^ × - 0,12 j ^ = 0,48 i ^   m / s

v P = ω k ^ × P O - = ω k ^ × 0,12 i ^ = 0,12 ω j ^   m / s

Bom, olhando para a figura do sistema de modo geral, vemos que o pino A só pode se locomover dentro da ranhura. Ou seja, a velocidade relativa entre A e P deve estar na direção da ranhura.

v r e l = v A s e n 45 = 0,48 2   m / s

Por Pitágoras, relacionamos as velocidades:

v A 2 + v P 2 = v r e l 2

0,48 2 + 0,12 ω 2 = 0,48 2 2

ω = 4 r a d s ,   s e n t i d o   h o r á r i o

Passo 2

Agora, vamos para o cálculo das acelerações.

Podemos calcular a aceleração de A a partir da barra CA. Pelo enunciado, N é constante, então não terá componente tangencial, apenas normal.

a A = - r A C N 2 = - - 0,12 j ^ 4 2 = 1,92 j ^   m / s 2

De mesma forma, faremos para o ponto P a partir de PO. Porém, queremos saber sua componente tangencial α . Vamos lá:

a P = - r P O ω 2 + α × r P O = - 0,12 i ^ 4 2 + α k ^ × 0,12 i ^

a P = - 1,92 i ^ + 0,12 α j ^   m / s 2

Agora, vamos usar a equação da aceleração relativa aprendida nesta seção entre os pontos A e P:

a A = a P + α A P × r A P + ω A P × ω A P × r A P + 2 ω × v r e l + a r e l

Como A e P são coincidentes r A P = 0 :

a A = a P + 2 ω × v r e l + a r e l

E podemos substituir os valores:

1,92 j ^ = - 1,92 i ^ + 0,12 α j ^ + 2 - 4 k ^ × 0,48 2 i ^ s e n 45 ° + j ^ c o s 45 ° + a r e l

1,92 j ^ = - 1,92 i ^ + 0,12 α j ^ + 3,84 i ^ - 3,84 j ^ + a r e l

A a r e l do sistema, seguindo a mesma linha da v r e l está na direção da ranhura, isto é:

a r e l = a r e l i ^ s e n 45 ° + j ^ c o s 45 °

Decompondo nas direções:

0 = - 1,92 i ^ + 3,84 i ^ + 2 2 a r e l i ^

1,92 j ^ = + 0,12 α j ^ - 3,84 j ^ + 2 2 a r e l j ^

Resolvendo o sistema, temos que:

a r e l = 2,72   m / s 2

α = 64 k ^   r a d / s 2

Resposta

ω = 4 r a d s ,   s e n t i d o   h o r á r i o

α = 64 k ^   r a d / s 2

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Se o anel A se desloca com uma velocidade constante v A = { 3 i } m / s , determine a velocidade do anel B quando a barra AB está na posição mostrada. Suponha que a velocidade angular de AB é perpendi
A manivela AO gira no sentido horário com uma velocidade angular constante de 10 rad/s dentro de um arco limitado de seu movimento. Para a posição θ = 30 ° determine a velocidade angular da barra ranh
O ônibus espacial A está em uma órbita circular equatorial de 240 km de altitude e está se movendo de oeste para leste. Determine a velocidade e a aceleração que ele parece ter para um observador B fi
Determine a aceleração angular da haste EC na posição mostrada, onde ω = β ˙ = 2 r a d seβ ¨ = 6r a d / s 2 quando θ = β = 60 ° . O pino A é fixo na haste EC. A ranhura circular no elemento DO tem um
Dois satélites estão em orbitas circulares equatoriais de diferentes altitudes. O satélite A está em uma órbita geossíncrona (uma com o mesmo período que o da rotação da Terra, de modo que ele “paira”