Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Estática Volume 1 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 6.7 - Ex. 92
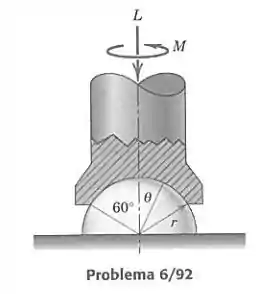
Um mancal radial para um eixo sob uma carga axial é projetado como um copo esférico parcial de raio . Se a pressão entre as superfícies do mancal em qualquer ponto varia de acordo com , deduza a expressão para o torque requerido para manter uma velocidade de rotação constante. O coeficiente de atrito é .
Passo 1
Para resolver esse exercício, precisamos achar a expressão do momento infinitesimal feito pelo atrito em cada parte da superfície de contato esférica, e então integrar. O momento total será o momento necessário para vencer o atrito e fazer o mancal girar. Vamos dividir nossa superfície em círculos horizontais, definidos pelo ângulo , que vai de a . Cada círculo terá uma área dada pela circunferência do círculo vezes o comprimento infinitesimal de um arco:
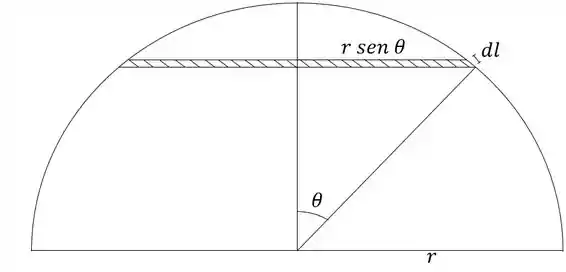
A área de cada círculo é:
Passo 2
Em cada círculo, atua uma força normal , que é a pressão vezes a área.
O atrito será a força normal vezes o coeficiente de atrito, e o momento em torno do centro feito por cada força é vezes a distância até o eixo central, que é :
Agora substituímos :
Para resolvermos a integral, precisamos antes do valor de , e acharemos esse valor através do cálculo da força vertical total sobre a superfície.
Passo 3
A força será igual a todas as componentes verticais das forças normais aplicadas na superfície. A componente vertical de cada força é , então devemos integrar :
Já calculamos em função de :
Então:
Calculando a integral, achamos a relação entre e :
Passo 4
Agora vamos substituir na expressão de :
Pronto, agora devemos integrar de a :