Um motorista que dirige ao longo de um trecho de reta de uma rodovia diminui a velocidade de seu automóvel para uma taxa constante antes de sair da rodovia em direção a uma rampa de saída circular com um raio de 168 m. Ele continua a desaceleração com a mesma taxa constante de tal forma que, 10 s após ter entrado na rampa, sua velocidade escalar diminuiu para 32 km/h, uma velocidade escalar que ele, então, mantém. Sabendo que a essa velocidade constante a aceleração total do carro é igual a um quarto de seu valor antes de entrar na rampa, determine o valor máximo da aceleração total do carro.
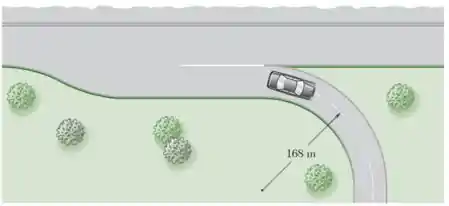
Passo 1
Primeiro note
Enquanto o carro estiver na porção reta da rodovia.
e para a rampa de saida circular
onde
Passo 2
Por observação, ocorre quando v é máximo, que é em t = 0 quando o carro recém entra a rampa.
Para movimento uniformemente desacelerado
e em t = 10 s:
Então
ou
( o carro está desacelerando por isso o sinal de menos.)
Então em t = 10 s:
ou
Então em t = 0: