Exercícios de Movimento Retilíneo - Lista de Exercícios Resolvida
Questão 1
Um veículo entra em uma seção de teste de uma estrada reta em com uma velocidade de . Em seguida sofre uma aceleração que varia com o deslocamento como mostrado na figura. Determine a velocidade do veículo quando este passa pela posição .
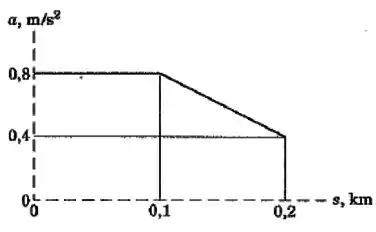
Questão 2
Um avião a jato com uma velocidade de pouso de tem um máximo de de pista disponível após tocar o solo no qual deve reduzir sua velocidade para . Calcule a aceleração média requerida da aeronave durante a frenagem.
Ver solução completaQuestão 3
A aceleração de uma partícula que está se movendo ao longo de uma linha reta é dada por , onde é em metros por segundo ao quadrado, é uma constante, e é a velocidade em metros por segundo. Determine a velocidade como função tanto do tempo como da posição . Avalie suas expressões para e em se e as condições iniciais no instante são e .
Ver solução completaQuestão 4
A posição de uma partícula é dada por , onde é em metros e é em segundos. Represente graficamente a posição, velocidade, e aceleração como funções do tempo para os primeiros segundos de movimento. Determine o instante em que a velocidade é zero.
Ver solução completaQuestão 5
Uma bola é lançada verticalmente para cima com uma velocidade de na borda de um penhasco com . Calcule a altura para a qual a bola se eleva e o tempo total após a liberação para a bola alcançar o fundo do penhasco. Despreze a resistência do ar e considere a aceleração para baixo como .
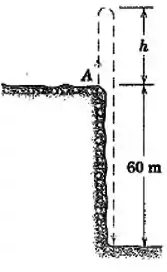
Questão 6
O piloto de um avião de transporte a jato leva os motores a plena potência de decolagem antes de liberar os freios enquanto a aeronave está parada sobre a pista. O empuxo do jato permanece constante, e a aeronave tem uma aceleração quase constante de . Se a velocidade de decolagem é , calcule a distância e o tempo do repouso até a decolagem.
Ver solução completaQuestão 7
A velocidade de uma partícula que se desloca ao longo do eixo é dada por , onde é em segundos e é em metros por segundo. Calcule a posição , a velocidade , e a aceleração quando . A partícula está na posição quando .
Ver solução completaQuestão 8
A resistência aerodinâmica ao movimento de um carro é aproximadamente proporcional ao quadrado da sua velocidade. A resistência adicional ao atrito é constante, de modo que a aceleração do carro quando em ponto morto pode ser escrita , onde e são constantes que dependem da configuração mecânica do carro. Se o carro tem uma velocidade inicial quando o motor é desengrenado, derive uma expressão para a distância necessária para o carro mover-se em ponto morto até parar.
Ver solução completa