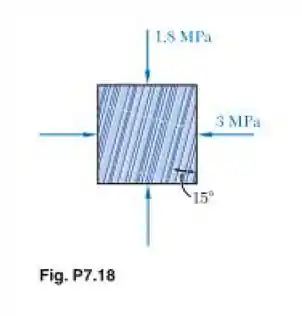
Resolva o Problema 7.18 usando o círculo de Mohr.

Passo 1
Beleza! Através do estado de tensões que foi dado no enunciado, conseguimos esboçar o círculo de Mohr para esse estado. Com o auxílio do círculo, podemos rotacionar o elemento diferencial de 15°, ou seja, andar 30° no círculo para descobrir a localização dos pontos de cisalhamento e tensão normal nas direções pedidas.
Passo 2
Tá legal! Vamos começar calculando a tensão média, que é dada por:
Substituindo os valores conhecidos, teremos:
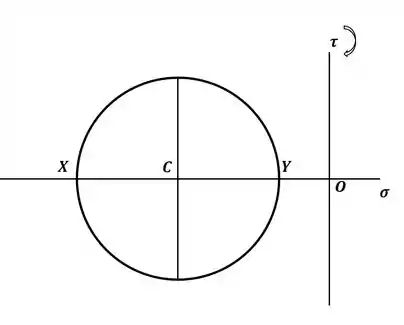
Agora, vamos escrever as coordenadas dos pontos para o círculo de Mohr, no nosso caso, temos:
Então, com esses pontos, temos o seguinte círculo de Mohr:
Passo 3
Com o círculo de Mohr esboçado, podemos encontrar seu raio subtraindo a tensão Y da tensão X e dividindo esse valor por 2, ou seja:
Agora, para a letra (a), precisamos rotacionar o elemento diferencial em 15° para podermos encontrar a tensão de cisalhamento num plano paralelo ao plano das fibras de madeira, sendo assim, rotacionando o elemento em 15°, ou seja, percorrendo 30° no círculo de Mohr, os novos pontos estarão em:
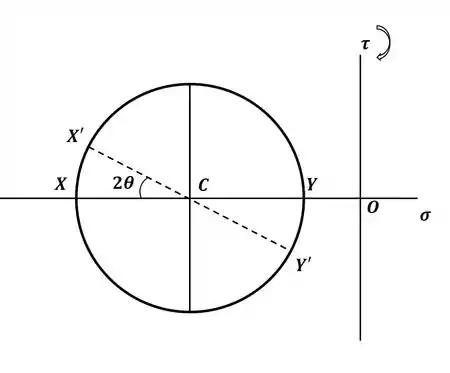
Então, podemos encontrar a tensão de cisalhamento utilizando trigonometria, da seguinte forma:
Substituindo os valores conhecidos, temos:
Passo 4
Agora para a letra (b), resta encontrar a tensão normal perpendicular as fibras, como na letra (a) encontramos a tensão de cisalhamento paralela as fibras, e sabemos que a tensão normal e a de cisalhamento são perpendiculares, basta encontrar a tensão normal para o mesmo ponto encontrado no passo 3. Então, também através de trigonometria, temos:
Substituindo os valores conhecidos, temos:
Feshooow!