Enunciado
Mecânica e Resistência dos Materiais - Beer - Estática- Ed: 9º - Capítulo 8.Problemas - Ex. 47
Resolva o Problema 8.46 considerando que a cunha deve ser movida para direita.
Passo 1
Tá legal! Vamos começar esse excercício desenhando o diagrama de corpo livre para a peça:
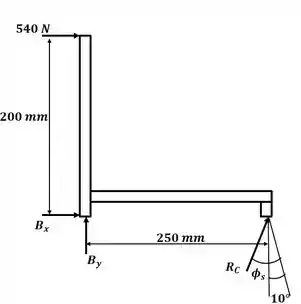
Conforme vimos na seção anterior do livro, o coeficiente de atrito pode ser encontrado através de:
Substituindo o valor dado de :
Agora podemos aplicar o somatório de momento em relação ao ponto B:
Passo 2
Agora vamos analisar o desenhar o diagrama de corpo livre para a cunha:
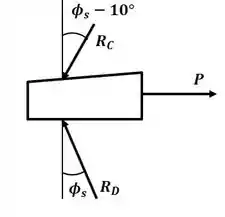
E, com esse DCL, podemos montar o triângulo de forças a seguir:
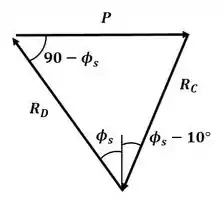
Agora vamos aplicar a lei dos senos para esse triângulo:
Passo 3
Agora vamos voltar a analisar o diagrama de corpo livre da peça ABC apresentado no passo 1. Então, fazendo o somatório de forças na direção :
Agora vamos aplicar o somatório de forças em :
Resposta
Exercícios de Livros Relacionados
53- Um carro de tração traseira com 1600k g está sendo movido para cima da rampa a uma velocidade constante baixa. Determine o mínimo coeficiente de atrito estático μ s para o qual a rampa portátil nã
Se o coeficiente de atrito entre a cunha de aço e as fibras úmidas de um tronco recentemente cortado vale 0,20, deternube i ângulo máximo α que a cunha pode ter para não pular fora da madeira após ter
Os elementos de um tubo de desodorante em barra são mostrados na figura. Para subir a barra do desodorante D , o disco C é girado. O eixo rosqueado se conecta as roscas da base móvel A ; o eixo não te
69- Um macaco sanfona com uma rosca quadrada única, que rosqueia na bucha G e gira em um mancal de rolamentos em D , está sendo projetado. A rosca deve ter um diâmetro de 10m m e um passo (avanço por
124- Uma força compressiva de 600N deve ser aplicada aos dois painéis na garra do grampo C . O parafuso rosqueado tem um diâmetro médio de 10m m e avança 2.5m m por volta. O coeficiente de atrito está