Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Dinâmica Volume 2 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 5.3 - Ex. 32
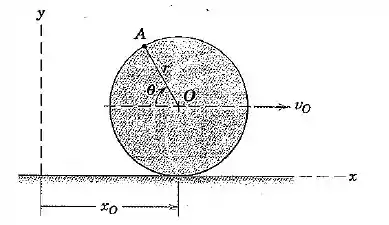
A roda de raio rola sem deslizar, e seu centro possui uma velocidade constante para a direita. Determine expressões para os módulos da velocidade e da aceleração do ponto sobre a borda diferenciando suas coordenadas e . Represente os seus resultados graficamente como vetores em seu esboço e mostre que é a soma vetorial de dois vetores, sendo que cada um possui um módulo .
Passo 1
Vamos escrever as coordenadas do ponto simplesmente olhando para o desenho.
E agora, seguindo a sugestão do enunciado, vamos simplesmente derivar essas coordenadas em relação ao tempo para encontrar a velocidade e a aceleração do ponto.
Para essas derivadas vamos precisar das seguintes relações:
Passo 2
Então começamos derivando a coordenada :
E agora a coordenada :
E então o módulo da velocidade é:
Passo 3
Agora precisamos derivar mais uma vez para encontrar a aceleração. Começando pela velocidade em :
E agora a velocidade em :
E então o módulo da aceleração é:
Passo 4
Agora vamos representar tudo graficamente. Nossos vetores são:
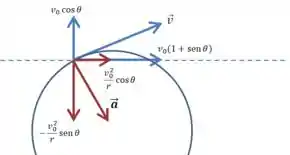
É importante lembrar que, como a velocidade do centro de massa é constante, toda a aceleração do ponto é centrípeta.
Agora falta mostrar que pode ser obtido pela soma vetorial de dois vetores de módulo . Para isso precisamos fazer um desenho:
Para mostrar que essa soma vetorial realmente pode acontecer, vamos ver as componentes e do vetor :
Que é justamente o resultado que encontramos antes!
Resposta
O módulo da velocidade é e o da aceleração é .