Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Resistência dos materiais - 7ª Edição - Russel C. Hibbeler- Ed: 7º - Capítulo 9.Problemas - Ex. 91

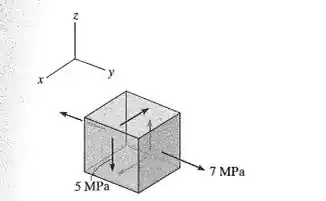
A tensão em um ponto é mostrada no elemento. Determine as tensões principais e a tensão de cisalhamento máxima absoluta.

Passo 1

Primeiro, vamos calcular a tensão média:

σ m é d = 0 + 0 2 = 0

Agora, vamos calcular o raio do círculo de Mohr:

R = 0 2 + 5 2 = 5 M P a

Logo, as tensões principais serão dadas por:

σ 1 = 0 + 5 = 5 M P a

σ 2 = 0 - 5 = - 5 M P a

Logo, teremos:

σ m á x = 7 M P a

σ i n t = - 5 M P a

σ m í n = - 5 M P a

Calculando-se a tensão cisalhante máxima:

τ m á x = ( σ m á x - σ m í n ) 2 = 7 - - 5 2 = 6 M P a

Resposta

σ m á x = 7 M P a

σ i n t = - 5 M P a

σ m í n = - 5 M P a

τ m á x = 6 M P a

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

As tensões principais que agem em um ponto em um corpo são mostradas na figura. Desenhe os três círculos de Mohr que descrevem esse estado de tensão e determine as tensões de cisalhamento máximas no p
Desenhe os três círculos de Mohr que descrevem cada um dos seguintes estados de tensão.
Desenhe os três círculos de Mohr que descrevem cada um dos seguintes estados de tensão.
O parafuso está preso a seu suporte em C. Se a força de 90 N for aplicada à chave para apertá-lo, determine as tensões principais e a tensão de cisalhamento máxima absoluta desenvolvidas na haste do p
O eixo maciço está sujeito a torque, momento fletor e força de cisalhamento como mostra a figura. Determine as tensões principais que agem nos pontos A e B e a tensão de cisalhamento máxima absoluta.