Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Concentradores de Tensões em Torção

Ver Todos os Exercícios

Teoria

Introdução

Vamos dizer que nós temos que calcular a tensão de cisalhamento máxima τ m á x no eixo abaixo:

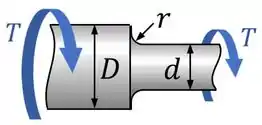
Nesse eixo, nós temos:

  • Uma seção inicial de diâmetro D ;
  • Uma seção final de diâmetro d ;
  • E uma redução de seção rápida entre essas seções, de acordo com o adoçamento de raio r .

Para calcular a tensão τ m á x nesse eixo, devemos, a princípio, aplicar a fórmula da torção τ = T c / J para a seção final, de diâmetro menor.

Mas na prática, por causa da redução rápida de seção sofrida por esse eixo, a tensão τ m á x vai ser ainda maior que T c / J para a seção de diâmetro menor.

Esse é o efeito que nós chamamos de concentração de tensões.

Então nesse caso...

Como podemos calcular τ m á x ?

Fórmula da Torção com Concentrador de Tensões

A resposta está em calcular τ m á x levando em conta o efeito da concentração de tensões através de um coeficiente K :

τ m á x = K T c J

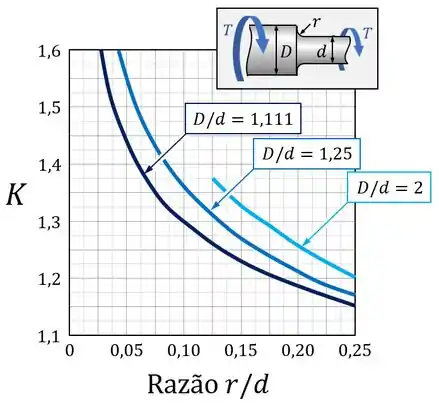
E, para saber o valor desse coeficiente de concentração de tensões K , nós devemos recorrer a um gráfico como o da imagem abaixo:

Uso do Gráfico

Para utilizar esse gráfico, devemos primeiro identificar o valor das dimensões do eixo no esquema na parte superior do gráfico.

Feito isso, devemos identificar qual curva do gráfico vamos usar. (Nesse caso, precisamos calcular a razão entre os diâmetros D / d para fazer a escolha dessa curva.)

E, por último, devemos calcular o valor da razão no eixo horizontal do gráfico. (Nesse caso, a razão entre o raio de adoçamento e o diâmetro menor r / d .)

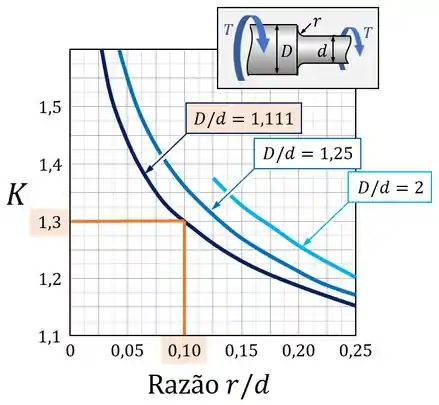
Feito isso, podemos inserir o valor dessa razão no gráfico e identificar o coeficiente K correspondente, como no exemplo abaixo:

Outros Casos

Além dos casos onde há uma redução rápida de seção, outros casos em que ocorre uma concentração de tensões em problemas de torção são:

  • Em acoplamentos entre dois eixos;
  • E em rasgos de chaveta em eixos para o acoplamento de engrenagens ou polias.

Apesar desses outros casos existirem, os exercícios focam sempre no caso principal, que é a redução rápida de seção.

Fórmula da Torção com Concentrador de Tensões

Uso do Gráfico

Outros Casos

Exercícios Resolvidos

Exercício Resolvido #1

Ferdinand P. Beer et al., Mecânica dos materiais, 5ª ed. Porto Alegre: AMGH, 2011, pp. 187 & 191-3.85.

O eixo de seção variável da figura gira a 450   r p m . Sabendo que r = 5,08   m m , determine a potência máxima que pode ser transmitida sem exceder a tensão de cisalhamento admissível de 51,7   M P a .

Utilize o gráfico abaixo para a determinação do coeficiente de concentração de tensão K :

Passo 1

O que está acontecendo?

O eixo gira a uma frequência f = 450   r p m , transmitindo uma potência desconhecida P , de forma a suportar um torque T :

T = P 2 π f

Ele possui um seção maior de diâmetro D = 150   m m e uma seção menor de diâmetro d = 125   m m , e, consequentemente, raio c = d / 2 = 62,5   m m .

Além disso, existe um adoçamento de raio r = 5,08   m m entre essas seções.

Nesse adoçamento, haverá uma concentrações de tensões na peça de tal forma que a tensão de cisalhamento máxima na peça τ m á x vai ser:

τ m á x = K T c J

Onde:

  • K é o coeficiente de concentração de tensão, que deve ser encontrado a partir do gráfico fornecido;
  • & c e J são o raio e o momento polar de inércia da seção de diâmetro menor, uma vez que ela vai ter a razão c / J maior, e, consequentemente, a tensão τ m á x maior;

E o que é que o exercício quer?

Ele quer a potência máxima P que pode ser transmitida pelo eixo de tal forma que a tensão cisalhante máxima na peça τ m á x não ultrapasse a admissível τ a d m = 51,7   M P a :

τ m á x ≤ τ a d m

Desenvolvendo a condição acima, é possível isolar P e encontrar seu valor máximo.

Passo 2

Então vamos pegar a nossa condição de projeto:

τ m á x ≤ τ a d m

E desenvolvê-la.

Primeiro, temos que, devido à concentração de tensões, τ m á x = K * T c / J .

Dessa forma, a nossa condição de projeto fica assim:

K T c J ≤ τ a d m

Em seguida, podemos aplicar a fórmula do torque T em função da potência P transmitida pelo eixo, deixando a condição assim:

K P 2 π f c J ≤ τ a d m

E depois, podemos aplicar a fórmula do momento polar de inércia J para uma seção transversal maciça e circular de raio c , deixando a condição assim:

K P 2 π f c π 2 c 4 ≤ τ a d m

Arrumando tudo, temos que:

K P π 2 f c 3 ≤ τ a d m

E, isolando a potência P , encontramos que:

P ≤ τ a d m π 2 f c 3 K

Agora, antes de podermos calcular essa expressão, temos que conhecer o coeficiente de concentração de tensão K .

Então vamos atrás dele.

Passo 3

Para encontrar o coeficiente K , precisamos recorrer ao seu gráfico:

Do gráfico, vemos que é necessário calcular as razões r / d e D / d .

Calculando essas razões, encontramos que:

r d = 5,08   m m 125   m m = 0,04

&

D d = 150   m m 125   m m = 1,2

Ao tentar inserir essas razões no gráfico, percebemos que não existe uma curva D / d = 1,2 .

Então vamos usar as curvas mais próximas ( D / d = 1,25 e D / d = 1,111 ) e usar para K um valor aproximado entre essas curvas.

Fazendo isso, encontramos que K ≅ 1,55 :

Passo 4

Agora, podemos voltar para a expressão que tínhamos:

P ≤ τ a d m π 2 f c 3 K

E substituir os valores:

  • τ a d m = 51,7   M P a = 51,7   N / m m 2 ;
  • f = 450   r p m = 450 * 1 / 60   s - 1 ;
  • c = 62,5   m m ;
  • & K = 1,55 ,

Para encontrarmos que:

P ≤ 51,7   N / m m 2 π 2 450 1 60 s - 1 62,5   m m 3 1,55

Calculando tudo isso, encontramos que:

P ≤ 602781487   N * m m * s - 1

Esse número é muito grande, então podemos reescrevê-lo em k N * m * s - 1 :

P ≤ 603   k N * m * s - 1

Agora pensa aí...

Newton ( N ) vezes metro ( m ) é o mesmo que Joule ( J ).

E Joule ( J ) por segundo ( s ) é o mesmo que Watt ( W ).

Então:

k N * m * s - 1 = k N * m s = k J s = k W

Sendo assim, temos que a potência máxima P que o eixo pode transmitir é:

Resposta

603   k W

Exercício Resolvido #2

Ferdinand P. Beer et al., Mecânica dos materiais, 5ª ed. Porto Alegre: AMGH, 2011, pp. 191-3.87.

Sabendo que o eixo de seção variável mostrado na figura deve transmitir 45   k W na velocidade de 2100   r p m , determine o raio r mínimo do adoçamento para que a tensão de cisalhamento admissível de 50   M P a não seja excedida.

Utilize o gráfico abaixo para a determinação do coeficiente de concentração de tensão K :

Passo 1

O que está acontecendo?

O eixo tem uma seção maior de diâmetro D = 60   m m e uma seção menor de diâmetro d = 30   m m , e, consequentemente, raio c = d / 2 = 15   m m .

Entre essas seções, existe um adoçamento de raio r .

Além disso, o eixo transmite uma potência P = 45   k W a uma frequência f = 2100   r p m , resistindo assim a um torque:

T = P 2 π f

E o que é que o exercício quer?

Ele quer saber o raio mínimo r de adoçamento para que a tensão de cisalhamento máxima no eixo τ m á x não ultrapasse a admissível τ a d m = 50   M P a :

τ m á x ≤ τ a d m

Sendo que, devido à concentração de tensões, sabemos que essa tensão máxima absoluta τ m á x , a b s vai ser:

τ m á x = K T c J

Onde:

  • K é o coeficiente de concentração de tensões, encontrado a partir de seu gráfico;
  • & c e J são o raio e o momento polar de inércia da seção de diâmetro menor, uma vez que ela vai ter uma razão c / J maior, e, consequentemente, uma tensão τ m á x maior.

E como vamos resolver o exercício?

Vamos primeiro calcular qual é o coeficiente K necessário para que a condição τ m á x ≤ τ a d m seja satisfeita.

Feito isso, vamos buscar no gráfico de K qual é o valor de r correspondente.

Passo 2

Então vamos pegar a nossa condição de projeto:

τ m á x ≤ τ a d m

E desenvolvê-la, com o objetivo de encontrar qual o coeficiente K necessário para satisfazê-la.

Primeiro, fazemos que τ m á x = K * T c / J , devido à concentração de tensões.

Fazendo isso, temos que:

K T c J ≤ τ a d m

Agora, podemos substituir a fórmula do momento polar de inércia J para uma seção circular maciça de raio c & a fórmula do torque T :

J = π 2 c 4

&

T = P 2 π f

Fazendo isso, temos que:

K P 2 π f c π 2 c 4 ≤ τ a d m

Arrumando tudo, isso fica assim:

K P π 2 f c 3 ≤ τ a d m

E isolando K , encontramos que:

K ≤ τ a d m π 2 f c 3 P

Agora, substituindo:

  • τ a d m = 50   M P a = 50   N / m m 2 ;
  • f = 2100   r p m = 2100 * 1 / 60   s - 1 ;
  • c = 15   m m ;
  • & P = 45   k W = 45000   N * m * s - 1 = 45 * 10 6   N * m m * s - 1 ,

Encontramos que:

K ≤ 50   N / m m 2 π 2 2100 1 60 s - 1 15   m m 3 45 * 10 6   N * m m * s - 1

Como dessa forma, todas as unidades vão se cortar, isso fica assim:

K ≤ 50 π 2 * 2100 1 60 * 15 45 * 10 6

Calculando tudo, isso dá aproximadamente:

K ≤ 1,3

Passo 3

Agora, vamos observar o nosso gráfico para K :

Primeiro, vemos que precisamos calcular a razão D / d para identificarmos qual curva do gráfico devemos usar.

Fazendo isso, temos:

D d = 60   m m 30   m m = 2

Destacando a curva D / d = 2 e traçando uma linha em K = 1,3 , vemos que uma estimativa para a menor razão r / d que satisfaz a condição K ≤ 1,3 é r / d = 0,175 :

Passo 4

Usando a estimativa do passo anterior, temos que:

r d ≅ 0,175

Isolando r , isso significa que:

r ≅ 0,175   d

Substituindo d = 30   m m , encontramos que:

r ≅ 0,175   ( 30   m m )

Calculando isso, encontramos nossa resposta final:

r ≅ 5,25   m m

Observação: Como esse resultado final é baseado em aproximações, é de se esperar que diferentes alunos obtenham resultados diferentes.

Valores como r ≅ 5   m m ou ≅ 5,5   m m também são boas aproximações!

Resposta

r ≅ 5,25

Por se tratar de uma aproximação, essa não é a única resposta possível, sendo respostas como r ≅ 5   m m ou r ≅ 5,5   m m também adequadas.

Exercício Resolvido #3

Elaboração própria

Um dos momentos mais tristes da história do automobilismo foi quando o famoso piloto de Fórmula 1, Ayrton Senna, faleceu em um grave acidente em uma corrida. Foi comprovado posteriormente que o manche do volante apresentava uma variação de seção e que essa foi a causa principal do acidente. O acidente ocorreu em uma curva em que o carro de Ayrton Senna estava em alta velocidade. Explique porque um manche variando de seção bruscamente é altamente perigoso para os pilotos de fórmula 1.

Passo 1

Uma variação brusca de seção em qualquer viga, peça mecânica ou peça estrutural causará o que chamamos de concentração de tensões. Essa concentração de tensão leva em consideração um coeficiente de concentração de tensão que potencializa as tensões que se concentram na região de mudança de seção. Quando analisamos os casos de carros de fórmula 1, sabemos que nas curvas os volantes são altamente solicitados por esforços de torção, se de fato o manche do volante apresentar variação de seção, significará que a tensão cisalhante média será aumentada pelo fator de concentração de tensões, esse aumento, dependendo da variação de seção, podendo causar a ruptura da peça, e potenciais acidentes. Analisando o enunciado podemos ver que a falha da peça ocorreu quando o carro estava em alta velocidade e para entrar em uma curva. Provavelmente o que ocorreu foi que o esforço torso causado pelo giro do volante gerou tensões cisalhantes médias. O problema está na variação de seção, pois nesse caso a tensão cisalhante média será multiplicada por um fator de concentração de tensão, que aumenta seu valor. O que ocorreu foi que a grande variação de seção aumentou a tensão cisalhante média ao ponto de chegar na tensão admissível do material, oque causou o rompimento da peça e o acidente fatal.

τ M a x = K   . τ m é d

τ M a x -> tensão cisalhante máxima

τ m é d -> tensão cisalhante média

K -> coeficiente de concentração de tensões (responsável por aumentar as tensões no ponto de concentração

Resposta

Ei, a resposta está no passo a passo :)

Exercício Resolvido #4

Elaboração própria

Em um experimento mecânico deseja-se descobrir o motivo do rompimento de uma determinada peça sujeita a ação de esforços de torção. A peça é mostrada abaixo e a região de rompimento é mostrado ao lado. Um aluno supõe que a provável causa do rompimento da peça foi um defeito de fabricação ou um defeito na soldagem do material. Com base em seus conhecimentos de resistência dos materiais indique qual foi o provável motivo do rompimento da peça e apresente conceitos plausíveis par sua suposição.

Passo 1

Sabemos que sempre que há uma variação brusca de seção em uma peça, ocorrerá uma concentração de tensão na peça. Essa concentração de tensões é contabilizada pelo coeficiente de concentração de tensões que é maior que 1, ou seja, ele aumenta o valor da tensão cisalhante nos dando valores mais altos do que em uma seção continua. Isso é comprovado pela fórmula.

τ M a x = K   . τ m é d

τ M a x -> tensão cisalhante máxima

τ m é d -> tensão cisalhante média

K -> coeficiente de concentração de tensões (responsável por aumentar as tensões no ponto de concentração

Podemos confirmar a contribuição do valor do concentrador de tensões analisando alguns gráficos que nos comprovam o seu aumento da tensão cisalhante.

Como nesse caso em que vemos que o menor valor possível de K é exatamente 1

Munido desse conhecimento podemos explicar o que ocorreu com a peça testada. A ação dos esforços de torção criou na peça tensões cisalhantes, como a peça possui uma variação brusca de seções isso causa uma concentração de tensões que é contabilizada pelo concentrador de tensões, que como já sabemos aumenta as tensões cisalhantes médias (que calculamos para uma seção continua). Oque provavelmente ocorreu foi que a mudança de seção foi tão brusca que a concentração de tensões aumentou a tensão cisalhante até o ponto de ultrapassar a tensão admissível, e nesse momento ocorreu a ruptura da peça.

Resposta

Ei, a resposta está no passo a passo :)

Exercício Resolvido #5

Elaboração própria

Dada a peça abaixo e sabendo que a seção varia bruscamente, determine qual será a tensão cisalhante máxima ao qual ela estará sujeita se o raio de adoçamento dessa peça for de 100mm.

Passo 1

Pra resolver esse exercício vamos dividir a solução em 3 partes. A primeira parte será definir o valor da tensão cisalhante média pela fórmula

τ = T . C J

Em que

T = t o r q u e  

C = r a i o   d a   m e n o r   s e ç ã o  

J = m o m e n t o   p o l a r   d e   i n é r c i a   d a   m e n o r   s e ç ã o    

Aqui vale lembrar que usamos os valores da menor seção pois é nela que ocorrerá a maior tensão cisalhante média, sempre lembre disso, usar os dados da menor seção, só usamos os valores da maior seção para definirmos o valor do coeficiente de concentração.

A segunda parte da nossa solução se trata de acharmos o coeficiente de concentração de tensão e para fazermos isso precisaremos de 3 coisas.

Primeiro usar um gráfico para determinar o coeficiente de concentração de tensão

Segundo devemos determinar qual a melhor curva do nosso gráfico para resolver o problema, e para isso usamos a relação

D d

Em que no nosso caso se trata da relação entre os diâmetros da nossa peça como mostra a figura

E por fim a terceira parte se trata de encontrarmos o valor no eixo horizontal do nosso gráfico, que encontraremos pela relação

r d

Por fim a terceira parte da nossa solução será relacionar a tensão cisalhante média com o coeficiente de concentração de tensão pela fórmula

τ m á x = K . τ

Passo 2

Agora que já sabemos como calcular cada termo vamos a prática.

Como vimos a primeira parte da solução se trata de calcularmos a tensão cisalhante média pela fórmula

τ = T . C J

Em que sabemos que

T = 322 K N . m  

C = 300 2 = 150 m m = 150   .   10 - 3 m

J = π . c 4 2 = π . 150   .   10 - 3 4 2 = 7,95.10 - 4 m 4

τ = 322   .   150   .   10 - 3 7,95.10 - 4 = 60755 K N m 2 = 60755 K p a = 60,755 M p a

Passo 3

Vamos agora determinar o coeficiente de concentração de tensão.

Sabemos que primeiro devemos usar um gráfico, que é esse aqui

Depois devemos determinar a melhor curva pela relação

D d = 5 00 300 = 1 , 6666

Agora que já sabemos a melhor curva só falta determinar o valor horizontal, que determinamos pela fórmula

r d = 100 300 = 0,33333

Agora vamos determinar o valor do K

K = 1,14

Passo 4

Agora basta relacionarmos a nossa tensão cisalhante média com o coeficiente de concentração de tensão pela fórmula

τ m á x = K . τ

τ m á x = 1,14   .   60,755 = 69,26   M p a

Resposta

τ m á x = 69,26   M p a

Exercício Resolvido #6

Elaboração própria

O manche de ligação de um volante foi construído segundo o formato abaixo. Se em uma curva a torção aplicada nesse eixe é a dada abaixo, e sabendo que o raio de adoçamento é de 10mm além da tensão cisalhante admissível ser de 1000 Mpa, determine se o eixo do volante romperia com a ação o esforço de torção.

Passo 1

Pra resolver esse exercício vamos dividir a solução em 3 partes. A primeira parte será definir o valor da tensão cisalhante média pela fórmula

τ = T . C J

Em que

T = t o r q u e  

C = r a i o   d a   m e n o r   s e ç ã o  

J = m o m e n t o   p o l a r   d e   i n é r c i a   d a   m e n o r   s e ç ã o    

Aqui vale lembrar que usamos os valores da menor seção pois é nela que ocorrerá a maior tensão cisalhante média, sempre lembre disso, usar os dados da menor seção, só usamos os valores da maior seção para definirmos o valor do coeficiente de concentração.

A segunda parte da nossa solução se trata de acharmos o coeficiente de concentração de tensão e para fazermos isso precisaremos de 3 coisas.

Primeiro usar um gráfico para determinar o coeficiente de concentração de tensão

Segundo devemos determinar qual a melhor curva do nosso gráfico para resolver o problema, e para isso usamos a relação

D d

Em que no nosso caso se trata da relação entre os diâmetros da nossa peça como mostra a figura

E por fim a terceira parte se trata de encontrarmos o valor no eixo horizontal do nosso gráfico, que encontraremos pela relação

r d

Por fim a terceira parte da nossa solução será relacionar a tensão cisalhante média com o coeficiente de concentração de tensão pela fórmula

τ m á x = K . τ

Passo 2

Agora que já sabemos como calcular cada termo vamos a prática.

Como vimos a primeira parte da solução se trata de calcularmos a tensão cisalhante média pela fórmula

τ = T . C J

Em que sabemos que

T = 200 K N . m  

C = 105 2 = 52,5 m m = 52,5   .   10 - 3 m

J = π . c 4 2 = π . 52,5   .   10 - 3 4 2 = 1,19   .   10 - 5 m 4

τ = 200 .   52,5   .   10 - 3 1,19   .   10 - 5 = 882353 K N m 2 = 882353 K p a = 882,35 M p a

Passo 3

Vamos agora determinar o coeficiente de concentração de tensão.

Sabemos que primeiro devemos usar um gráfico, que é esse aqui

Depois devemos determinar a melhor curva pela relação

D d = 115 105 = 1,1

Agora que já sabemos a melhor curva só falta determinar o valor horizontal, que determinamos pela fórmula

r d = 10 105 = 0,095 = 0,1

Agora vamos determinar o valor do K

K = 1 , 3

Passo 4

Agora basta relacionarmos a nossa tensão cisalhante média com o coeficiente de concentração de tensão pela fórmula

τ m á x = K . τ

τ m á x = 1 , 3   .   882,35 = 1147.1   M p a

Como a tensão admissível suportada pela peça do volante é de 1000Mpa vemos que o concentrador de tensões faria com que a tensão cisalhante máxima causasse o rompimento da peça.

Resposta

τ m á x = 1147.1   M p a

Como o cisalhante máximo é maior que o cisalhante admissível, o eixo romperia.

Exercício Resolvido #7

Elaboração própria

A peça de madeira abaixo possui as dimensões mostradas na figura. Sabendo que esse material possui tensão cisalhante máximo de τ a d m = 27   M P a e sabendo que essa peça possui concentração de tensão determine o máximo torque T que podemos aplicar nela sem que haja rompimento da mesma. O raio de adoçamento dessa peça é r = 5,8   c m .

Passo 1

Pra resolver esse exercício vamos dividir a solução em 3 partes. A primeira parte será relembrar como calcular tensão cisalhante média pela fórmula

τ = T . C J

Em que

T = t o r q u e  

C = r a i o   d a   m e n o r   s e ç ã o  

J = m o m e n t o   p o l a r   d e   i n é r c i a   d a   m e n o r   s e ç ã o    

Aqui vale lembrar que usamos os valores da menor seção pois é nela que ocorrerá a maior tensão cisalhante média, sempre lembre disso, usar os dados da menor seção, só usamos os valores da maior seção para definirmos o valor do coeficiente de concentração.

A segunda parte da nossa solução se trata de acharmos o coeficiente de concentração de tensão e para fazermos isso precisaremos de 3 coisas.

Primeiro usar um gráfico para determinar o coeficiente de concentração de tensão

Segundo devemos determinar qual a melhor curva do nosso gráfico para resolver o problema, e para isso usamos a relação

D d

Em que no nosso caso se trata da relação entre os diâmetros da nossa peça como mostra a figura

E por fim a terceira parte se trata de encontrarmos o valor no eixo horizontal do nosso gráfico, que encontraremos pela relação

r d

Por fim a terceira parte da nossa solução será relacionar a tensão cisalhante média com o coeficiente de concentração de tensão pela fórmula

τ m á x = K . τ

Como queremos determinar o valor do torque máximo nessa parte final teremos que

τ m á x = τ a d m

Passo 2

Agora que já sabemos como calcular cada termo vamos a prática.

Como vimos a primeira parte da solução se trata de calcularmos a tensão cisalhante média pela fórmula

τ = T . C J

Em que sabemos que

C = 29 2 = 14,5   C m = 14 , 5   .   10 - 2 m

J = π . c 4 2 = π . 14,5   .   10 - 2 4 2 = 6,94   .     10 - 4 m 4

Mas ainda não sabemos o valor de T

τ = T   .     14,5   .   10 - 2 6,94   .     10 - 4

Passo 3

Vamos agora determinar o coeficiente de concentração de tensão.

Sabemos que primeiro devemos usar um gráfico, que é esse aqui

Depois devemos determinar a melhor curva pela relação

D d = 47 29 = 1,6

Agora que já sabemos a melhor curva só falta determinar o valor horizontal, que determinamos pela fórmula

r d = 5,8 29 = 0,2

Agora vamos determinar o valor do K

K = 1 , 24

Passo 4

Agora basta relacionarmos a nossa tensão cisalhante média com o coeficiente de concentração de tensão pela fórmula

τ m á x = τ a d m = K . τ

τ a d m = 1,24   . T   .     14,5   .   10 - 2 6,94   .     10 - 4

Sabemos que

τ a d m = 27   M P a = 27000 K N m 2

Substituindo na nossa fórmula teremos que

27000 = 1,24   . T   .     14,5   .   10 - 2 6,94   .     10 - 4

Com isso descobrimos que

T = 104 ,   22   K N   .   m

Resposta

T = 104 ,   22   K N   .   m

Exercício Resolvido #8

Elaboração própria

A peça de aço abaixo possui as dimensões mostradas na figura. Sabendo que esse material possui tensão cisalhante máximo de τ a d m = 80   M P a e sabendo que essa peça possui concentração de tensão determine o máximo torque T que podemos aplicar nela sem que haja rompimento da mesma. O raio de adoçamento dessa peça é r = 2,27   c m .

Passo 1

Pra resolver esse exercício vamos dividir a solução em 3 partes. A primeira parte será relembrar como calcular tensão cisalhante média pela fórmula

τ = T . C J

Em que

T = t o r q u e  

C = r a i o   d a   m e n o r   s e ç ã o  

J = m o m e n t o   p o l a r   d e   i n é r c i a   d a   m e n o r   s e ç ã o    

Aqui vale lembrar que usamos os valores da menor seção pois é nela que ocorrerá a maior tensão cisalhante média, sempre lembre disso, usar os dados da menor seção, só usamos os valores da maior seção para definirmos o valor do coeficiente de concentração.

A segunda parte da nossa solução se trata de acharmos o coeficiente de concentração de tensão e para fazermos isso precisaremos de 3 coisas.

Primeiro usar um gráfico para determinar o coeficiente de concentração de tensão

Segundo devemos determinar qual a melhor curva do nosso gráfico para resolver o problema, e para isso usamos a relação

D d

Em que no nosso caso se trata da relação entre os diâmetros da nossa peça como mostra a figura

E por fim a terceira parte se trata de encontrarmos o valor no eixo horizontal do nosso gráfico, que encontraremos pela relação

r d

Por fim a terceira parte da nossa solução será relacionar a tensão cisalhante média com o coeficiente de concentração de tensão pela fórmula

τ m á x = K . τ

Como queremos determinar o valor do torque máximo nessa parte final teremos que

τ m á x = τ a d m

Passo 2

Agora que já sabemos como calcular cada termo vamos a prática.

Como vimos a primeira parte da solução se trata de calcularmos a tensão cisalhante média pela fórmula

τ = T . C J

Em que sabemos que

C = 17,45 2 = 8,725   C m = 8,725   .   10 - 2 m

J = π . c 4 2 = π . 8,725   .   10 - 2 4 2 = 9,10   .     10 - 5 m 4

Mas ainda não sabemos o valor de T

τ = T   .     8,725   .   10 - 2 9,10   .     10 - 5

Passo 3

Vamos agora determinar o coeficiente de concentração de tensão.

Sabemos que primeiro devemos usar um gráfico, que é esse aqui

Depois devemos determinar a melhor curva pela relação

D d = 34,90 17,45 = 2

Agora que já sabemos a melhor curva só falta determinar o valor horizontal, que determinamos pela fórmula

r d = 2,27 17,45 = 0,13

Agora vamos determinar o valor do K

K = 1 , 39

Passo 4

Agora basta relacionarmos a nossa tensão cisalhante média com o coeficiente de concentração de tensão pela fórmula

τ m á x = τ a d m = K . τ

τ a d m = 1 , 39   . T   .     8,725   .   10 - 2 9,10   .     10 - 5

Sabemos que

τ a d m = 80   M P a = 80 000 K N m 2

Substituindo na nossa fórmula teremos que

80 000 = 1 , 39   . T   .     8,725   .   10 - 2 9,10   .     10 - 5

Com isso descobrimos que

T = 60,03     K N   .   m

Resposta

T = 60,03     K N   .   m

Exercício Resolvido #9

Elaboração própria

A peça de latão abaixo possui as dimensões mostradas na figura. Sabendo que esse material possui tensão cisalhante máximo de τ a d m = 57   M P a e sabendo que essa peça possui concentração de tensão determine o máximo torque T que podemos aplicar nela sem que haja rompimento da mesma. O raio de adoçamento dessa peça é r = 1,1   c m .

Passo 1

Pra resolver esse exercício vamos dividir a solução em 3 partes. A primeira parte será relembrar como calcular tensão cisalhante média pela fórmula

τ = T . C J

Em que

T = t o r q u e  

C = r a i o   d a   m e n o r   s e ç ã o  

J = m o m e n t o   p o l a r   d e   i n é r c i a   d a   m e n o r   s e ç ã o    

Aqui vale lembrar que usamos os valores da menor seção pois é nela que ocorrerá a maior tensão cisalhante média, sempre lembre disso, usar os dados da menor seção, só usamos os valores da maior seção para definirmos o valor do coeficiente de concentração.

A segunda parte da nossa solução se trata de acharmos o coeficiente de concentração de tensão e para fazermos isso precisaremos de 3 coisas.

Primeiro usar um gráfico para determinar o coeficiente de concentração de tensão

Segundo devemos determinar qual a melhor curva do nosso gráfico para resolver o problema, e para isso usamos a relação

D d

Em que no nosso caso se trata da relação entre os diâmetros da nossa peça como mostra a figura

E por fim a terceira parte se trata de encontrarmos o valor no eixo horizontal do nosso gráfico, que encontraremos pela relação

r d

Por fim a terceira parte da nossa solução será relacionar a tensão cisalhante média com o coeficiente de concentração de tensão pela fórmula

τ m á x = K . τ

Como queremos determinar o valor do torque máximo nessa parte final teremos que

τ m á x = τ a d m

Passo 2

Agora que já sabemos como calcular cada termo vamos a prática.

Como vimos a primeira parte da solução se trata de calcularmos a tensão cisalhante média pela fórmula

τ = T . C J

Em que sabemos que

C = 36,5 2 = 18,25   C m = 18,25   .   10 - 2 m

J = π . c 4 2 = π . 18,25   .   10 - 2 4 2 = 1,74   .     10 - 3 m 4

Mas ainda não sabemos o valor de T

τ = T   .     18,25   .   10 - 2 1,74   .     10 - 3

Passo 3

Vamos agora determinar o coeficiente de concentração de tensão.

Sabemos que primeiro devemos usar um gráfico, que é esse aqui

Depois devemos determinar a melhor curva pela relação

D d = 40,15 36,5 = 1,1

Agora que já sabemos a melhor curva só falta determinar o valor horizontal, que determinamos pela fórmula

r d = 1,1 36,5 = 0,03

Agora vamos determinar o valor do K

K = 1 , 76

Passo 4

Agora basta relacionarmos a nossa tensão cisalhante média com o coeficiente de concentração de tensão pela fórmula

τ m á x = τ a d m = K . τ

τ a d m = 1 , 76   . T   .     18,25   .   10 - 2 1,74   .     10 - 3

Sabemos que

τ a d m = 57   M P a = 57 000 K N m 2

Substituindo na nossa fórmula teremos que

57 000 = 1 , 76   . T   .     18,25   .   10 - 2 1,74   .     10 - 3

Com isso descobrimos que

T = 308,8   K N   .   m

Resposta

T = 308,8   K N   .   m

Exercícios de Livros Relacionados

Determine a tensão de cisalhamento máxima em um eixo de seção transversal cheia de 38m m de diâmetro, quando ele transmite 75h p a uma velocidade de (a) 750r p m e (b) 1500r p m .
Três eixos e quatro engrenagens são utilizados para formar um trem de engrenagens que transmite 7,5 kW do motor em A para a máquina ferramenta em F. (Os mancais para o eixo são omitidos no esquema) Sa
Utilizando um valor de tensão de cisalhamento admissível igual a 50M P a , projete um eixo de seção transversal cheia, feito de aço para transmitir 15k W na velocidade de (a) 30H z e (b) 60H z .
O projeto de um elemento de máquina especifica um eixo com diâmetro externo de 40 mm para transmitir 45 kW. (a) Se a rotação for de 720 rpm, determine a tensão de cisalhamento máxima no eixo a. (b) Se
Um eixo de aço de 2,5 m de comprimento e 30 mm de diâmetro gira a uma frequência de 30 Hz. Determine a potência máxima que o eixo pode transmitir, sabendo que G=77,2 GPa, que a tensão de cisalhamento