Exercícios Resolvidos de Mínimos Quadrados e Reflexões

Enunciado

A3 T15 T16

Em com o produto interno usual, seja um subespaço não trivial. Sejam e respectivamente a projeção e a reflexão ortogonais com respeito a . Considere as seguintes afirmações:

é ortogonal a .

Qual das opções abaixo é CORRETA?

A afirmativa é falsa e é falsa.

A afirmativa é falsa e é verdadeira.

A afirmativa é verdadeira e é falsa.

A afirmativa é verdadeira e é verdadeira.

Passo 1

Afirmativa :

A vantagem dessas questões de projeção e reflexão sobre um espaço é que podemos generalizar elas como se estivessem no XD

Então temos algo assim:

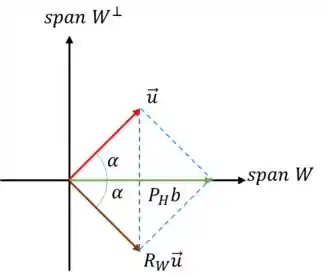
Como podemos ver, não é ortogonal a , mas sim pertence a ! Então essa é falsa.

Passo 2

Afirmativa :

O que essa relação aí te lembra? É Pitágoras! E quando Pitágoras vale? Para triângulos retângulos certo? Ou seja, isso aí só vale se e forem ortogonais, o que não necessariamente é verdade! Então essa é falsa.

Resposta

Letra

Exercícios de Livros Relacionados

1. Calcular o centróide dos vetores e representar geometricamente: u 1 = 1,2 e u 2 = 2,1 ; u 1 = 1,1 , u 2 = 1,2 , u 3 = 4 , - 1 e u 4 = 2,2 ; u 1 = 1,2 , 1 , u 2 = - 1 , - 2,0 e u 3 = 0,0 , - 1 ; u 1

3. Enunciar rigorosamente e provar: um operador linear do R n preserva os centróides.

4. Tomemos três vetores no R 2 , cujas extremidades formem um triângulo. Qual é o ponto do triângulo que coincide com a extremidade do centróide dos três vetores?

6. Calcular a projeção do vetor x , y , z ∈ R 3 sobre o sub-espaço gerado por 1,0 , 0 e 0,1 , 0 . Fazer uma figura.

5. Seja W o sub-espaço do R 4 gerado pelos vetores u 1 = 1,2 , 0,1 , u 2 = 2 , - 1,0 , 0 e u 3 = 0,0 , 1,0 . Calcular a projeção do vetor u sobre W nos seguintes casos: u = 3,1 , 2,2 ; u = 1,2 , 1,1 ;