Ciclones
Teoria
Introdução
Elutriadores e câmaras de poeira usam apenas o campo gravitacional para a separação, isto é, . Já ciclones, hidrociclones e centrífugas utilizam campos centrífugos e por isso conseguem campos bem maiores que . Como a velocidade terminal é diretamente proporcional ao campo, as partículas atingem maiores e menores partículas vão poder ser separadas.
Neste tópico, vamos ver os ciclones, que são equipamentos para misturas GÁS-SÓLIDO. Grava isso: gás-sólido! Outro ponto importante sobre eles é que têm razão de fluido ZERO.
Isto quer dizer que as partículas saem puras, sem nenhum fluido diluindo elas. Coloca-se um coletor de pó na base do ciclone para coletar as partículas. O resto (fluido e partículas não separadas) sai por cima.
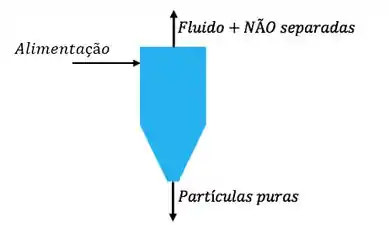
Pra que isso seja possível, a massa específica das partículas deve ser maior que a massa específica do gás!
Geometria
Ciclones são compostos por um corpo cilíndrico unido a um tronco de cone. Além disso, há um cilindro de diâmetro menor na parte superior, por dentro. Bora ver um desenho disso e dar nomes aos bois; a vista lateral é:
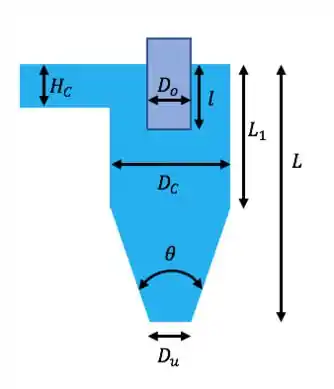
E a vista superior:
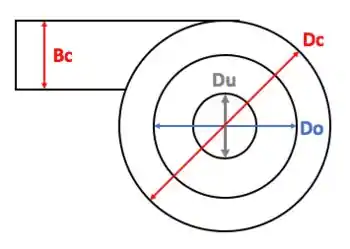
Repara que é a altura do duto de alimentação e é a largura dele. E importante: a entrada da corrente a ser separada é tangencial ao corpo cilíndrico. Por que isso é importante? Porque o fluido entra por ali e encontra aquele outro cilindro de diâmetro na frente dele. Isso faz com que o fluido gire em torno desse cilindro. E assim o gás vai fazer uma trajetória bem específica dentro do ciclone, tipo um vórtice (tem desenho mais pra baixo, fica tranquilo).
Outro ponto importante de saber é que é o principal parâmetro da geometria de um ciclone; as outras dimensões são relacionadas com . De acordo com as proporções entre as outras dimensões e o , os ciclones são agrupados em famílias. Por exemplo, um ciclone da família Lapple, sempre vai ter . Mas não se esquenta muito com gravar essas razões porque elas são tabeladas.
Eficiência de Separação
Antes de vermos fórmulas pra a eficiência em ciclones, precisamos entender um pouco como a separação é feita. As partículas alimentadas vão estar dispersas pela vazão alimentada; uma vez submetidas ao campo centrífugo (é sempre radial e aponta pra fora) dentro do ciclone, a velocidade terminal das partículas estará apontando para a parede do ciclone.
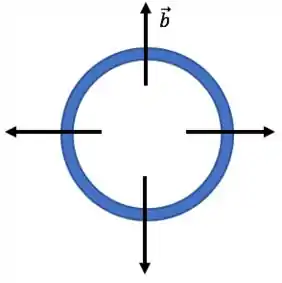
À medida que essas partículas vão descendo em um movimento em espiral por dentro do ciclone, acompanhando o movimento do fluido, elas também estarão andando em direção à parede do ciclone, por causa do campo centrífugo. Quando a partícula encosta na parede do ciclone, consideramos que ela está separada (porque ela vai cair e ser recuperada lá embaixo). Esse movimento em espiral é tipo assim:
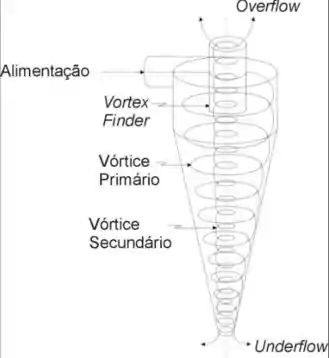
Fluido + partícula descem seguindo o vórtice primário. Quando o fluido chega lá embaixo (já com menos partículas, que foram sendo separadas), ele sobe num vórtice secundário até sair lá por cima (onde tá indicado o overflow). “Vortex Finder” é só o nome daquele cilindro lá de cima.
Embora partículas possam ser separadas nessa espiral ascendente (o vórtice secundário), a gente vai desconsiderar esse efeito, para ser mais conservador; pra gente, separação só durante a descida.
Agora, precisamos de dois conceitos: tempo de residência e tempo de queda.
- Tempo de residência é o tempo que a partícula permanece dentro do equipamento, no caso, o ciclone
- Tempo de queda é o tempo que a partícula leva para ser separada, que no caso, é o tempo que ela leva para tocar a parede do ciclone (tipo uma “queda lateral”)
O tempo de residência está relacionado à vazão de alimentação e é calculado por:
Em que é a velocidade do gás e é a área transversal do duto de alimentação. E não se preocupa com esse volume aí não; já já você vai entender onde eu quero chegar.
Já o tempo de queda, está relacionado com a velocidade terminal. Lembra que a definição da Física de velocidade é:
Aplicando ao nosso caso:
Daí:
Show! Agora que temos essas duas definições, bora lá! Pensa num ciclone aí: ele tem um certo volume e uma certa área transversal do duto de alimentação. Ok, agora não pode mudar esse ciclone hein! Haha Imagina que estamos alimentando uma dada vazão e lembra que:
Agora se resolvermos aumentar essa vazão para , como a área é constante, o que acontece é que a velocidade linear vai passar a ser , ou seja, dobra. Da mesma forma, a velocidade angular também vai dobrar. Vamos ver agora o que acontece com esses dois tempos que vimos:
Como , que está no denominador, dobra, o tempo de residência cai pela metade. Isso é ruim para a separação porque a partícula terá agora, menos tempo para ser separada. Mas antes de chegar a uma conclusão global do efeito, bora ver o que acontece com o tempo de queda:
E a velocidade terminal é diretamente proporcional ao campo centrífugo:
Eu já te falei que podemos calcular o campo centrífugo por:
Daí:
Como duplica ao dobrarmos a vazão , vai ser multiplicada por . E isso é muito bom para a separação já que:
Ou seja, o tempo de queda será reduzido por .
Daí, embora a partícula passe apenas metade do tempo no equipamento ao dobrarmos a vazão, ela é separada vezes mais rápido! Disso, concluímos que aumentar a vazão de alimentação aumenta a eficiência de separação.
Num gráfico, isso ficaria mais ou menos assim:
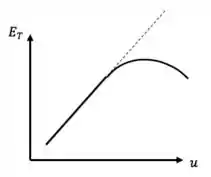
“Mas a gente não acabou de dizer que aumentar aumenta a eficiência de separação; então porque o gráfico não está subindo sempre?” Então.. esse efeito de crescer com tem um limite. Se a velocidade do fluido fica muito grande, acaba gerando turbulência dentro do ciclone e as partículas que já tinham sido recuperadas, acabam ressuspendendo. E aí a gente perde eficiência.
Mas enfim, bora continuar. Já que falamos de , deixa eu te contar uma coisa: geralmente, os ciclones trabalham com entre 6 e 20 m/s, pra ter uma separação legal e evitar ressuspensão. Se o problema não der o valor de , usamos a recomendação de projeto do Perry, que é:
E, finalmente, chegamos ao cálculo da eficiência. A fórmula para eficiência granulométrica, , para ciclones Lapple, é:
Para outras famílias de ciclone, existem outras fórmulas de . Mas geralmente usamos essa fórmula do Lapple mesmo que seja pra outra família; mas aí, dá uma olhada no formulário que você receber na prova; se só tiver essa fórmula para ciclones, é ela que você vai usar e, caso contrário, você usa a fórmula específica da geometria.
E, se nos interessar saber a eficiência total, , basta lembrar de:
E essa função de é assintótica em relação a , isto é, conforme aumenta, se aproxima de mas nunca ultrapassa; então, não precisamos nos preocupar em dividi-la em 2 intervalos, como fazíamos para câmara de poeira, por exemplo.
Ok, mas, até agora, não te falei nada sobre o de ciclones, né? E precisamos dele pra calcular eficiência. Daí vem a próxima parte e, diferentemente de novelas, não precisa esperar o próximo capítulo, é só continuar lendo : )
O número de Stokes
Primeiro de tudo, uma definição. Semelhante ao que fizemos nos outros equipamentos, aqui em ciclone também vai ter um diâmetro de corte , que vai ser o :
Isto é, é o diâmetro de partícula que sedimenta com de eficiência granulométrica.
Considerando que o sedimenta na região de Stokes e fazendo um desenvolvimento matemático, chegamos num número adimensional que se relaciona com :
“Tá... mas eu queria o para conseguir calcular e você me mostra que o é função do ...E aí? Continuo sem o ”.
Fica tranquilo aí, que a gente pode calcular a partir das dimensões do ciclone:
Em que é o número de espiras que são geradas no ciclone pelo movimento do fluido. Se não for dado, a gente assume 5 para Lapple!
Lembra que aquelas razões ali são fixas pra uma família de ciclones? Então o valor de também é fixo, de acordo com a família. Por isso, geralmente, a gente não precisa nem calcular ele, só pegar o valor que já tá tabelado mesmo!
Queda de pressão em ciclones
Outro ponto importante no projeto de um ciclone é conhecer a queda de pressão, , ao passar por um ciclone, porque isso vai ser importante pra projetar o ventilador/soprador que vai empurrar o fluido lá pra dentro.
Da mesma forma que podemos relacionar o número adimensional com , podemos relacionar o número de Euler (também adimensional) com o . E, assim como , o número de Euler é constante para uma família de ciclones e tabeladinho.
Ainda sobre queda de pressão, vai ser comum você ler tipo: “a queda de pressão é de metros de coluna de gás”. Confesso que a primeira vez que li algo do tipo eu estranhei, mas é mais fácil do que parece; é só lembrar de mecânica dos fluidos: o que a frase quis dizer é que o é igual à pressão causada por metros de gás, e isso calculamos por:
Em que, nesse caso, seria o .
Potência necessária ao soprador
Pra finalizar, pensa comigo: se tem uma queda de pressão no meio do caminho do meu fluido, vou ter que compensar essa perda dando energia, pressão pra ele né. Em se tratando de grandes volumes de gás, usamos um soprador e para calcular a potência dele usamos:
Em que:
Esse “TOTAL” é porque podem ter vários ciclones EM PARALELO e o soprador estar soprando uma carga que vai ser dividida para esses ciclones. Daí, tem que somar todas as vazões de cada um dos ciclones.
Eu destaquei o em paralelo porque se tiverem em série, a mesma vazão que passa por um depois passa pelo outro, então só conta uma vez mesmo.
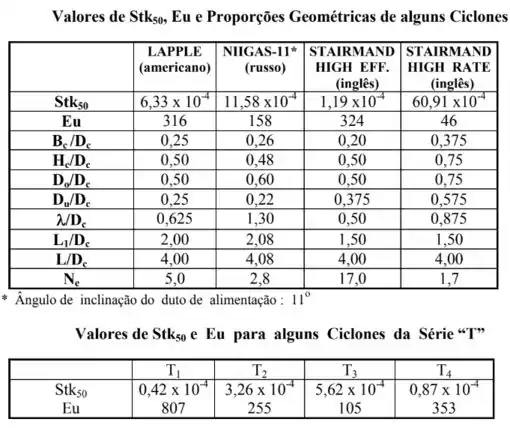
E ah, vou deixar aqui pra você uma tabela que vai ser bem útil para trabalhar com ciclones, porque tem os valores que são tabelados por família.
Eficiência de Separação
O número de Stokes S t k 50
Queda de pressão em ciclones
Potência necessária ao soprador
Exercícios Resolvidos
Exercício Resolvido #1
Massarani, G. ( 2002 ). Fluidodinâmica em Sistemas Particulados, 2 a e d .
A companhia Chalboud do Brasil adquiriu uma bateria de ciclones com as dimensões especificadas na figura abaixo para coletar partículas de um fluxo de ar a e . A densidade das partículas é .
Verificar a validade da seguinte especificação fornecida pelo fabricante: partículas com diâmetro maior que são coletadas com eficiência superior a quando a velocidade do ar na seção de alimentação do ciclone é .
Passo 1
Ao trabalhar com ciclones, a primeira coisa que temos que fazer é identificar a qual família o ciclone pertence (ou se é um Hidrogênio dos ciclones e não tem família haha).
Sabemos que as razões entre as diferentes dimensões e o são tabeladas. Já vou colocar logo a tabela aqui:
Bora calcular algumas dessas razões pro nosso ciclone pra descobrir a família dele:
Daí nosso ciclone se aproxima muito do Lapple.
Ok, agora vamos ver o que a questão pede. Basicamente, temos que verificar se para esse ciclone, em operação nas condições dadas, as partículas de estão associados com ; o que vamos fazer é ignorar essa afirmação completamente e calcular a eficiência. Depois a gente compara.
Passo 2
Recapitulando o que temos:
Para o ar a e 1 atm, encontramos os seguintes valores tabelados:
A massa específica do ar também poderia ser calculada considerando o ar como gás ideal. Nesse caso:
Como
Rearranjando:
Precisamos da temperatura em escala absoluta; passando pra Kelvin:
Daí
Indo atrás da do ar atmosférico:
Daí:
Repara que o tem um “litro” ali, que a gente vai precisar passar pra pra seguir trabalhando em CGS, ok?
O que mais o enunciado nos deu?
E as dimensões todas do ciclone. Show.
Passo 3
Para calcular a eficiência granulométrica de ciclones, usamos:
Mas ainda não temos . Então vamos usar o tabelado pra encontrar .
Já temos e. Só falta o . Bora calcular.
Sabemos tudo na direita. Daí, passando tudo pro CGS pra calcular:
Agora pega o tabelado e bora calcular o :
Passo 4
Agora que temos , é só usar a fórmula de pra calcular a eficiência granulométrica da partícula de .
Daí a afirmativa do enunciado é falsa porque.
Resposta
A afirmativa do enunciado é falsa porque.
Exercício Resolvido #2
UERJ – Prof. André Luís Alberton
Um ciclone Lapple deve processar uma suspensão gasosa diluída de ar atmosférico, visando a separação de partículas de com eficiência de A densidade do sólido é igual a 2100 . A pressão da alimentação é de e a temperatura é .
a) Dimensione o ciclone e determine a vazão que pode ser processada.
b) Qual a potência de um soprador requerida, sendo a eficiência do soprador igual a 60%?
Passo 1
A primeira coisa que temos que buscar no enunciado ao trabalhar com ciclones é qual a família; nesse caso, temos um ciclone Lapple. Daí, daquela tabela lá da teoria:
Como as relações entre as dimensões de um ciclone são tabeladas, basta determinar o e, sabendo de qual família se trata, nosso dimensionamento estará de boas.
E nós podemos obter o por:
Mas repara que ainda não temos algumas outras variáveis que entram aí. O que a gente sabe é que:
- Tenho as condições do gás, daí posso calcular e pesquisar sobre
- Através da informação da eficiência da partícula de , posso calcular o
- e posso escrever e em função de
Dessa forma, como o valor de é tabelado, só sobra uma variável a determinar e aí tiramos . Aí, voltamos e calculamos também.
Na letra b, vamos precisar usar o número de Euler para calcular a queda de pressão no ciclone e depois, pra calcular a potência, é só usar:
E, como só tem um ciclone, , em que é a vazão calculada no item a.
Pra esse exercício, vamos usar SI já que temos alguns dados nesse sistema. Mas você pode fazer como preferir!
Ah! Uma coisa: esse “suspensão gasosa DILUÍDA” nos diz que não precisamos fazer correção de concentração pra velocidade terminal.
Passo 2
Bora começar calculando o diâmetro de corte, . De “separação de partículas de com eficiência de ”, sabemos que, para , . Daí usando a expressão de para ciclones:
Eu vou resolver isso na HP Prime. Tem que ir na tecla que tem uma maletinha, depois “Solve”, depois “Zeros”. E você vai precisar lançar a forma homogênea da equação, que é quando está igualada a zero; é só passar o pro outro lado:
Mas esse comando “zeros” já entende que está igualado a zero; daí você só lança a parte da esquerda. Na sua tela, vai aparecer:
Aí, a HP me retornou:
Ou seja, ou . Como estamos falando de diâmetro, não faz sentido ser negativo. Daí:
Com podemos ir pro e calcular . Mas antes, precisamos das propriedades físicas do fluido.
Passo 3
Assumindo gás ideal, vale:
Como:
Rearranjando:
Precisamos da temperatura em escala absoluta; passando pra Kelvin:
Daí:
Pra do ar atmosférico, vamos considerar que ele é formado por 80% de gás nitrogênio () e 20% por gás oxigênio ().
Daí:
Indo atrás da viscosidade nessas condições:
Passo 4
Agora repara que:
Temos quase tudo, mas ainda falta a vazão . Lembra que:
Não temos nenhuma informação sobre ; nesses casos, como disse lá na teoria, usamos:
Quanto a e , podemos escrevê-los em função de , já que as relações entre eles são tabeladas. Olhando a tabela para Lapple:
Isolando e :
Jogando tudo isso na fórmula da vazão:
Agora, jogando tudo que temos na fórmula do , só vamos desconhecer o . O valor de é tabelada e, tendo uma equação e uma variável, achamos . Vou usar unidades do SI.
Calculando (repara que dá pra cortar um em cima e embaixo):
Usando a tabela, achamos todas as outras dimensões; por exemplo, como:
E ah! O enunciado pediu a vazão também, né? Como já achamos que:
Jogando o valor de :
Passo 5
Agora letra b: qual a potência de um soprador requerida, sendo a eficiência do soprador igual a 60%?
Falta só calcular a potência, mas antes disso, como:
Precisamos do . Falou de , lembra logo de Euler:
Só lembrando: esse no é a vazão que passa num ciclone apenas. Já o em é a vazão que passa pelo soprador, que vai ser o somatório das vazões que passam por ciclones em paralelo, caso existam. Nesse caso, só tem um ciclone então vão ser o mesmo valor.
é tabelado e a única coisa que não sabemos na expressão dele é o , daí:
Saiu em Pascal porque estou usando unidades do SI e essa é a unidade do SI pra pressão. A potência do soprador fica:
Resposta
- e
Exercício Resolvido #3
Elaboração própria
Um ciclone Stairmand HE de de diâmetro está tratando de ar a e 1 atm, contendo finos de ( e esfericidade 0,7). Devido a variações no processo industrial a granulometria do pó que chega ao ciclone aumentará em demasia. Desta forma, a fim de proteger o ciclone, será instalado um elutriador que deverá capturar todas as partículas maiores que , conforme o esquema abaixo.
Pede-se:
a) Calcular o diâmetro do elutriador.
b) Calcular a eficiência global do processo.
Dado:
e
Passo 1
Nessa questão, temos equipamentos em série. Na letra a, estamos interessados apenas no elutriador, já na b, é pedida a eficiência do conjunto daí vamos ter que “dividir” o problema em 3:
- Achar a expressão de para o elutriador
- Achar a expressão de para o ciclone
- Achar a expressão de para o conjunto, usando:
Com sendo o elutriador e o ciclone.
Depois, é só integrar em , isto é, na entrada do equipamento , e acharemos a eficiência global, :
AHH! Uma coisa importante: o enunciado NÃO deu a densidade do gás, mas deu as condições dele
e 1 atm
Assumindo gás ideal, vale:
Podemos escrever o número de moles como , com sendo massa de gás e sendo a massa molecular média. Rearranjando:
Trabalhando no CGS e usando em Kelvin:
Passo 2
- Calcular o diâmetro do elutriador.
Nos foi informado que o elutriador deverá capturar todas as partículas maiores que . Daí, vamos analisar o limite, que é a partícula de . Para ela:
Daí, achando , achamos . Como:
Com sendo a vazão volumétrica e a área transversal do elutriador.
Poderemos achar o diâmetro do elutriador, já que temos
.
Para achar , EU VOU ASSUMIR que a partícula sedimenta na região de Stokes; vou assumir porque no elutriador só tem a força gravitacional e a partícula é pequenininha, mas depois tem que conferir, ok?
Pra região de Stokes vale:
Com
Como é dado que
Daí, trabalhando com o CGS e usando , já que só há força gravitacional no elutriador:
Massssss, antes de continuar, tem que conferir se, com essa velocidade, realmente está na região de Stokes. Fazemos isso calculando o Reynolds. Se você calcular, vai ver que dá:
E, com esse Reynolds, realmente está na região de Stokes! OK!
Se você não quisesse ir por esse caminho, poderia ter aplicado as correlações de Coelho e Massarani de cara.
Passo 3
Agora que temos , podemos calcular o diâmetro do elutriador:
Como vou usar o CGS, preciso converter :
Daí:
E lembrando que:
Passo 4
b) Calcular a eficiência global do processo.
Como já disse lá no passo 1, vamos ter que usar:
Daí bora começar pelo que já está meio caminho andado: o elutriador. Assumindo elutriador ideal, vale:
Como vamos, depois, ter que integrar em , bora expressar esses limites em termos de logo:
Para :
Daí:
Passo 5
Indo, agora, para o ciclone. A fórmula de é:
Novamente, bora começar pelo mais fácil? Haha Vamos integrar em , daí vamos ter que colocar em função de . Fazemos isso usando a fórmula dada para . E repara que não precisa mexer em porque ele é um número.
Agora, bora achar o . Fazemos isso usando o , que é tabelado. Para Stairmand HE:
E a fórmula pra é:
Usando o CGS e substituindo tudo que temos:
Então podemos escrever do ciclone como:
Passo 6
Agora é só juntar tudo.
Como é definido em 2 intervalos, vamos ter que dividir em 2 intervalos também:
- Para :
- Para :
Daí nossa integral também vai ser divida em 2 intervalos:
Resposta
Exercício Resolvido #4
Elaboração própria
Uma unidade de separação foi dimensionada pra tratar eficientemente uma suspensão que chega a em volume. Essa unidade consiste em um ciclone e atinge exatamente a meta de separação.
Por mudanças no processo, a suspensão passará a chegar a em volume. O engenheiro responsável disse que a unidade não mais será capaz de realizar o tratamento e sugeriu adicionar um segundo equipamento para atingir a separação desejada. Sabendo que este equipamento é uma câmara de poeira:
Onde esta câmara deveria ser localizada preferencialmente? Antes ou depois do ciclone?
Passo 1
Esse enunciado não pede pra gente fazer conta nenhuma; é só explicar as coisas. Bora primeiro pegar algumas informações importantes do enunciado.
Ele diz que o ciclone da unidade que já existe atinge exatamente as metas quando a suspensão chega a , ou seja, se a suspensão chegar à uma concentração maior, a meta não será atingida.
Teve uma mudança no processo e agora a suspensão vai chegar a ; se só ficar o ciclone, a meta de separação NÃO será atingida e por isso o engenheiro propôs adicionar uma câmara de poeira, para complementar a separação.
Passo 2
Onde esta câmara deveria ser localizada preferencialmente? Antes ou depois do ciclone?
A gente sabe que o ciclone sozinho não vai fazer a separação; pra complementar adicionamos a câmara de poeira e agora temos duas possibilidades:
- Colocar a câmara antes do ciclone, de forma a diminuir a concentração na entrada do ciclone e atingir a meta
- Deixar a suspensão chegar à no ciclone, que vai ficar com uma saída com concentração acima da meta e depois colocar uma câmara de poeira pra diminuir mais essa concentração
As câmaras de poeira separam partículas apenas pela gravidade enquanto ciclones usam campo centrífugo de vários g, daí os ciclones conseguem pegar partículas menores do que a câmara de poeira.
Por isso, é jogo colocar a câmara ANTES do ciclone, dessa forma ela pega as maiores partículas e já diminui a concentração e depois o ciclone complementa a meta. Se colocássemos a câmara depois, talvez ela não conseguisse chegar na meta porque não conseguiria pegar as partículas menores.
Além disso, ao impedir que essas partículas maiores cheguem no ciclone, estaríamos o protegendo de erosão, que é uma das principais formas de “danificar” ciclones.
Resposta
Ei, a resposta está no passo a passo :)
Exercício Resolvido #5
Massarani, G. ( 2002 ). Fluidodinâmica em Sistemas Particulados, 2 a e d .
Deseja-se estudar o desempenho de uma bateria constituída por ciclones Lapple em série com respectivamente e de diâmetro no tratamento de de gás contendo em volume de sólido.
- Propriedades do gás: e
- Propriedades das partículas sólidas: e distribuição granulométrica dada por:
Pede-se:
- A eficiência global de coleta do sistema
- A potência do soprador para o serviço
Passo 1
Nessa questão, temos dois ciclones em série.
Tem uma vazão de gás “sujo”, a ser tratado, que passa pelo primeiro ciclone; um certo nível de separação ocorre e a vazão que sai desse primeiro ciclone vai, já mais “limpa”, para um segundo ciclone.
Sabemos que a vazão de alimentação é de . Como vou trabalhar no CGS, vou converter logo:
Essa vazão vai ser fixa nos dois ciclones, já que não há razão de fluido, isto é, as partículas saem puras, sem levar junto o fluido. Daí todo o fluido que sai de um ciclone vai para o outro. E, antes que você pergunte, eu sei que essa vazão não vai ser exatamente igual porque ela é a vazão de suspensão e a suspensão inclui partículas, que estão sendo parcialmente separadas. Mas repara que a concentração delas é baixa e não vai influenciar quase nada; é uma excelente aproximação dizer que é constante.
Agora, embora a vazão seja constante, o vai ser diferente em cada ciclone; esses ciclones são da mesma família e, para uma mesma família, é constante; acontece que o é diferente pra cada um deles e, por isso, a queda de pressão muda. Pra você visualizar melhor:
Pra finalizar essa introdução à questão, algo muitoooo importante: repara que ele dá a concentração volumétrica de partículas, que é . Embora essa concentração não seja tão importante no que diz respeito à vazão, vamos ter que considerar correção da velocidade terminal porque .
Passo 2
Para calcular a eficiência granulométrica global de equipamentos em série, temos que usar:
Em que é o do equipamento e é o do equipamento . Fisicamente, essa fórmula está nos dizendo que a separação granulométrica total é o que é separado no primeiro equipamento mais o que é separado do segundo , sendo que o que passa pela separação do segundo é só o que não foi separado no primeiro, daí o multiplicar por .
A expressão de ,para cada um dos ciclones, é:
E, como vimos na teoria, usamos o para obter o :
é tabelado e, de resto, na expressão, sabemos tudo menos . Daí equação e variável: solução única! Agora, vamos fazer assim: vamos, por um tempo, para o país das maravilhas com a Alice; enquanto a gente tiver lá, vamos fingir que não temos que corrigir a velocidade terminal e calcular para cada um dos dois ciclones; depois a gente volta pra realidade, ok? Vou chamar esses diâmetros de corte “imaginários” de . O é porque é relativo as condições de diluição infinita, sem efeito de concentração.
Para o primeiro ciclone:
Repara que eu passei a viscosidade de para , porque Poise que é a unidade do CGS pra viscosidade.
De forma semelhante, para o segundo ciclone:
Agora está na hora de voltar pra realidade. Um ciclone não separa as partículas por tamanho, quem faz isso é um filtro, por exemplo, mas, mesmo assim, nos referimos a DIÂMETRO de corte e não “alguma outra coisa” de corte; o ciclone separa partículas pela velocidade terminal delas, separa quando a partícula tem um tal que consegue bater na parede do ciclone antes de sair dele; sabemos relacionar diâmetro e e daí falar em diâmetros. Mas lembra disso: ciclone separa por velocidade.
Daí, para o primeiro ciclone, a só é chamada de diâmetro de corte porque tem uma tal que é separada com . Se tiver efeito de concentração, efeito extraterrestre, efeito de Júpiter ou qualquer outro (eu inventei estes dois últimos agora hein haha Não se assuta!), o ciclone não tá nem aí; ele continua na dele e a separação continua sendo por uma dada velocidade.
Acontece que, quando tem efeito de concentração, a velocidade terminal das partículas é alterada. Para o primeiro ciclone, por exemplo, precisamos achar qual é o diâmetro que nas condições de vai ter a mesma velocidade terminal da nas condições do país das maravilhas, ou seja, diluição infinita (concentração não afetando ), já que é a que amarra a separação.
Por esse último parágrafo, já sentiu um Coelho e Massarani no ar, né? Rs Bora lá! Temos um diâmetro, , e queremos a velocidade terminal dele nesse gás. Daí, vamos por:
Agora, pra achar o :
Precisamos de e ; como o enunciado não falou nada sobre esfericidade, vou assumir .
Calculando:
E, como isso tudo veio da condição de diluição infinita, esse é o :
Ok. Achando a dessa partícula:
Trabalhando com tudo no CGS:
Daí essa velocidade de é a “velocidade de corte”, a velocidade associada com . A questão agora é descobrir qual é o tamanho de partícula que, nas condições de , vai ter essa velocidade, ou seja, descobrir o tamanho de partícula associado a .
Passo 3
Para descobrir o tamanho de partícula associado a , vamos ter que fazer a correção “inversa” de concentração e descobrir a dessa partícula. Depois, relacionamos essa com diâmetro. Vem comigo que vai ficar tudo mais claro. A fórmula pra correção de concentração é:
Em que o valor de do é calculado de forma diferente dependendo do :
Com sendo o Reynolds calculado supondo que a esfera está isolada.
Calculamos o para a partícula e NÃO para essa real do equipamento com . Mas repara que achamos pra primeira , que é bem menor que . Vou assumir que esse novo vai, também, ser menor que e usar . Sim, esse é um caminho iterativo mas não tem muito por onde fugir; se chegar lá na frente e o for maior que , temos que voltar pra esse ponto...mas com uma folga dessas que temos, provavelmente não vai ser não.
Ok, aplicando:
Agora, temos uma velocidade e queremos saber o diâmetro correspondente:
Calculando
Oba! Reynolds menor que ! Não precisa voltar pra iterar. Bora continuar. Quem é o diâmetro que tem essa velocidade?
E, depois disso tudo, achamos o para o primeiro ciclone!
Fizemos isso tudo pro primeiro ciclone devido a nele. Para o segundo, será que precisa? Parte das partículas são separadas no primeiro então, talvez, seja menor que o segundo e não precisaremos corrigir. Então, guarda essa informação de para o primeiro ciclone e bora calcular a eficiência dele.
Passo 4
A fórmula de para ciclone é:
Para o primeiro ciclone, fica:
Para saber quanto de partículas foi separado no primeiro ciclone, não basta a eficiência por tamanho... precisamos da eficiência global, , que obtemos integrando de até , para varrer todos os diâmetros.
Como vamos integrar em , precisamos escrever em função de . Daí bora dar uma olhada na curva que o enunciado deu:
Manipulando:
Jogando em :
É nessa hora que a gente fica muito grato a quem inventou as calculadoras haha Calculando isso aí:
Agora, concorda comigo que as partículas que vão pro segundo ciclone são as que NÃO são separadas do primeiro, isto é, (? Então, chamando de a concentração volumétrica na entrada do ciclone e de a concentração volumétrica na entrada do segundo:
UFA! Como , não precisamos corrigir nada no segundo.
Passo 5
Escrevendo a expressão de para o conjunto:
Como o problema pede a eficiência global, temos que integrar:
Jogando esse monstro na calculadora:
Passo 6
b) A potência do soprador para o serviço
O pior já foi. Agora só falta a potência.
Como os ciclones estão em série: , porque a vazão que passa por um é a mesma que passa pelo outro...são as mesmas moléculas do fluido; passam por um e depois vão pro outro.
Temos que nos preocupar só com o , porque a queda de pressão total no sistema é a soma das quedas no primeiro e segundo.
Então, bora calculá-las! Temos que usar Euler, que é tabelado.
Para o primeiro ciclone:
Para o segundo:
Daí:
Como o enunciado não deu a eficiência do soprador, vamos ter que supor uma. Não me bate! É isso mesmo haha Vou supor . Daí:
Só pra ficar mais bonitinho, vou passar essa potência pra HP (horse power, ok? Não a calculadora haha)