Teoria
Introdução
E a próxima forma de separação que vamos ver é a filtração. Ao longo desse e dos próximos tópicos você vai perceber que a torta vai acabar sendo mais importante para a separação do que o próprio filtro. O filtro nada mais é do que um meio poroso usado para reter sólidos e deixar líquido passar. Mas o que é essa tal de torta?

Oops! Imagem errada. Infelizmente, não tem nada a ver com doce haha. Temos uma suspensão com partículas e fluido pra separar, né? Conforme essa suspensão vai passando pelo filtro, as partículas ficam retidas e vão se acumulando, formando um aglomerado, que chamamos de torta ou bolo.
Ah! Antes que eu esqueça: filtração é um problema TRANSIENTE já que as coisas mudam em função do tempo.
Tipos de filtração
Antes de falar dos tipos de filtração, quero te falar uma palavra que você provavelmente nunca deve ter ouvido: COLMATAR. Ela tem o mesmo sentido de “entupir”. Agora que você tá mestre em português, bora voltar pra Operações; existem dois tipos de filtração:
- Filtração em profundidade: nesse tipo, o filtro vai tendo seus poros colmatados ao longo da operação; daí tem-se um escoamento em meio poroso com permeabilidade e fator (de Forchheimer) alterando ao longo da operação.
- Filtração em superfície: nesse modo, eu NÃO quero que os poros sejam colmatados daí projeto meio filtrante para NÃO reter as menores partículas. O lance é que as maiores vão sendo retidas e formam a torta e ela sim retém tudo. Nessa forma, é comum recircular o filtrado no começo, que passou com partículas.
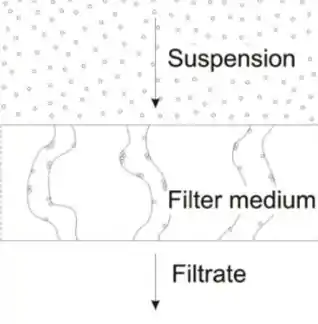
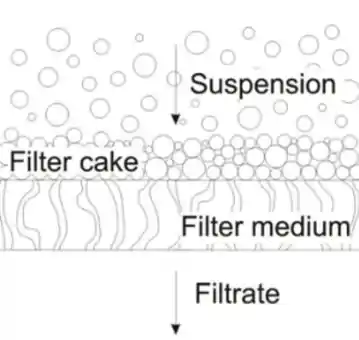
Auxiliar de filtração
Mas será que tudo sempre funciona perfeitamente do jeito que eu quero? Infelizmente, não.

Pode acontecer da sua torta colmatar, isto é, as partículas vão ficando tão grudadas umas nas outras e tão próximas que entopem o filtro. Nesses casos, vamos usar auxiliares de filtração, que são alguma coisa que você adiciona na suspensão pra evitar colmatação.

Mas pode ocorrer também de não ser a torta que está colmatando contra sua vontade e sim o filtro. Aí, podemos antes de passar a suspensão, passar um liquido só com auxiliar de filtração para formar uma pré capa.
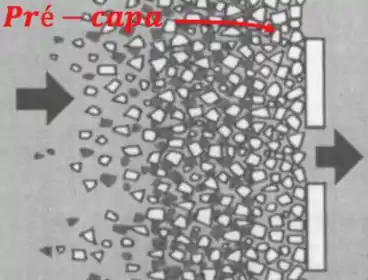
Filtração com formação de torta compressível
Pro equacionamento, vamos considerar algumas hipóteses:
- Escoamento Darcyano, unidirecional e de fluido newtoniano incompressível.
- A velocidade independe da posição na torta
- São desprezíveis os termos de aceleração, e campo (daí tá considerando filtração a graus do campo)
- e dependem da pressão nos sólidos
Daí já tem uma definição:
Em que:
Partindo da equação do movimento e fazendo todas as simplificações, chegamos em:
E, como assumimos escoamento Darcyano:
Vamos precisar adotar um eixo pra conseguir trabalhar com esses vetores melhor; vou aproveitar e já te mostrar também o perfil da pressão em função do espaço:
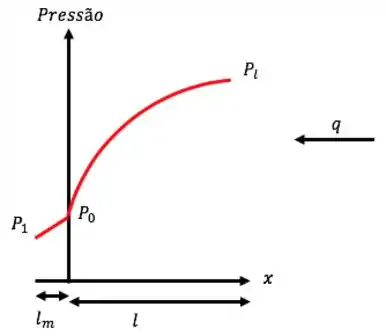
Repara que chamei:
Voltando lá pra nossa equação:
Agora, repara que é a pressão que chega na cabeça da torta; ela só depende do que vem antes (a bomba, por exemplo) e NÃO da torta. Considerando-a constante e lembrando que a derivada de constante é zero, podemos escrever:
Também vamos querer escrever a massa partículas do volume e, como a área transversal é constante, em função de :
Juntando tudo:
Definindo como a resistividade local da torta:
Integrando na torta:
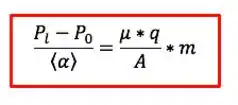
Em que é a resistividade média da torta.
Podemos, também, isolar a queda de pressão ; chamando de :
Acontece que vai ter um recipiente pras partículas ficarem retidas na filtração e vai ser mais fácil medir volume do que massa. Pra nos facilitar, tem a concentração :

Matematicamente:
O primeiro termo do denominador é referente a massa de líquido no filtrado (é o que PASSOU pela torta) e o segundo é referente à quantidade de líquido que ficou retida na torta. E:
Daí, desprezando o segundo:
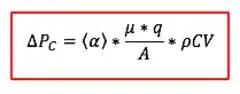
Queda de pressão no filtro
Vamos precisar saber, também, a queda de pressão no filtro em si. Partindo da equação do movimento e a simplificando:
Em que é o do meio filtrante.
Integrando:
Definindo como a resistência do meio filtrante:
Aí, resolvendo a integral e chamando de :
Queda de pressão no filtro como um todo
Podemos escrever:
Substituindo as expressões que já achamos pra cada um dos dois:
Colocando alguns termos em evidência:
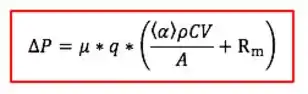
Podemos também fazer aparecer tempo e volume aí. Lembra que:
Substituindo, temos a equação para trabalhar com filtração que mais vamos usar:
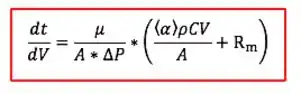
Determinação experimental de parâmetros
Para o caso de constante, separando o e da equação anterior e integrando:
Integrando e arrumando:
E isso é uma reta! Tendo pontos relacionando e podemos plotar um gráfico e fazer regressão linear.
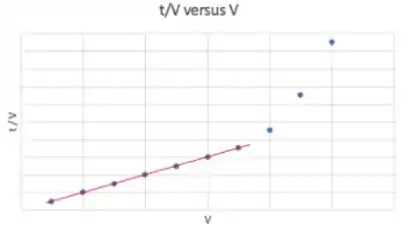
Repara que pra volumes mais altos (ou seja, numa fase mais avançada da operação, depois de um certo tempo) foge da linearidade. A explicação pra isso é QUADRO CHEIO. Tem um espaço pras partículas ocuparem no filtro, quando enche, o tempo aumenta, mas fica praticamente inalterado.
IMPORTANTE: Quando usamos bombas centrífugas, a carga fornecida pela bomba depende da vazão:
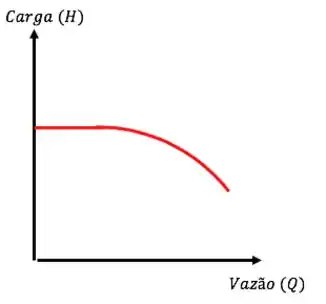
No começo da operação as vazões são maiores daí o NÃO vai ser constante e o gráfico também vai fugir da linearidade no começo. No meio da operação, antes do quadro encher, as vazões vão ser menores e o aproximadamente linear.
Nós fazemos regressão linear só na parte linear! Cuidado com isso, ok?
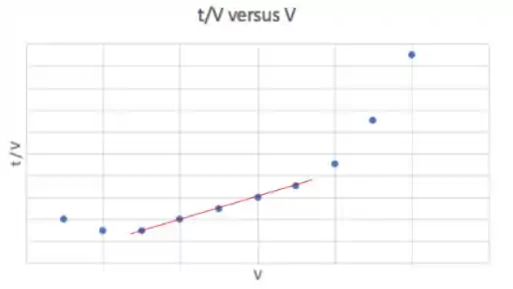
Resistividade da torta
Só uma coisa pra finalizar.
E quanto mais compressível maior é o .
Queda de pressão no filtro
Queda de pressão no filtro como um todo ∆ P
Determinação experimental de parâmetros
Resistividade da torta
Exercícios Resolvidos
Exercício Resolvido #1
Elaboração própria
Calcule a concentração de uma suspensão que foi filtrada. Foram obtidos de filtrado e um volume de torta com porosidade .
Dados:
- Partículas são )
- Fluido é água
Passo 1
Primeiro de tudo, bora lembrar da definição da concentração :

Matematicamente, isso fica:
Precisamos agora calcular cada um desses termos.
Passo 2
Primeiro, bora calcular o volume de líquido retido na torta. Lembrando que porosidade é:
Daí:
Lembrando da definição de densidade:
Daí a massa de líquido retido na torta é:
Por diferença no volume de torta, achamos o volume de partículas:
Usando a definição de densidade:
Agora só falta calcular a massa de líquido no filtrado, que é o termo :
Calculando :
Repara que eu podia ter jogado tudo na fórmula, mas fiz passo a passo caso você esqueça a fórmula ou só tenha a definição escrita mesmo no formulário : )
Resposta
Exercício Resolvido #2
Elaboração própria
Calcule a concentração de uma suspensão a ser filtrada que possui concentração .
Dados:
- Partículas são )
- Fluido é água
Passo 1
Essa questão é um pouco diferente da anterior. Aqui ainda nem filtramos a suspensão, então não tem como usar informações da torta. Mas calma que é só usar a definição:

Temos a concentração volumétrica da suspensão então conseguimos separar o volume de partículas do volume de fluido e usando as densidades de cada um deles calculamos as massas.
Passo 2
Temos . Bora adotar uma base de cálculo de . Daí:
Lembrando da definição de densidade:
Daí, para partículas:
Já pra o fluido:
Calculando :
Resposta
Exercício Resolvido #3
UFRJ. Medronho, Lista 5
Um filtro-prensa (um quadro de ) foi utilizado na filtração, em laboratório, de uma suspensão aquosa de barita ( de sólido/L de suspensão). De acordo com a curva obtida ao se lançar versus , pede-se:
a) Estimar o parâmetro (razão entre volume de filtrado e volume de torta) para o quadro cheio.
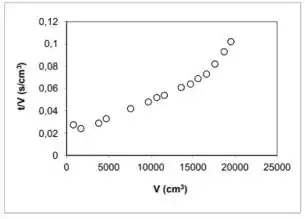
Passo 1
Nessa questão temos que calcular a relação entre o volume de filtrado e o volume de torta, que é o .
Daí, vamos ter que usar um ponto da operação em que saibamos tanto o volume de filtrado como o volume de torta obtidos até aquele momento.
Passo 2
a) Estimar o parâmetro (razão entre volume de filtrado e volume de torta) para o quadro cheio.
Essa é bem de boas; a definição de é:
Bora obter cada um dos termos que aparece:
Quando o quadro está cheio, sabemos que o gráfico de sai da linearidade. Daí, podemos pegar o último ponto dentro da linearidade e estimar o valor de nesse ponto como o volume de filtrado quando o quadro enche. Usando o gráfico dado:
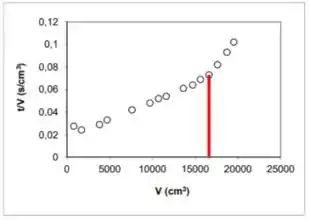
E, quando o quadro está cheio, o volume de torta é o próprio volume do quadro, certo? E as dimensões do quadro nós temos e são:
E sabemos também que há apenas UM quadro, daí o volume de torta, , com quadro cheio, é:
Convertendo as dimensões pra centímetros, para ficar com as mesmas unidades de :
Aí pra achar é só fazer a divisão:
Só quero fazer um comentário: nem toda área da face do quadro é disponível pra torta ocupar... somente a área efetiva! Mas NÃO temos nenhuma informação sobre a porcentagem efetiva e por isso considerei , mas saiba que é menor, ok?

SEEEE o enunciado tivesse dito a marca do quadro, poderíamos ir atrás de informações do fabricante para achar a área efetiva da face, mas não foi o caso.
Resposta
Exercício Resolvido #4
UFRJ. Medronho, Lista 5
Um grupo de alunos do curso de Engenharia Química da UFRJ obteve os seguintes resultados ao realizar a prática de filtração no filtro prensa do laboratório da Escola de Química:
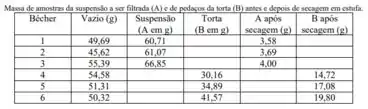
São dados:
− O experimento foi conduzido com uma suspensão aquosa de ().
− Queda de pressão no filtro: ;
− Área da face do quadro igual a e espessura do quadro igual a
− Número de quadros igual a .
− Tempo de filtração versus volume de filtrado :
![]()
Pede-se:
a) Determinar os parâmetros e .
b) Calcular a área total de filtração industrial para uma espessura de torta de e um volume final de filtrado de .
Passo 1
Vimos, na teoria, que para filtração vale:
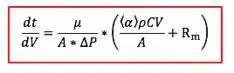
Para o caso de constante, separando o e da equação anterior e integrando:
Integrando e arrumando:
Agora temos que pegar os pontos relacionando e , plotar um gráfico e fazer regressão linear; daí tiramos os parâmetros e . Os outros termos que aparecem na equação nós temos, com exceção de e , que ainda teremos que calcular. Bora organizar nossas informações, usando tudo no sistema CGS.
Não temos porque esta é a área TOTAL de filtração, e o que nos foi dado é a área de UMA face. Para achar a área TOTAL de filtração precisamos lembrar que, em cada quadro, a área de filtração é duas vezes a área da face, pois há filtração dos dois lados no quadro. E, também, temos que multiplicar pelo número de quadros, que no caso é . Daí:
É dito que a suspensão é aquosa, mas não se fala a temperatura. Vou considerar que esteja a daí:
Passo 2
Para o cálculo da concentração , vamos usar os dados dos experimentos. A definição dessa concentração é:

Bora dar uma olhada nos experimentos relativos à concentração:

Tem 3 experimentos. Daí vamos calcular para cada um deles e depois usar a média. Organizando os cálculos numa tabela e lembrando que:

Usando a média desses três:
Passo 3
- Determinar os parâmetros e .
Como já vimos lá no passo 1, temos que plotar e fazer regressão linear. Usando as unidades do CGS, isto é, tempo sem segundos e volume em , os dados plotados ficam:
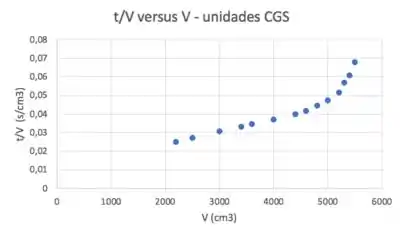
A regressão linear fazemos só com a parte linear do gráfico, lembra? Os outros pontos nós descartamos. Vou pegar até o ponto com porque está bemmm linear haha
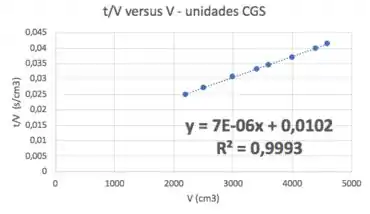
Agora é só comparar a equação obtida com a regressão com a desenvolvida teoricamente:
Isto é:
Daí:
E
Usando tudo no CGS, temos:
E
Isolando-os e fazendo as continhas:
Passo 4
b) Calcular a área total de filtração industrial para uma espessura de torta de e um volume final de filtrado de .
Agora temos que projetar um filtro industrial baseado nesses experimentos aí. Podemos escrever a área total de filtração industrial e função das medidas na escala piloto como:
E temos que:
Pelo gráfico do experimento, vemos que o gráfico foge da linearidade em , daí:
E o enunciado pede que:
Daí:
Resposta
- e
Exercício Resolvido #5
UFRJ. Medronho, Lista 5 - Adaptado
Um filtro-prensa (um quadro de xx) foi utilizado na filtração, em laboratório, de uma suspensão aquosa de barita ( de sólido/L de suspensão). De acordo com a curva obtida ao se lançar versus , pede-se:
Calcular os parâmetros e ; caso dependam de parâmetros desconhecidos, deixar indicado o cálculo.
OBS:
- A lavagem não é necessária;
- O tempo de desmantelamento, limpeza e montagem é estimado em .
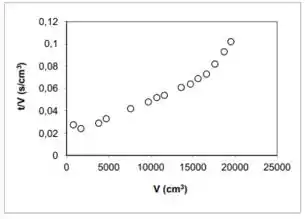
Considere a área de filtração igual a:
Passo 1
Lá na teoria, vimos que, partindo da equação do movimento, chegamos na equação de trabalho para filtração:
E, integrando-a ao longo do filtro, à constante, chegamos em:
Essa equação aí representa uma reta e podemos usá-la pra determinar parâmetros com base em experimentos, que é exatamente o que essa questão pede :) Mas temos que lembrar de só pegar os pontos que estão alinhados no gráfico!
As informações de lavagem e tempo de desmantelamento, limpeza e montagem não vamos usar pra nada, mas repara que aparece a concentração na fórmula da reta que achamos:
E essa concentração temos como calcular já que:

Passo 2
A primeira coisa que vou fazer é calcular logo a concentração :

Nos foi informado que a suspensão de trabalho é aquosa e de barita, com concentração de sólido/L de suspensão. Daí:
Nesse 1 litro de suspensão, sabemos a massa de sólido, . Usando a densidade da barita, determinamos esse volume de sólido :
Daí:
A densidade da barita não foi dada, mas é tabelada então temos como achar:
Só lembrar que, como a massa está em gramas, vamos usar a densidade em , para ficar com unidades compatíveis. Daí o volume vai sair em .
Ok, tendo o volume de sólidos, podemos calcular o volume de água:
Como volume de sólidos está em , vou passar o litro pra também, pra deixar tudo com mesmas unidades, né.
Ok, mas para calcular precisamos da MASSA de líquido, e não do volume... Novamente, usamos densidade, mas agora a da água:
A densidade da água varia com a temperatura e, como não temos a temperatura, poderíamos fazer duas coisas:
- Assumir que a densidade da água é por volta de então usar esse valor
- Deixar a densidade indicada
Como o enunciado disse para deixar indicado o que fosse desconhecido, vou pelo segundo caminho.
De qualquer maneira, como “temos” a massa de sólidos e a de água, podemos calcular :

Passo 3
Agora que já calculamos a concentração , podemos partir pra análise do gráfico:
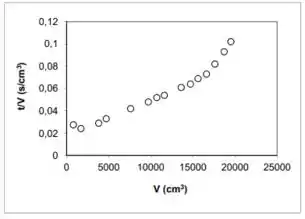
Vimos que a parte LINEAR pode ser descrita por:
Comparando essa equação com à de uma reta:
Temos que o coeficiente angular é:
E o coeficiente linear é:
Agora, traçamos a melhor reta possível para os dados na parte linear; como já temos o gráfico, não vale a pena pegar ponto a ponto e fazer regressão linear; mais vale traçar a reta na mão mesmo, ou no computador no caso hahah
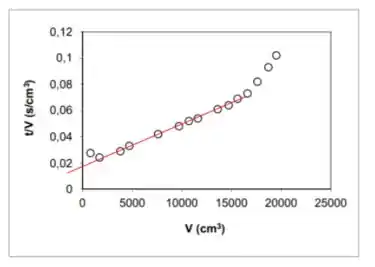
E foi assim que EU tracei... Se você tiver traçado um pouco mais pra cá, ou um pouco mais pra lá, tá de boas; só tem que lembrar de desprezar o primeiro ponto e os últimos 3, porque fogem da linearidade.
Agora, vendo pelo gráfico, podemos pegar os coeficientes linear e angular. Começando pelo linear, que é o valor de quando a reta cruza o eixo , isto é, quando :
Já o angular, pegamos pela tangente da reta com o eixo x. Temos que usar pontos em cima da reta que traçamos!!! E NÃO necessariamente pontos experimentais, ok? Vou usar, para o cálculo, os pontos:
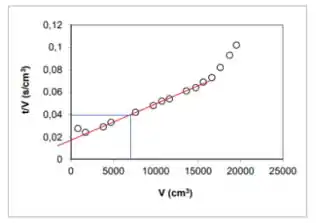
Passo 4
Acabamos de calcular os coeficientes linear e angular da reta experimental:
Agora, comparamos os valores calculados com a expressão pra cada um deles:
Daí:
Nos é pedido pra calcular os parâmetros e , daí bora isolá-los nessas expressões:
E agora é só substituir tudo que temos, que no caso são só:
Daí:
E é só até aqui que conseguimos chegar com os dados fornecidos.