Teoria
Introdução
Imagine que a gente vai projetar um equipamento de separação pra tirar partículas de um gás e que nesse equipamento vamos ter uma das saídas só com partículas, puras. Eu não quero perder minhas partículas então quero colocar um coletor nessa saída de partículas. Ok, mas onde é essa saída? No fundo do equipamento? Na frente? Em cima? Pela lateral? Precisamos descobrir...
Para responder essa pergunta, precisamos saber como as partículas se comportam no fluido em escoamento, como é o movimento delas. É isso que nós vamos ver nesse tópico : )
Movimento de partícula suspensa em um fluido escoando entre placas planas paralelas
Antes de tudo, deixa eu te dizer as duas hipóteses pro nosso desenvolvimento:
- Escoamento unidimensional do fluido
- Vamos desprezar a fase transiente do movimento da partícula
Vamos, primeiro, visualizar esse movimento. Pensa num rio, que é um fluido né; se uma pedrinha cai nele, ela vai sendo arrastada na direção do movimento da água, certo? Da mesma forma, uma partícula suspensa num fluido vai ter algum movimento, velocidade na direção do fluido.
Agora, pensa nessa mesma pedra que está sendo arrastada. Ela vai ficar na superfície da água eternamente??? Não né! Ao mesmo tempo que ela vai sendo arrastada, ela vai afundando. Daí, além de uma velocidade na direção da velocidade do fluido, ela vai ter uma velocidade para baixo, em direção ao fundo do rio, que está associada ao peso dela. Lembrando que peso é massa vezes gravidade, essa velocidade para baixo (velocidade de sedimentação) está associada com o campo gravitacional.
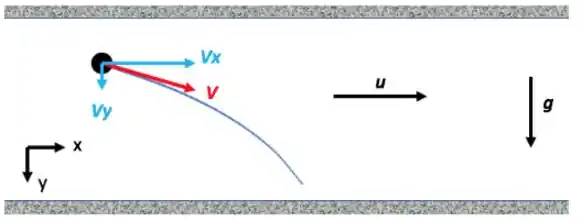
Bora entrar com a matemática agora. Lá no capítulo de velocidade terminal, chegamos na equação do movimento de uma partícula:
Lembrando que:
Mas a partícula tem movimento tanto no em como em . Bora escrever essa equação separadamente pra cada eixo, adaptando ao caso que estamos analisando, que é , já que sabemos que na Terra tem gravidade e o problema ninguém falou nada de campo centrífugo.
Agora entram aquelas hipóteses que eu falei lá no começo:
- Estamos desprezando a fase acelerada do movimento da partícula, daí as derivadas das velocidades (que são termos da aceleração) valem zero
- Se o movimento do fluido é unidimensional e dissemos, lá no desenho, que o fluido se move na direção de , ele só tem . A componente vale zero
- E, pelo desenho, gravidade, , está em apenas
Simplificando:
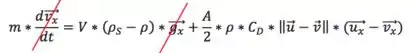
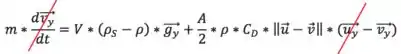
Reescrevendo essas duas últimas equações:
Vamos olhar cada uma delas separadamente; a primeira só pode ser zero de duas formas:
- , para que , mas isso sabemos que não pode ser verdade pela física problema mesmo. Repara no desenho, está na completamente na horizontal e não; vetores só são iguais se tiverem iguais direção, sentido e módulo; já vimos que direção e sentido não são iguais então nem vou me preocupar com módulos
- Só sobra a segunda opção, que é . Daí, acabamos de descobrir que na direção do escoamento, fluido e partícula se movem com a mesma velocidade
Agora, antes de olhar pra segunda equação, bora lembrar de álgebra linear. É assim que calculamos o módulo de um vetor qualquer de componentes :
Daí, calculando o módulo de , ou seja, :
Como . Além disso, já vimos que . Daí:
Agora, substituindo por na segunda equação e o isolando:
E essa é a expressão que achamos pra velocidade terminal de partícula sedimentando em fluido parado, com ,lá no tópico de velocidade terminal. Ou seja: . Resumo da ópera:
Conclusões:
- Na direção do escoamento, fluido e partícula caminham com a mesma velocidade
- Na direção do campo, a partícula caminha com velocidade terminal
Partícula suspensa em um fluido confinado em recipiente em rotação
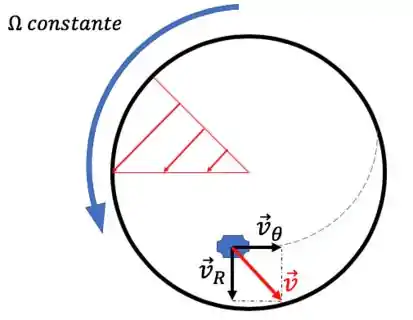
As hipóteses aqui são as mesmas do caso anterior:
- Escoamento unidimensional do fluido
- Vamos desprezar a fase transiente do movimento da partícula
Também precisamos “considerar” algumas coisas:
- Estamos vendo um recipiente de raio e em , ou seja, bem no centro, a partícula não tem translação, mas tem sim ROTAÇÃO. Isso pode parecer algo meio óbvio de falar, mas falei porque em mecânica dos fluidos a gente vê alguns casos (imaginários) dessa partícula no centro parada e isso alteraria o perfil de velocidades
- Vamos considerar velocidade angular constante
- E, por fim, vamos considerar que , isto é,
Começando com a matemática: nesse caso, é conveniente usarmos NÃO os eixos cartesianos mas sim coordenadas radial e angular . Escrevendo as componentes de e :
Escrevendo as duas componentes da equação do movimento:
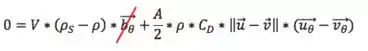
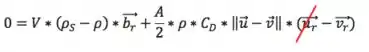
Da primeira tiramos que , ou seja, na direção do movimento do fluido, a partícula se move com a mesma velocidade que o fluido.
Agora, vamos ver o , que nem fizemos no primeiro caso que vimos:
Voltando com isso pra equação do movimento:
Essa expressão aí é a da velocidade terminal para campo centrífugo, , ou seja, .
Conclusões:
- Na direção do escoamento, fluido e partícula caminham com a mesma velocidade
- Na direção do campo, a partícula caminha com velocidade terminal
Repara que a partícula vai se aproximando da parede do recipiente já que tem uma velocidade em direção à ela, no sentido do campo centrífugo.
Lembrando que o campo centrífugo é radial e para fora:

Pra fechar o tópico, quero só que você repare uma coisa:
- No campo gravitacional , é constante independentemente de que “ponto dentro do escoamento” você analise.
- Já no campo centrífugo , é proporcional a .
Partícula suspensa em um fluido confinado em recipiente em rotação
Exercícios Resolvidos
Exercício Resolvido #1
Elaboração própria
Descreva o movimento de uma partícula em um fluido em movimento unidirecional na horizontal apenas com palavras.
Dado: o movimento do fluido é perpendicular ao campo gravitacional e este é o único campo atuando.
Passo 1
Temos um fluido em movimento unidirecional na horizontal. Bora imaginar que ele está se movendo no eixo X partindo da origem e indo e direção ao sentido positivo do eixo. Bora também adotar esse sentido como sendo pra direita:

Embora o fluido esteja se movendo apenas no sentido positivo do eixo X, o movimento da partícula tem que ser avaliado em todo o espaço, isto é, nos três eixos.
Como vimos na teoria:
- Na direção do escoamento, fluido e partícula caminham com a mesma velocidade
- Na direção do campo, a partícula caminha com velocidade terminal
Ou seja:
- No eixo x a partícula caminha com a mesma velocidade que o fluido e também no sentido positivo do eixo.
- No eixo y a partícula caminha com velocidade terminal. Adotando o sentido do eixo y como positivo para baixo, sabemos que a partícula caminha nesse sentido já que a gravidade também aponta para baixo.
- Adotando o eixo z como indo “para os lados” do movimento do fluido, sabemos que o movimento da partícula é zero nesse eixo pois não há nenhuma força motriz para tal.
Resposta
Ei, a resposta está no passo a passo :)
Exercício Resolvido #2
Elaboração própria
Utilize agora equações de conservação para descrever o movimento de uma partícula em um fluido em movimento no sentido positivo do eixo x. Sabe-se que a gravidade aponta para baixo e perpendicular ao movimento do fluido.
Passo 1
Já vimos no exercício anterior que “para os lados” do movimento do fluido a partícula não se movimenta, ou seja, todo o movimento da partícula está concentrado nos eixos x e y, conforme definido abaixo:
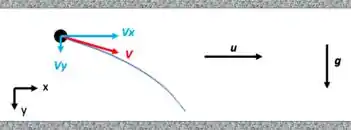
Daí, nem vou me preocupar com esse “terceiro” eixo. A partícula apenas apresenta velocidade nos eixos x e y.
Como o enunciado pede pra usarmos equações de conservação pra descrever o movimento, entra a matemática. Vamos precisar usar a equação do movimento da partícula:
Repara que já coloquei , já que o único campo de forças atuando é o gravitacional.
Como há movimento em dois eixos, abrimos essa equação para os dois eixos, x e y:
Passo 2
Com as hipóteses de:
- Escoamento unidimensional do fluido
- Desprezando a fase transiente do movimento da partícula
Vamos simplificar as equações:
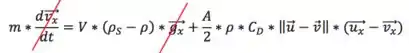
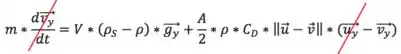
Dessa forma, ficamos com:
Olhando pra primeira equação, como vimos na na teoria, essa multiplicação só pode ser zero se
Já que sabemos que já que igualdade de vetores implicaria igualdade de módulo, direção e sentido, e sabemos (até pelo desenho mesmo) que isso não ocorre; esses dois vetores NÃO têm mesmas direção e sentido.
Então, já provamos que na direção do escoamento, fluido e partícula caminham com a mesma velocidade:
Passo 3
Olhando para a segunda equação que chegamos:
Calculando o esse módulo que aparece:
E já sabemos que daí
Além disso, , já que o fluido apenas se movimento no eixo x. Portanto:
Agora, substituindo por na segunda equação e o isolando:
Já igualei à pois esta é a expressão que achamos pra velocidade terminal de partícula sedimentando em fluido parado, com ,lá no tópico de velocidade terminal. Ou seja, provamos que na direção do campo, a partícula caminha com velocidade terminal:
Resposta
Ei, a resposta está no passo a passo :)
Exercício Resolvido #3
Elaboração própria
Explique, com palavras apenas, como é o movimento de uma partícula confinada em um recipiente em rotação. Considere que o campo centrífugo é bem maior do que o campo gravitacional e que a velocidade angular do recipiente é constante.
Passo 1
Bora lá. Primeiro de tudo, o enunciado fala pra considerar que campo centrífugo é bem maior do que o campo gravitacional, daí, é como se o campo gravitacional nem existisse, podemos desprezá-lo.
Temos que olhar para todas as componentes do movimento da partícula. Para esses casos de rotação, é conveniente pensarmos em coordenadas cilíndricas. Podemos dividir o movimento da partícula em:
- Movimento na direção do escoamento
- Movimento na direção do campo
O que vimos na teoria é que:
- Na direção do escoamento do fluido, a partícula caminha com a mesma velocidade que o fluido. Como o movimento do fluido é na direção angular, podemos dizer que:
- Já na direção do campo centrífugo, que aponta para fora sempre e no sentindo radial, vimos que a partícula caminha com velocidade terminal.
Já no terceiro eixo das coordenadas cilíndricas, eixo Z, do comprimento, NÃO há movimento da partícula pois não há nenhuma força motriz para tal.
Resposta
Ei, a resposta está no passo a passo :)
Exercício Resolvido #4
Elaboração própria
Utilize equações de conservação para descrever o movimento de uma partícula confinada em um recipiente em rotação. Considere que o campo centrífugo é bem maior do que o campo gravitacional e que a velocidade angular do recipiente é constante.
Passo 1
É a mesma coisa do exercício anterior, mas agora temos que usar equações de conservação para chegar nas mesmas conclusões.
O enunciado fala pra considerar que campo centrífugo é bem maior do que o campo gravitacional, daí, é como se o campo gravitacional nem existisse, podemos desprezá-lo. E, pela geometria do problema, é conveniente utilizar coordenadas cilíndricas.
Lembrando as componentes de e :
Repara que eu ignorei as componentes em Z porque sabemos que não há nenhuma força motriz para movimento nesse eixo.
Como o enunciado pede pra usarmos equação de conservação, vamos usar a equação do movimento:
E como há movimento em dois eixos, vamos ter que avaliar essa equação para cada um dos eixos.
Para o movimento angular:
Já para o movimento na direção radial, do campo:
Passo 2
Desprezando a fase transiente do movimento (já que é muito rápida), podemos cortar as derivadas no tempo.
Além disso, sabemos que o campo centrífugo é apenas radial então podemos dizer que:
E, considerando que o movimento do fluido é unidirecional, apenas angular:
Dessa forma, as equações ficam:
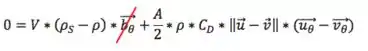
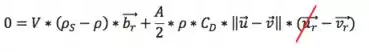
Da primeira tiramos que , ou seja, na direção do movimento do fluido, a partícula se move com a mesma velocidade que o fluido. Uma parte do movimento já provamos.
Para avaliar a segunda, precisamos do valor de :
Voltando com isso pra equação do movimento no eixo radial:
Já igualei essa raiz à velocidade terminal pois, como vimos, essa é a expressão para
velocidade terminal com campo centrífugo, . Ou seja, achamos que na direção do campo:
Resposta
Ei, a resposta está no passo a passo :)
Exercício Resolvido #5
Elaboração própria
Desprezando-se a fase transiente do movimento, que é, em geral, muito rápida quando se fala de partículas, partículas caminham com velocidade terminal na direção do campo de forças a que estão submetidas (mesmo se essa não for a única componente de seu movimento). Entretanto, há uma diferença na velocidade terminal se esse campo de forças for gravitacional ou centrífugo. Diga qual é essa diferença e explique o porquê de sua existência.
Passo 1
Essa é uma diferença muitoooo importante. É tipo a cereja do bolo quando se fala em escoamento, então não vai esquecer, ok?
Quando o escoamento ocorre submetido ao campo gravitacional , o campo é constante e por isso a velocidade terminal é constante!
Já para entender o que ocorre quando a partícula está submetida ao campo centrífugo, precisamos avaliar a fórmula do campo centrífugo:
Em que:
Repara que quando o campo de forças é centrífugo ele NÃO é constante; vemos que ele é linearmente dependendo do raio, .
Escrevendo a expressão da velocidade terminal para :
Notamos que é diretamente proporcional a quando o campo é centrífugo.
Resposta
Ei, a resposta está no passo a passo :)
Exercício Resolvido #6
Elaboração própria
Imagine um equipamento de separação infinitamente longo, isto é, cujo comprimento é muito maior do que a altura e largura.
Um fluxo de partículas suspensas em um gás é introduzido no equipamento, estando estas dispersas ao longo de toda a área transversal do equipamento.
Sabendo que o equipamento está submetido ao campo gravitacional apenas e este é perpendicular ao fluxo, onde você esperaria encontrar maior concentração de partículas na saída do equipamento, em termos de área transversal da saída, considerando que as partículas NÃO fiquem retidas no equipamento e a área transversal do equipamento seja constante?
Passo 1
O enunciado fala um bando de coisa, mas bora organizar tudo:
- Temos um equipamento muitoooo longo, então é como se houvesse tempo infinito pra tudo acontecer dentro dele
- Há partículas em suspensão na entrada do equipamento
- Há campo gravitacional perpendicular ao fluxo
Queremos saber onde haverá maior concentração de partículas na saída do equipamento e, para isso, temos que lembrar lá da teoria: na direção do escoamento, partículas caminham com velocidade igual a do fluido e, na direção do campo, caminham com velocidade terminal.
Passo 2
Na direção do escoamento, partículas caminham com velocidade igual à do fluido, daí sabemos que as partículas vão sair do equipamento, já que estamos considerando a NÃO retenção de partículas no equipamento.
Na direção do campo, partículas caminham com velocidade terminal, daí, tendem a atingir a parte debaixo do equipamento, o “chão” do equipamento.
O lance é que, como o equipamento é infinitamente longo, haverá tempo suficiente para tudo que tiver que acontecer, de fato acontecer. Ou seja, partículas de fato chegarão no chão do equipamento.
Passo 3
Já vimos que partículas vão sair do equipamento e vao se chegar ao chão do equipamento, já que equipamento é infinitamente longo. Daí, em termos de área transversal da saída, partículas se concentrarão na parte mais baixa da saída, no “chão” da saída.
Resposta
Partículas se concentrarão na parte mais baixa da saída, no “chão” da saída.