Velocidade Terminal
Produzido por Marcelo AlvesTeoria
Fala aí! Bora conversar sobre velocidade terminal?!
A velocidade terminal é a velocidade atingida por um objeto em queda livre no momento em que sua aceleração é nula, isso é, a somatória das forças que atuam nele é igual a zero.
Para calcular a velocidade terminal usamos a seguinte fórmula:
Onde:
é o volume da partícula; é a massa específica da partícula; é a massa específica do fluído; é o campo de força que esta atuando na partícula, pode ser por exemplo, a gravidade ou uma força centrípeta; é a área projetada da partícula; é o coeficiente de arrasto.
-Hãam?? Que?? 😵💫😵💫😵💫
Calma! Fica comigo que você vai entender como chegamos na fórmula da velocidade terminal, o que significa cada variável e como usamos essa fórmula!
Se liga nesse vídeozinho com tudo o que você precisa saber sobre velocidade terminal! 👇
Ou continua comigo no textinho! 😉
Introdução à Dinâmica da Partícula
Precisamos antes de qualquer coisa, entender alguns conceitos! Pra começar, vamos imaginar uma partícula qualquer em queda livre! Qual a força
Existem dois tipos de forças importantes na nossa análise: forças de campo
Forças de Campo
As forças de campo atuam independentemente de contato. Na nossa análise, as forças de campo que vamos ter de considerar são peso e empuxo. A força peso atua na direção e sentido da gravidade enquanto o empuxo atua em sentido oposto. Daí, para uma partícula sedimentando em um fluido:
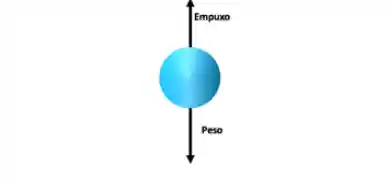
Matematicamente, podemos escrever:
Substituindo a massa:
Mas escrevemos essa expressão supondo que a partícula está sob atuação do campo gravitacional, por isso consideramos a gravidade. Porém, ela pode estar imersa em um campo de força diferente, então, bora generalizar. Vamos usar a letra
Forças de Superfície
A força de superfície é dividida em duas outras forças, a força de arraste
Acontece que, em sistemas particulados, a força de arraste é muito maior que a força de sustentação. Daí:
-“Mas qual a expressão da força de arraste?”
Calmaaa. É isso que vamos ver agora : )
Coeficiente de Arraste
Vimos esse
O coeficiente de arraste é dado por:
Onde:
é a força de arraste; é o diâmetro da partícula; é o módulo da velocidade relativa entre fluido e partícula ; é a massa específica do fluido;
Os termos
O
O
Podemos calcular o número de Reynolds da partícula com a seguinte fórmula:
Mas quando formos usar o
A equação do movimento da partícula
Pela Segunda lei de Newton o somatório de forças externas
Mas a aceleração é a derivada da velocidade em relação ao tempo, logo ficamos com:
Como,
Já vou jogar com
A expressão de
Entendendo Melhor a Velocidade Terminal
E, finalmente, chegamos em velocidade terminal!
Como falamos lá em cima, a velocidade terminal é a máxima velocidade que a partícula pode realmente atingir na sua sedimentação; é uma velocidade constante e, portanto, associada a uma aceleração zero!
-“Mas porque isso ocorre? Por que a velocidade não aumenta infinitamente?”
A resposta pra isso é força de arraste! Conforme a partícula ganha velocidade, a força de arraste aumenta; isso vai acontecendo até que o somatório das forças atuando sobre a partícula vai a zero e, como
Se liga nesse esqueminha:
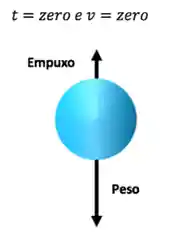
No esquema acima temos uma partícula sedimentando em um fluido parado, então
Quando o tempo é maior que zero, a partícula já está em movimento e, por isso, surge a força de arraste. Entretanto, antes de atingida a velocidade terminal, ainda há aceleração uma vez que ainda há força resultante
Repara que essa força resultante aponta pra baixo já que a velocidade está aumentando pra baixo, ou seja, a aceleração aponta pra baixo.
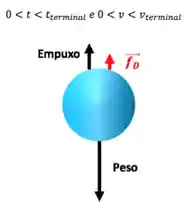
Quando
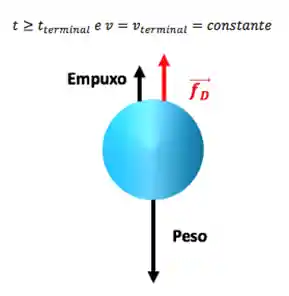
Algo bem útil e importante é saber que os tempos para as partículas atingirem a velocidade terminal são, geralmente, bem curtos.
Então, provavelmente sempre, vamos desprezar a fase acelerada do movimento e considerar que a partícula se move com velocidade terminal (a partir de agora, vamos chamar de
Fórmula da Velocidade Terminal
Considerando a equação de
Vamos considerar o fluido parado, então
Isolando o
Aweee! Chegamos na fórmula da velocidade terminal!
Agora podemos praticar com exercícios!
Introdução à Dinâmica da Partícula
Coeficiente de Arraste
A equação do movimento da partícula
Entendendo Melhor a Velocidade Terminal
Exercícios Resolvidos
Exercício Resolvido #1
Mostre as forças atuando sobre uma partícula sedimentando em cada um dos casos abaixo:
- Partícula sob ação de campo gravitacional sedimentando imersa em um fluido parado
- Partícula sob ação de campo gravitacional sedimentando no vácuo absoluto
Passo 1
Antes de qualquer coisa, estou colocando essa questão aqui porque caiu uma igualzinha na minha prova quando fiz essa disciplina haha.
Esse exercício não quer nada muito complexo, é só fazer um desenho das forças atuando na partícula em cada um dos casos.
Para a partícula sedimentando num fluido parado, é igualzinho ao que vimos na teoria.
Já pra partícula no vácuo, temos que ter mais atenção! Como ela está em vácuo absoluto, NÃO vai ter nem empuxo e nem força de atrito, arraste! Isso porque o empuxo é uma força sim relacionada com o campo gravitacional, mas que só existe quando o corpo está imerso em um fluido. Já o atrito, surge do choque do corpo com partículas do meio em que ela está sedimentando, mas como está no vácuo, não tem essas partículas do meio então não há choques que gerem atrito.
Passo 2
- Partícula sob ação de campo gravitacional sedimentando imersa em um fluido parado
Para uma partícula sob ação de campo gravitacional sedimentando imersa em um fluido parado, temos o mesmo caso que vimos na teoria.
- Por estar sob ação do campo gravitacional, vai aparecer a força peso.
- Por estar imersa em um fluido e sob ação do campo gravitacional, aparece o empuxo.
- Por estar com uma velocidade não nula em um meio contendo “algo” (repara que aqui eu estou me referindo às partículas do fluido, moléculas do fluido... e não às partículas que estão sedimentando) vai ter força de arraste
- Partícula sob ação de campo gravitacional sedimentando no vácuo absoluto
- Por estar sob ação do campo gravitacional, vai aparecer a força peso.
- Por NÃO estar imersa em um fluido, NÃO há empuxo.
- Por NÃO haver choques com a partícula sedimentando uma vez que não há nada no caminho dela (está no vácuo, né?), NÃO haverá força de arraste.
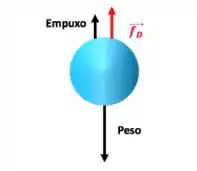
Temos que desenhar essas setinhas então elas têm que ter algum tamanho. Eu sei que lá da Física a gente aprende que tamanho está relacionado ao módulo, mas ignora isso nesse exercício, ok? Não temos nenhuma informação pra avaliar os módulos dessas forças nesse exercício então simplesmente desenhe e seja feliz haha.
Passo 3
Foi aquilo que discutimos lá no passo 1, se está em vácuo absoluto, não há empuxo e nem força de atrito. Vai ter apenas a força peso, devido ao campo gravitacional.

Resposta
Ei, a resposta está no passo a passo :)
Exercício Resolvido #2
Elaboração própria
Sobre a velocidade terminal de uma partícula sedimentando em um líquido parado, classifique as afirmativas em verdadeiras ou falsas. Justifique sempre.
- Mudar o material que compõe a partícula não alteraria sua velocidade terminal
- A aceleração é máxima quando
- Considerando densidade constante, quanto maior a partícula, maior será sua velocidade terminal
Passo 1
O objetivo dessa questão é fixar bem os conceitos teóricos desse capítulo. Vamos precisar bastante deles daqui pra frente.
Bora lá, temos o caso de uma partícula sedimentando num fluido parado e três afirmativas sobre velocidade terminal pra analisar. Já que vamos falar de velocidade terminal, é bom ter a fórmula dela ao nosso lado. Pela equação do movimento, chegamos em:
Em que é o volume da partícula e é sua área projetada.
Passo 2
- Mudar o material que compõe a partícula não alteraria sua velocidade terminal
- A aceleração é máxima quando
- Considerando densidade constante, quanto maior a partícula, maior será sua velocidade terminal
Ao mudar o material, estaríamos alterando a densidade dele, . Vemos, pela fórmula, que a densidade do material está sim relacionada com a velocidade terminal e alterá-la afetaria sim a velocidade terminal.
Como está no numerador, aumentar aumentaria e, da mesma forma, se diminuir diminui . Um exemplo pra isso são partículas de e partículas de ouro, de mesmo tamanho e no mesmo fluido. Como a densidade do ouro é maior, do ouro é maior, para um mesmo diâmetro de partícula.
Passo 3
Epa! Falsa! Quando o somatório de forças externas atuando na partícula é nulo e, pela segunda lei de Newton:
Daí se , a aceleração tem que ser nula . O que é máximo quando é o módulo da velocidade, que vai ser constante.
Passo 4
Olha de novo pra fórmula da velocidade terminal:
Não tem nenhum diâmetro aparecendo ainda, mas bora lá: o volume a gente expressa em , ou seja, unidade de comprimento ao cubo. Já a área, é em unidade de comprimento ao quadrado. A unidade de comprimento que usamos pra partículas é algum diâmetro equivalente, né. Vamos falar diâmetro , agora. Daí, vai ser proporcional a:
Repara que eu não usei “” e sim o “proporcional” porque não sabemos qual a constante que acompanha essas potências de diâmetros já que nada foi nos dito sobre a morfologia. Simplificando os :
Daí, vemos que o diâmetro fica no numerador. A afirmativa é verdadeira porque quanto maior o tamanho da partícula, maior vai ser seu diâmetro e maior será .
Resposta
- Falsa
- Falsa
- Verdadeira
Exercício Resolvido #3
Elaboração própria
Mostre matematicamente que é possível explorar a velocidade terminal para separar partículas de iguais tamanho e morfologia imersas em um mesmo fluido e que diferem apenas no material.
Suponha constante.
Passo 1
Basicamente, essa questão está perguntando se partículas de iguais tamanho e morfologia imersas em um mesmo fluido e que diferem apenas no material têm velocidades terminais diferentes.
O que vou fazer é chamar uma partícula de 1 e outra de 2 e escrever as velocidades terminais delas, de forma genérica:
Repara que eu chamei a densidade da 1 de e a da 2 de . Vou considerar que 1 é a mais densa, ou seja, .
Agora, vamos comparar essas duas velocidades. Vou escrever uma do lado da outra e, como ainda não sei se essas velocidades são , vou colocar uma interrogação entre elas. O objetivo do problema vai ser determinar qual sinal matemático a interrogação é.
Passo 2
Vamos buscar formas de simplificar o problema, ver o que é constante, jogar pra fora da raiz e sair cortando coisas dos dois lados.
Primeiro de tudo, tanto a área projetada como o volume podem ser escritos como uma constante (que depende da morfologia da partícula) vezes uma potência do diâmetro. Para o volume, essa constante é o fator de forma ; para a área projetada, não tem nenhuma constante específica, então bora dizer que essa constante é .
Agora começamos a cortar as coisas haha:
- Se as partículas têm a mesma morfologia: e
- Se as partículas têm o mesmo tamanho:
- Estando as partículas no mesmo fluido, estamos com iguais
- Nada foi falado sobre diferentes campos de força em cada caso, daí é um só
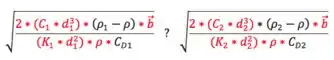
Cortei tudo que era igual, mas repara que não podia cortar esse do numerador porque ele tá dentro de um parêntesis então não tenho como tirar ele da raiz pra cortar. O enunciado diz para assumir constante, daí:
Como e é igual:
Daí:
Ou seja, provamos que quanto mais densa (maior ) a partícula, maior a velocidade terminal dela.
Passo 3
“Mas, Marcelo, o enunciado diz que é pra ser assumido constante...por que você não cortou logo ele junto com os outros?” Só porque quero comentar um pouco mais sobre eles com você haha. O que a questão pediu já acabou lá no passo 2.
Vimos lá na teoria que depende de e , isto é, . Como a morfologia é igual nos dois casos, sobra apenas pra analisar. A fórmula do é
Escrevendo pras duas partículas:
Já vimos que e os diâmetros são iguais:
Assumindo constante, vimos que , daí:
Um spoiler do próximo capítulo é que conforme aumenta, ou diminui ou fica constante; nunca aumenta. Ou seja, quem tiver velocidade terminal maior teria menor , já que estamos avaliando todos outros termos do iguais e iguais. Daí, voltando pra:
Como , e os estão no denominador, o lado esquerdo poderia ficar maior ainda.
E pra que eu falei isso tudo do ? Pra você NÃO pensar que ficaria tipo um cabo de guerra entre e . O que acontece, na verdade, é que eles vão por mesmo lado: se aumenta, diminuir, contribuindo pra aumentar.
Resposta
Ei, a resposta está no passo a passo :)
Exercício Resolvido #4
Elaboração própria
Imagine duas partículas idênticas imersas em um mesmo fluido estagnado. Sem nada pra fazer, as duas partículas resolveram apostar corrida. Sabendo que as partículas estão expostas a campo de força centrífugo apenas e cada uma está exposta a um campo de mesma direção e sentido, mas intensidades diferentes, qual das duas partículas ganhará a corrida?
Despreze a fase acelerada do movimento e considere que o coeficiente de arrasto é igual para as duas partículas.
Passo 1
Que louco! Duas partículas disputando corrida haha Mas deixa elas lá né, fazer o que? Haha
Bora focar no que interessa: quem ganhará a corrida? O enunciado manda desprezar a fase acelerada do movimento, daí, consideramos que, desde o início, partículas caminham com velocidade terminal. Como vimos lá na teoria, a expressão pra velocidade terminal em fluido estagnado é:
Agora, temos duas partículas, então vamos ter que comparar as velocidades delas. A que tiver maior velocidade, ganhará a corrida.
Passo 2
Olhando, novamente, pra expressão da velocidade terminal:
Bora destacar, em vermelho, tudo que for igual nas duas partículas:
- Partículas são idênticas, daí iguais e
- Enunciado fala pra considerar iguais coeficientes de arrasto, isto é,
- Como o fluido é o mesmo, iguais
Daí:
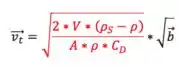
Ou seja, nessas condições, a diferença de velocidade depende apenas do campo. Quem tiver maior campo terá maior velocidade terminal e ganhará a corrida.
Resposta
Nessas condições, a diferença de velocidade depende apenas do campo. Quem tiver maior campo terá maior velocidade terminal e ganhará a corrida.
Exercício Resolvido #5
Elaboração própria
Determine a razão entre os campos centrífugos 1 e 2, isto é , tal que as velocidades terminais das partículas 1 e 2 sejam as mesmas. Sabe-se que as partículas 1 e 2 são esféricas, de mesmo material e 2 possui o dobro do diâmetro de 1. Ambas estão imersas num mesmo fluido, estagnado, e cada uma está exposta, exclusivamente, aos campos centrífugos e , respectivamente. Considere o coeficiente de arraste, , igual para as duas partículas.
Passo 1
Resumindo o enunciado, temos duas partículas de mesmo material (daí igual ), mas de tamanhos diferentes; em termos de diâmetros, é dito que:
As duas partículas estão imersas em um mesmo fluido (daí igual ), mas expostas a campos centrífugos distintos, e .
O enunciado pede pra considerarmos igual para as duas partículas e, a partir disso, achar a razão para que a velocidade terminal das duas partículas seja igual.
Sem dúvida, vamos ter que trabalhar com a expressão de para sedimentação em fluido estagnado, que vimos lá na teoria:
Como as partículas são esferas: e , lembrando que é o volume e é a área projetada. Daí, substituindo:
Passo 2
Agora que já sabemos com qual expressão vamos trabalhar, bora começar a escrever a expressão pra cada uma das esferas:
Usando :
Passo 3
Temos que achar a razão para que a velocidade terminal das duas partículas seja igual. Opa! Velocidades iguais... esse vai ser nosso ponto de partida, bora igualar essas duas velocidades.
Agora, vou colocar em evidência tudo que for igual para as duas:
E o que for igual podemos cortar dos dois lados, né? Daí:
Elevando os dois lados ao quadrado:
E, como queremos a razão :
Bom lembrar que, para que as velocidades terminais sejam iguais, os campos devem estar atuando na mesma direção e sentido 😉