Introdução - Método Mc-Cabe Thiele Gráfico
Produzido por Marcelo AlvesTeoria
Introdução
Finalmente chegamos no cálculo do número de pratos da nossa coluna!!! O Método Mc-Cabe Thiele gráfico é um método aproximado para calcular isso, e é mais preciso quanto maior for a idealidade do sistema estudado.
Esse método possui a vantagem de usar apenas balanço de massa, então não precisamos pensar em termos de energia. Além disso, ele utiliza os diagramas de equilíbrio que já vimos, de composição de líquido por vapor.
Antes da gente começar a mostrar as deduções para entender esse método, vou falar uma regra desse método que costuma fazer a galera perder ponto em muita questão de prova:
SEMPRE utilize vazões molares para as vazões da corrente. O Mc-Cabe Thiele só é válido assim, ok!?!
Vou falar aqui para você algumas coisas que assumimos quando usamos esse método:
- Vazão molar constante dentro de uma seção da coluna.
- Entalpia/Calor de Vaporização constante dentro de uma seção.
Bora analisar as seções!!
Análise da Seção de Topo
Bem, eu já te falei que para esse método vamos usar basicamente balanços de massa, né? No entanto, não vão ser os balanços de massa da coluna inteira, a gente vai olhar para cada seção dela separadamente.
Então, vamos pegar a nossa coluna e olhar apenas para uma seção, ok? Bora fazer uma envoltória nela.
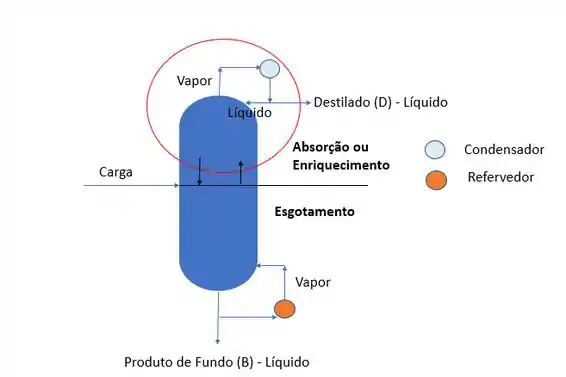
Vimos que para fazer balanço de massa precisamos considerar tudo que entra e tudo que sai da região que estamos analisando, certo?
Então, nesse caso vemos que está entrando o vapor () que está subindo e está saindo o líquido ( que está descendo, além do produto de topo (). Logo, nosso balanço de massa global fica assim:
E o nosso balanço por componente, vai possuir o seguinte formato:
Repara que usamos a nossa notação de sempre, onde fração molar da fase vapor é e vazão molar da fase líquida é .
Se a gente dividir os dois lados por , obtemos que:
Então, repara que agora nossa equação parece muiiito com uma reta do tipo . E aonde vamos aplicar essa equação? Nos nossos diagramas de equilíbrio , conforme a próxima figura.
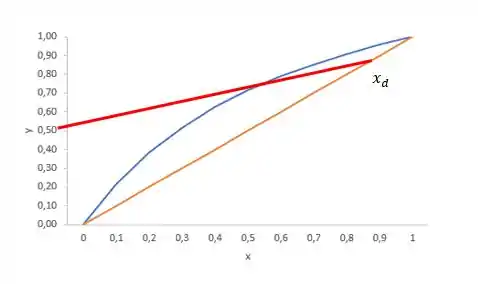
Para o exemplo acima, utilizamos .
Para traçar nossa reta, precisamos de, ao menos, dois ponto. Quando , . E o ponto “final” e quando , ou seja, pegamos e marcamos esse ponto na diagonal. Isso acontece pois o líquido e vapor no condensador total tem a mesma composição, afinal todo vapor se transforma em líquido. Então e podemos traçar nossa reta partindo da diagonal.
Outra coisa, como estamos considerando todas as vazões como molares, a gente pode dizer que dentro de uma mesma seção a vazão não muda. Portanto, vamos chamar de e de para toda a seção de absorção.
Só que essa equação também pode ser escrita em função da nossa razão de refluxo, pois . E, como vimos que , obtemos que:
Dividindo tudo por :
Substituinto :
Lembrando que essa é a razão de refluxo externa de topo!
Essas equações que obtemos, tanto usando a razão de refluxo quanto deixando em função das vazões, são equivalentes. Elas recembem o nome de Reta de Operação da Seção de Absorção ou ROSA.
Análise da Seção de Esgotamento
Por analogia ao que mostramos antes, agora vamos fazer o balanço de massa (novamente!), mas numa envoltória considerando o fundo da coluna. E se antes a gente obteve a ROSA, agora vamos obter a ROSE, ou seja, Reta de Operação da Seção de Esgotamento.
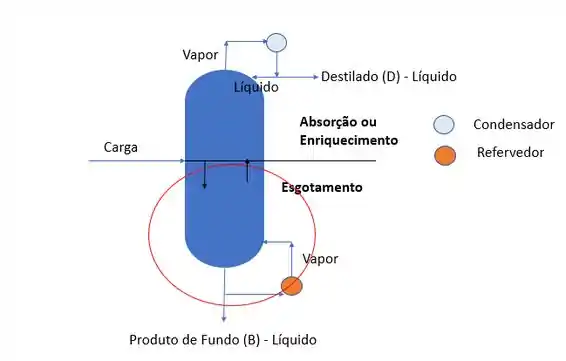
Nesse caso, o produto e o vapor estão saindo da envoltória e o líquido está entrando.
E o balanço de massa por componente fica:
Se isolarmos o e dividirmos tudo por também chegamos numa equação semelhante a equação da reta:
Vamos reescrever simplificando a notação? vai ser a vazão de líquido para a seção de esgotamento, enquanto que o vapor vamos denotar como para o esgotamento também.
Podemos escrever essa equação também em função da razão de refluxo de fundo e ela fica com esse formato aqui:
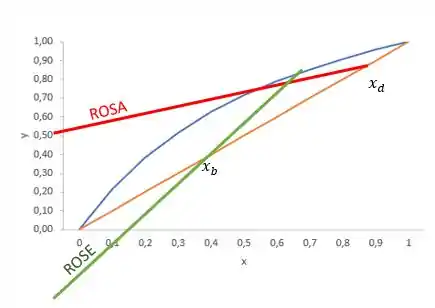
E vamos marcar ela no gráfico da mesma forma que fizemos para a outra, considerando que o nosso é por exemplo.
Análise da Carga
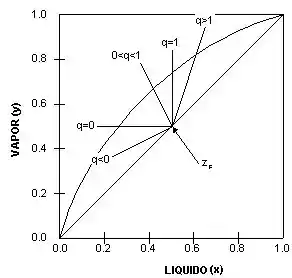
Outra forma de sabermos onde essas retas vão se cruzar, é utilizarmos as retas para a carga que já vimos. A inclinação dessa reta depende do tipo de carga que está sendo alimentada, lembram?
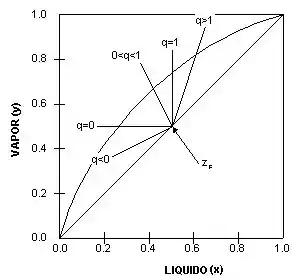
Então, vamos utilizar como exemplo uma carga alimentada com e que seja um vapor saturado (reta q horizontal em laranja). Vamos representar essa reta no nosso gráfico junto da ROSA.
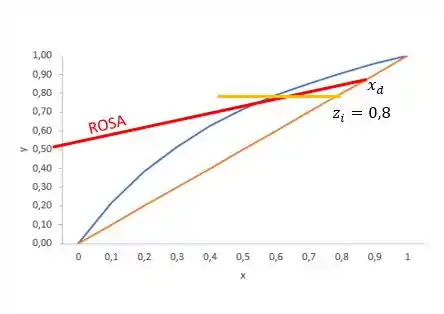
O ponto de interseção entre a rosa e a reta de carga delimita aonde a ROSA acaba e começa a ROSE. Portanto, como conhecemos o , podemos apenas ligar o até esse ponto para encontrar nosso ROSE.
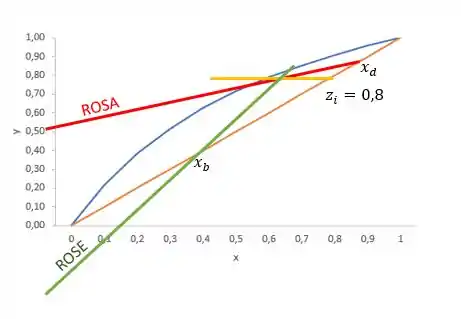
O gráfico obtido tem que ser o mesmo nos dois casos, ok?
Encontrando o número de estágios
Agora para fechar esse tópico, vamos descobrir como encontrar o número de estágios!
Para isso, vamos precisar fazer o seguinte:
- Traçar uma reta horizontal de até a nossa curva de equilíbrio
- Quando tocar a cuva de equilíbrio vamos traçar uma reta vertical até a nossa reta de operação
- Repetir os procedimentos 1 e 2 até que as linhas que estamos desenhando cruzem a reta q, indicando que houve a troca de seção
- Repetir os procedimentos 1 e 2, mas utilizando a nova reta de operação como referência
- Finalizar quando a reta que estamos desenhando ultrapassar a composição do produto de fundo!
No nosso exemplo, fica assim ó:
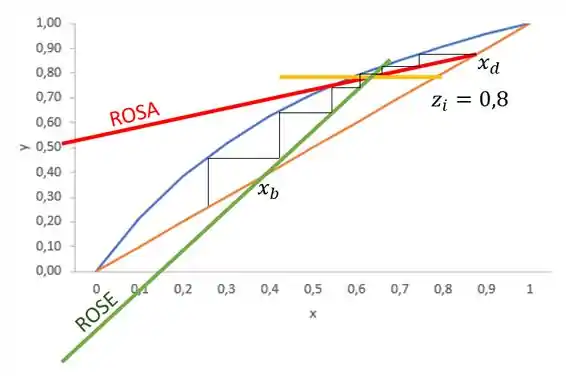
Portanto, quantos estágios nós temos? Nós contabilizamos o estágio através do número de vezes que a nossa “escadinha” toca a curva de equilíbrio. Portanto, nesse caso temos 6 estágios.
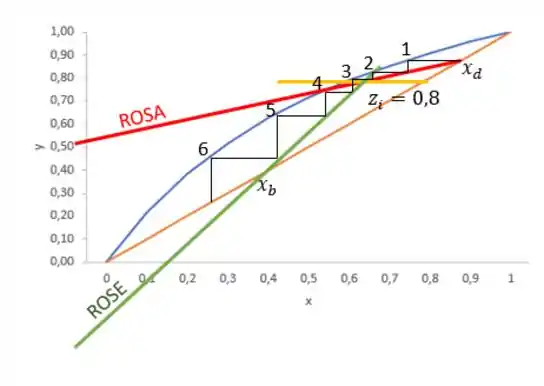
Só mais uma coisa! Ali no estágio 3 estamos cruzando a nossa reta , né? Então vamos chamar esse prato como prato ótimo de carga. A composição desse prato é igualzinha à composição da carga, ok?
Atenção com uma coisa muiiito importante:
Número de estágios e de pratos não são a mesma coisa!
Se uma coluna tiver um refervedor total e um condensador total, o número de estágios e de pratos serão iguais. No entanto, se algum deles for parcial, essa unidade (condensador ou refervedor) representa um estágio de equilíbrio, pois nesses equipamentos temos o equilíbrio de líquido e vapor.
Logo, se você encontrar no seu gráfico 6 estágios e sua coluna tiver um condensador parcial, você só tem 5 pratos. O 6º estágio é o condensador. Se ela tiver condensador parcial e refeverdor parcial, ela só terá 4 pratos, pois o primeiro e último estágios são o condensador e refervedor, respectivamente.
Análise da Seção de Esgotamento
Análise da Carga
Encontrando o número de estágios
Exercícios Resolvidos
Exercício Resolvido #1
Adaptado Concurso Público – Nível Superior – INMETRO
O metodo de McCabe-Thiele é bastante utilizado para avaliação do comportamento de misturas binárias em colunas de destilação. Em relação ao método de McCabe-Thiele, julgue as afirmativas a seguir.
- Admite a operação com fluxos variáveis das correntes de líquido e vapor nas seções da coluna.
- O método admite variação das entalpias de vaporização dos componentes da mistura.
- A volatilidade relativa também é determinante para o projeto da coluna. Nesse sentido, quanto maior for o valor de volatilidade relativa, maior será o número de pratos da coluna
Passo 1
Quando começamos a estudar o método Mc-Cabe Thiele, vimos algumas considerações que eram feitas:
- Vazão molar constante dentro de uma seção da coluna.
- Entalpia/Calor de Vaporização constante dentro de uma seção.
Potanto, já podemos dizer que as letras A e B são falsas. Bora avaliar a letra C!!!!
Passo 2
A letra C se refere à volatilidade relativa. No método Mc-Cabe Thiele, de fato usamos a volatilidade relativa!
Se a volatilidade relativa é grande, é mais fácil separar um composto entre a fase líquida e vapor, portanto a nossa coluna vai ser mais simples e possuirá um menor número de pratos. Logo, a alternativa C também é falsa!
Resposta
A, B e C são falsas.
Exercício Resolvido #2
Concurso Petrobras – 2018- Engenheiro de Processamento Júnior
Um método bastante utilizado para estudo de destilação é o McCabe-Thiele, em que a resolução gráfica permite determinar diversos parâmetros da coluna de destilação. Nesse método, a reta delimita as retas de retificação e o esgotamento para a condição de uma determinada coluna.
Além de efetuar a separação entre áreas dentro do destilador, a reta :
a) descreve a condição da alimentação e do prato respectivo.
b) indica quando se têm misturas azeotrópicas.
c) determina o número de pratos mínimos.
d) determina as condições de operação da zona de retificação.
e) determina os parâmetros do condensador do destilador.
Passo 1
Bem, essa questão aí é sobre a importância da nossa reta . Ela pode parecer boba, mas é super importante para entender o funcionamento da nossa coluna.
A reta , para a coluna de destilação com uma seção de absorção e uma de esgotamento, marca no gráfico aonde mudaremos de seção. Portanto, ela separa as áreas dentro do destilador, conforme a questão informou.
Além disso, a única outra opção dessas aí que pode ser atribuída à reta é determinar a condição de alimentação e do prato respectivo. Afinal, a inclinação dela dava o estado físico da carga!
Portanto, nossa resposta é letra A (A de amor por Operações Unitárias )!
Resposta
Letra A
Exercício Resolvido #3
Elaboração própria
Determine a razão de refluxo do sistema abaixo:
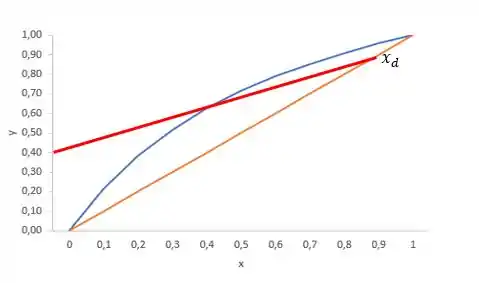
Passo 1
Nessa questão, precisamos determinar a razão de refluxo através do gráfico que foi dado. A primeira coisa que precisamos pensar é que essa reta aí vermelha é a nossa Reta de Operação da Seção de Absorção, a famosa ROSA. E nós já conhecemos a equação da ROSA:
Passo 2
Beleza, mas como usamos isso para achar a nossa razão de refluxo? Então, a ROSA não é nada além de uma equação da reta. Portanto, se a gente souber ou o coeficiente linear ou o coeficiente angular, podemos encontrar a razão de refluxo.
No nosso gráfico, tá tranquilo de ver que o coeficiente linear é , lembrando que o coeficiente linear é onde a nossa reta corta o eixo .
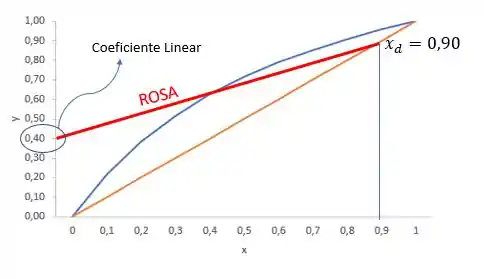
Portanto, como sabemos que (ponto onde a ROSA “acaba”, cruzando a nossa diagonal) conseguimos calcular a nossa razão de refluxo, por:
Logo, obtemos que :
Uma observação muito importante é que essa razão de refluxo não é a que de fato vamos utilizar na operação. Nos próximos tópicos, vamos explicar com mais detalhe as várias classificações de razão de refluxo que podem existir 😊
Resposta
Exercício Resolvido #4
Adaptado Concurso CESPE – INMETRO – Área: Metrologia Química
A figura a seguir corresponde ao diagrama de McCabeThiele de uma mistura binária processada em uma coluna de destilação. Os valores correspondem à composição, em porcentagem da quantidade de matéria do componente mais volátil na mistura líquida () e na fase vapor ().
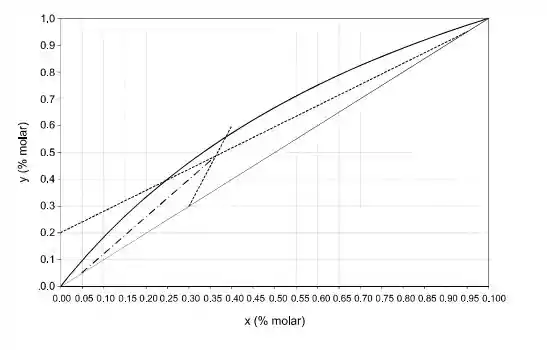
Indique as composições, em porcentagem de quantidade de matéria do componente mais volátil nas correntes de alimentação, de topo e de fundo da coluna de destilação, e a razão de refluxo no topo da coluna.
Passo 1
Essa questão pede várias coisas para a gente! A primeira coisa que vamos fazer é identificar o que é cada reta nesse gráfico!
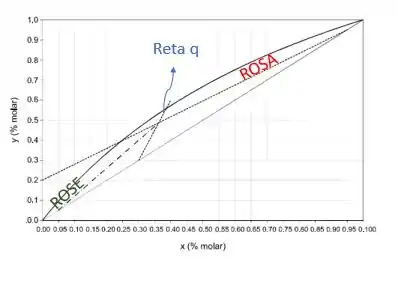
Passo 2
Vamos começar avaliando o topo da nossa coluna.
Sabemos que a ROSA termina bem na composição do produto de topo, certo? Portanto, vamos efetuar a leitura dessa composição no gráfico, ok?
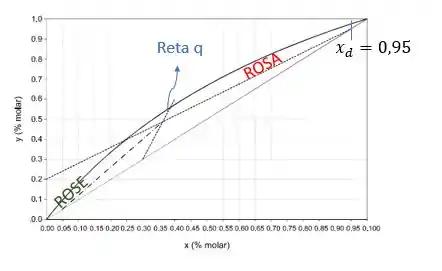
Então, o nosso produto de topo possui do componente mais leve, já que é ele que sai em maior proporção no topo!
Passo 3
Da mesma forma que podemos ver a composição de topo pelo fim da ROSA, podemos ver a composição de fundo pelo fim da ROSE.
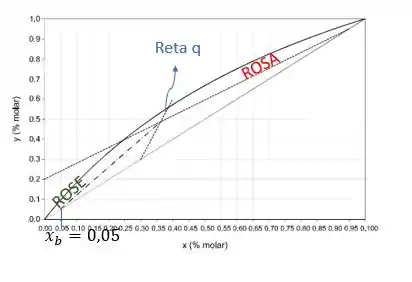
Por aí vemos que a composição do produto de fundo é , o que faz total sentido, pois o fundo é mais rico no componente mais pesado (menos volátil) e mais pobre no componente mais volátil.
Passo 4
Para saber a composição da carga, precisamos olhar para a nossa reta . O local onde a reta se inicia, ou seja, toca a diagonal , será o ponto onde veremos a composição da carga .
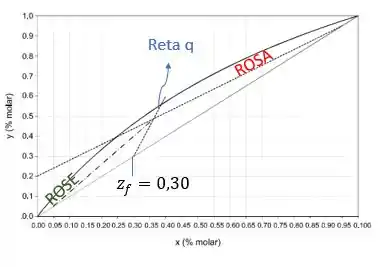
Portanto, a composição da carga é .
Passo 5
A última coisa que precisamos é determinar a razão de refluxo. E para isso, podemos usar o coeficiente linear da nossa ROSA (lembrando que ROSA é a Reta de Operação da Seção de Absorção). E nós já conhecemos a equação da ROSA:
Nesse caso, o coeficiente linear é .
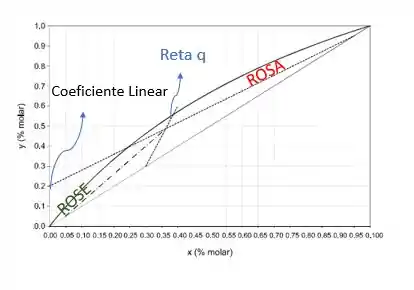
Portanto, como sabemos que , conseguimos calcular a nossa razão de refluxo, pois:
Logo, obtemos que :