Análise de Elementos
Produzido por Marcelo AlvesTeoria
Variáveis de Projeto
Chegou a hora de começar a pensar na infinidade de coisas que podemos projetar! Colunas de flash, de destilação, extração... Como podemos fazer isso? Quantas variáveis precisamos conhecer? Quais propriedades precisamos saber?

Bem, para responder isso vamos precisar fazer umas continhas.
Independentemente do projeto, algumas variáveis devem sempre ser avaliadas. Elas são: temperatura, pressão, composição, vazão e repetição. Eu sei que nem todas elas são óbvias, mas já já vamos ver na prática como utilizá-las!
Apesar de um sistema ter várias variáveis, nem sempre precisamos conhecer todas, pois, muitas vezes, já existem algumas restrições que são naturais. E com essas restrições podemos cortar o número de informação que serão necessárias.
Então, vamos chamar de o número de variáveis que precisam ser informados em um equipamento para que ele esteja totalmente caracterizado. E esse pode ser calculado da seguinte forma:
Ou seja: é o número de variáveis totais () menos o número de restrições ().
Existem vários tipos de restrições: restrição inerente, restrição de balanço de massa, restrições de balanço de energia, restrição de equilíbrio de fases e de equilíbrio químico (quando estivermos considerando reações). Para os equipamentos que estamos estudando aqui, não consideramos reações, então vamos ignorar as restrições de equilíbrio químico.
Vamos aplicar isso em exemplos para entender o funcionamento, beleza?
Análises de Elementos –Tubulação
Ao invés de analisar logo de cara uma coluna de destilação ou de extração inteirinha, vamos dividir nossos equipamentos em vários pedacinhos. Assim as coisas ficam mais simples e depois basta juntar todos esses pedacinhos pra montar um equipamento mais complexo!
Então bora começar analisando uma tubulação. Pensa em uma mistura com componentes escoando dentro de uma tubulação.

Quais seriam as variáveis para estudar em uma tubulação?
Temperatura, pressão, composição e vazão certamente seriam os itens que mais influenciariam. Mas o número de variáveis não é 4. Pensa aqui comigo: para a temperatura, basta conhecer seu valor; para a pressão e a vazão, também. Agora, para a composição já é um pouquinho diferente, pois precisamos saber a composição em relação a todos os componentes que estão ali.
Então, como nossa mistura tem componentes, a gente precisa saber a concentração de componentes. Se você tiver se perguntando o motivo de precisarmos conhecer apenas dados de composição, calma aí que eu vou explicar.
Se tivermos, por exemplo, uma mistura de água, metanol e etanol, ou seja, 3 componentes (). Caso saibamos que a fração de água é e de metanol é , a fração de etanol será , pois a soma das frações de todos os componentes deve ser um. Então, eu precisei apenas de duas informações (), e com isso já caracterizamos completamente a composição da corrente.
Então o nosso número total de variáveis é:
Temperatura
Pressão
Vazão
Composição
Logo, para uma tubulação!
Agora vamos avaliar as restrições. Numa tubulação pela qual os componentes estão apenas passando, não precisamos nos preocupar com balanço de massa, energia e nem nada. Então o
Com isso, conseguimos obter o número para tubulação:
Se nosso é igual a 3, por exemplo, isso indica que precisamos de 5 informações! Podem ser por exemplo, temperatura, pressão... e por aí vai.
Análises de Elementos –Divisor de Fluxo
O próximo elemento é o divisor de fluxo. Vamos avaliar a divisão de uma corrente A em duas correntes, B e C.
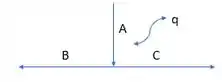
Se a gente for reparar, nesse caso é como se tivéssemos três tubulações (A,B e C). Então, como temos três correntes, podemos “colar” do número que calculamos antes, beleza?
Nosso vai ser dado por:
Esse “” aí apareceu porque, no nosso divisor de fluxo, podemos ter entrada ou saída de calor ().
E quais seriam as nossas restrições? Se estamos apenas dividindo o fluxo de A entre B e C, B e C devem ter as mesmas temperatura e composição. Porém, A e B (ou C) também precisam ter a mesma composição. Então, nossas restrições são:
Igualdade de temperatura e pressão entre B e C , pois é para temperatura e para pressão.
Igualdade de composição entre B e C , pois lembra que não precisamos saber de todos os componentes!
Igualdade de composição entre A e B
Balanço de energia
Balanço de massa global
Então:
Logo:
Análise de Elementos – Misturador
O misturador é super parecido com o divisor de fluxo, só que ao invés de separar as correntes, elas vão ser unidas.
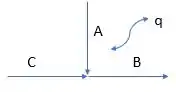
Então, o vai ser igualzinho ao do separador:
Já número de restrições vai mudar um pouquiiinho. Repara que, nesse caso, não podemos dizer que as correntes que estão se juntando terão a mesma temperatura, pressão e composição. Então, nossas únicas restrições serão balanço de massa por componente, balanço de massa global e balanço de energia.
Balanço de massa por componente
Balanço de massa global
Balanço de energia
Assim:
E:
Análise de Elementos – Bombas, Aquecedores e Resfriadores
Beleza, nessa nossa próxima análise de elementos vamos fazer um como exemplo e os outros serão análogos ok? Bombas, aquecedores e resfriadores possuem os mesmos , e .
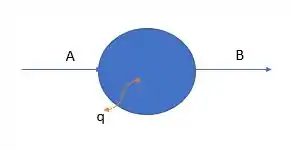
Temos duas correntes envolvidas e uma possibilidade de entrada/saída de calor, então:
E as restrições são:
Balanço de massa por componente
Balanço de massa global
Balanço de energia
Assim:
E:
Análise de Elementos – Condensadores, Refervedores Totais e Parciais
Para condensadores e refervedores (totais ou parciais), temos basicamente três correntes envolvidas e temos um dispositivo de adição/remoção de calor. Abaixo, coloquei uma representação bem genérica.
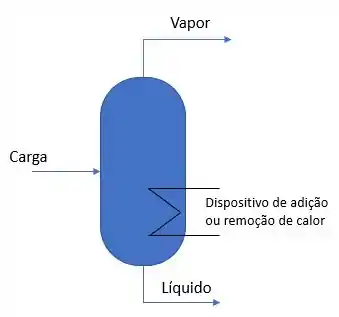
Então, temos o . As restrições que já vimos para esse caso são balanço de massa e balanço de energia. No entanto, temos que adicionar uma restrição referente ao líquido e vapor que saem do dispositivo, pois eles estão em equilíbrio e então devem ter mesma temperatura e pressão. Além do equilíbrio de fases entre todos os componentes... Lembram do e ?
As restrições vão ser:
Balanço de massa por componente
Balanço de energia
Balanço de massa global
Restrição inerente entre líquido e vapor (igualdade de temperatura e pressão)
Relação de equilíbrio de fases
Portanto, nosso .
Análise de Elementos – Estágio de Equilíbrios
Vimos que em colunas de destilação temos vários estágios de equilíbrios. Nesses estágios, temos as correntes de líquido e de vapor que entram e saem, totalizando 4 correntes. Além disso, temos também o dispositivo de adição/remoção de calor.
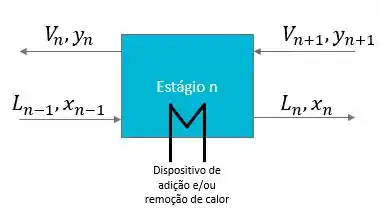
Logo, nosso . Mas temos que avaliar também as nossas restrições.
Temos que ter igualdade de temperatura e pressão entre as correntes que deixam o estágio, os balanços de massa por componente e global, balanço de energia e as relações de equilíbrio entre as fases líquido e vapor para todos os componentes. Então, vamos ver essas restrições!
Balanço de massa por componente
Balanço de energia
Balanço de massa global
Restrição inerente entre líquido e vapor (igualdade de temperatura e pressão)
Relação de equilíbrio de fases
Portanto, nosso .
Análise de Elementos – Estágio de Equilíbrios de Carga
Se o estágio que vimos anteriormente fosse um estágio de carga, teríamos uma corrente a mais entrando, tendo um total de 5 correntes. E as restrições em relação ao estágio de equilíbrio que vimos anteriormente não mudariam.
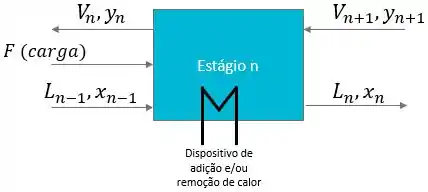
Então, nosso número de variáveis seria:
E o número de restrições não muda, logo:
Como resultado, teríamos:
.
Análise de Elementos – Estágio de Equilíbrios com Retirada de Produto
Se ao invés de uma entrada no estágio de equilíbrio, tivermos uma saída, vamos observar a seguinte configuração.
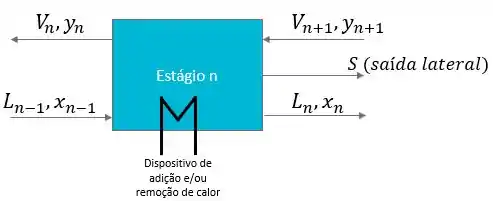
O número de variáveis será o mesmo que o obtido anteriormente para estágios com carga (), pois temos o mesmo número de correntes e o mesmo disposivito para remoção/adição de calor. No entanto, as restrições mudam, pois agora precisamos considerar que temos 3 correntes saindo em equilíbrio e não mais duas apenas.
As restrições passam a ser:
Balanço de massa por componente
Balanço de energia
Balanço de massa global
Restrição inerente entre líquido e vapor (igualdade de temperatura e pressão)
Relação de equilíbrio de fases
Igualdade de composição entre a retirada e a outra corrente saindo no mesmo estado físico
Igualdade de temperatura e pressão entre a retirada e a outra corrente saindo no mesmo estado físico
Vamos aos cálculos:
Logo:
Análise de Unidades
E para fechar, eu sei que esse tópico tá sendo super longo e cansativo, mas vamos ver como juntar tudo isso?
Numa coluna de destilação, por exemplo, vamos ter vários estágios de equilíbrio, certo? Então, não vamos recalcular os vários que aprendemos a calcular. Ao invés disso, vamos ver quais elementos que constituem o equipamento.
Então, se eu tenho uma coluna com 10 estágios, eu vou ter que considerar 10 vezes as variáveis dos estágios e vou precisar também levar em consideração que eu tenho uma coisa apenas que está se repetindo (que é o número de estágios). Isso significa que se eu tivesse um processo com 2 bombas e 4 estágios, eu ia precisar considerar as repetições deles para o número de variáveis, mas também ia precisar saber que tenho duas coisas que estão se repetindo, a bomba e o estágio!
E como consideramos isso tudo? A partir da seguinte fórmula:
Onde é o número de equipamentos que eu estou avaliando e esse indica que estamos fazendo o cálculo de uma unidade, ou seja, de um conjunto de elementos. E o número de restrições é aquele que já estávamos acostumados, só tendo cuidado para não contar uma mesma restrição entre dois estágios diferentes, pois a corrente que sai de um estágio está entrando em outro, para o caso de múltiplos estágios.
E:
Então nós vimos como calcular tanto para elementos quanto para unidades. Isso significa que já podemos “montar” unidades através de elementos e calcular os desses carinhas!
Análises de Elementos –Divisor de Fluxo
Análise de Elementos – Misturador
Análise de Elementos – Bombas, Aquecedores e Resfriadores
Análise de Elementos – Condensadores, Refervedores Totais e Parciais
Análise de Elementos – Estágio de Equilíbrios
Análise de Elementos – Estágio de Equilíbrios de Carga
Análise de Elementos – Estágio de Equilíbrios com Retirada de Produto
Análise de Unidades
Exercícios Resolvidos
Exercício Resolvido #1
Exemplo Caderno Operações Unitárias 2 - UFRJ
Faça análise do número de variáveis e restrições de um estágio de equilíbrio (sem carga ou retirada lateral), sabendo que esse estágio de equilíbrio é adiabático.
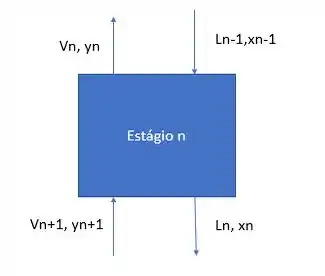
Passo 1
Para responder essa questão, vamos partir de uma análise que já vimos na teoria que mostra a representação de um estágio , que tem um dispositivo para adição/remoção de calor.
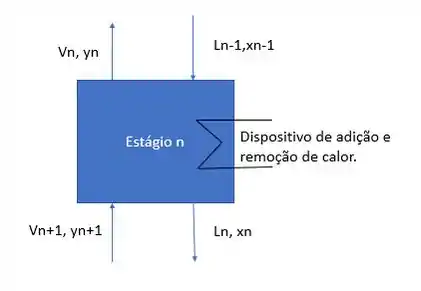
Como possuíamos 4 correntes e um trocador de calor, calculamos que o nosso era dado por:
No sistema que a questão pede para avaliar, temos também 4 correntes, mas não possuímos nenhum trocador de calor, logo não é necessário acrescentar no .
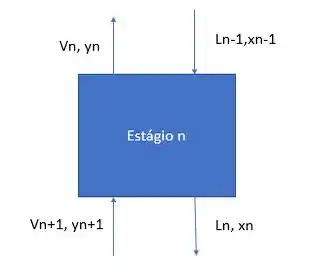
Portanto, o .
Passo 2
Bora avaliar também as nossas restrições!!
No sistema com aquecimento, vimos que temos que ter igualdade de Temperatura e Pressão entre as correntes que deixam o estágio, os balanços de massa por componente e global, balanço de energia e as relações de equilíbrio entre as fases líquido e vapor para todos os componentes. Então, vamos ver essas restrições!
Balanço de massa por componente
Balanço de energia
Balanço de massa global
Restrição inerente entre líquido e vapor (igualdade de temperatura e pressão)
Relação de equilíbrio de fases
Para o sistema sem aquecimento, não vamos ter mudança nenhuma nas nossas restrições, elas continuam exatamente as mesmas 😊
Passo 3
Agora, precisamos calcular nosso !
Substituindo:
Pronto, chegamos no nosso resultado!!!!
Resposta
Exercício Resolvido #2
Exemplo Caderno Operações Unitárias 2 - UFRJ
Faça análise do número de variáveis e restrições de um estágio que possua tanto carga quanto retirada de produtos. A representação desse estágio está disponível a seguir.
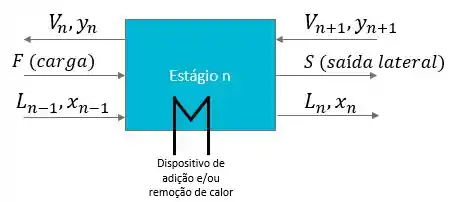
Passo 1
Beleza, vamos começar fazendo a análise das variáveis.
Temos 6 correntes e temos o dispositivo de adição/remoção de calor. Logo, nosso número de variáveis é:
Passo 2
Vamos para a análise de restrições. As restrições são:
Balanço de massa por componente
Balanço de energia
Balanço de massa global
Restrição inerente entre líquido e vapor (igualdade de temperatura e pressão)
Relação de equilíbrio de fases
Igualdade de composição entre a retirada e a outra corrente saindo no mesmo estado físico
Igualdade de temperatura e pressão entre a saída lateral e a outra corrente saindo no mesmo estado físico
Vamos aos cálculos:
Passo 3
E agora pro .
Substituindo tudo que achamos:
Portanto, é esse o nosso resultado 😊
Resposta
Exercício Resolvido #3
Elaboração própria
Considere a seguinte coluna de absorção com estágios. Faça a análise de variáveis e restrições dessa coluna.
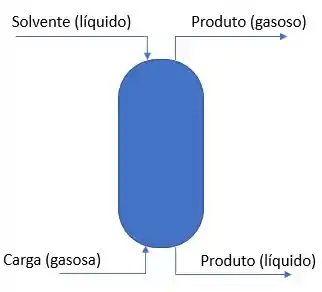
Passo 1
Primeiro, precisamos pensar que, quando falamos numa coluna de absorção, podemos ter diversos estágios. Como o número de estágios não foi especificado, vamos chamar de estágios.
Portanto, nesse caso, para fazermos a análise, precisamos considerar que estamos avaliando uma unidade, e não mais um elemento. O elemento nesse caso seria o estágio, só que como temos estágios se repetindo, precisamos usar a fórmula para as unidades.
Agora, nos próximos passos, vamos avaliar termo a termo dessas fórmulas, ok?
Passo 2
Nós vimos que para um estágio de equilíbrio qualquer (sem carga ou retirada), o .
Com isso, podemos calcular o nosso , pois .
Logo, como temos estágios, podemos dizer que:
E, como apenas os estágios de equilíbrio se repetem, nosso .
Assim:
Passo 3
O próximo passo é achar o , que está relacionado ao número de restrições. Repara que quando usamos para o estágio de equilíbrio, já consideramos as restrições que usamos quando fizemos essa dedução lá na teoria.
Então, quando estamos falando aqui de restrições, não estamos falando das restrições do elemento e sim das restrições da unidade.
Quando avaliamos um estágio, consideramos as 4 correntes envolvidas nele, então quando utilizamos esse para todos os estágios de forma igual, acaba que estamos considerando mais de uma corrente mais de uma vez. Isso ocorre, pois, com exceção do primeiro e do último estágio, toda corrente que sai de um estágio entra em outro.
Sabemos que as correntes que saem de um estágio devem ter mesma temperatura e pressão, como nessa próxima imagem aí:
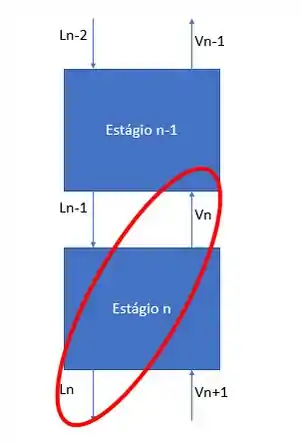
Então, o nosso número de restrições vai ser de duas correntes por estágio. Temos estágios, mas falamos sobre a duplicidade que ocorre no meio, então vamos considerar duas correntes em estágios.
Então, como já vimos que para uma corrente temos . Nesse caso, vamos ter:
Passo 4
Nosso último passo é o cálculo do .
Portanto:
E esse seria o número de variáveis que precisaríamos especificar.
Resposta
Exercício Resolvido #4
Elaboração própria
Realize a análise de variáveis de uma coluna de destilação simples com estágios. Considere que o condensador e o refervedor dessa coluna são totais.
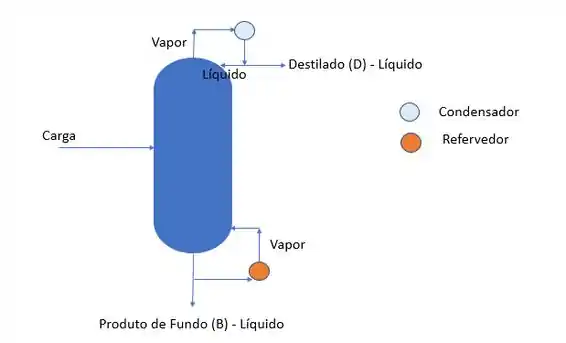
Passo 1
Primeiríssima coisa que precisamos fazer é uma análise dessa coluna de destilação para entender quais elementos estamos juntando nela!
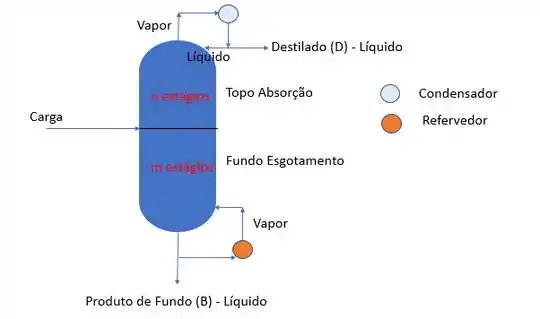
Nesse caso, acima da carga, temos estágios, que fazem parte da seção de absorção. E abaixo da carga, estágios que fazem parte do esgotamento.
Dessa forma, vamos dizer que o total são estágios, onde
Passo 2
Nós precisamos fazer a análise de uma unidade um pouquinho mais complexa do que fizemos antes, então vamos identificar todos os elementos. E, aproveitando, podemos preencher com os valores que colocamos para eles quando fizemos as deduções, beleza?
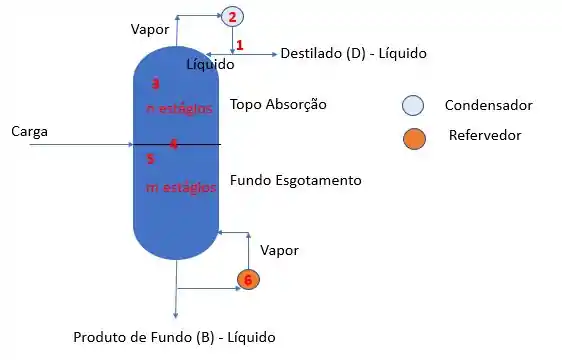
Vou colocar numa tabela para ficar mais organizado :P e depois explico caso a caso

Para o divisor de fluxo, condensador, refervedor total e estágio de carga apenas utilizamos os valores que mostramos durante a teoria 😊
Já para os estágios de absorção e esgotamento, precisamos fazer algumas considerações. A primeira delas é que, no outro exercício, vimos que para colunas de absorção o . No entanto, nesse caso temos uma parte para absorção e outra para esgotamento, e, portanto, precisamos fazer essa divisão usando ao invés de na absorção e ao invés de onde for esgotamento.
Além disso, na parte dos estágios de absorção, repara que colocamos , ao invés de . Fizemos isso, pois a soma de todos os estágios dessa coluna deve totalizar , e além do estágios de absorção/esgotamento, temos o estágio de carga, que precisamos deixar separado.
Portanto, tiramos um estágio da absorção na conta, e ele é considerado através da carga. Logo, temos estágios na absorção, na carga e no esgotamento. E isso totaliza .
Para finalizar, somando tudo, temos que:
Passo 3
Agora, vamos para as restrições dessa unidade 😊
Vamos considerar como restrição de uma unidade cada corrente que foi contada mais de uma vez. Então, por exemplo, quando consideramos o divisor de fluxo, a corrente que sai dele e entra na coluna é uma restrição! Pois ela é considerada tanto saindo do divisor quanto entrando no primeiro estágio da coluna.
Além disso, no estágio de carga, temos 4 restrições, pois todos as correntes que entram/saem dele também são consideradas nas entradas/saídas das seções de absorção e esgotamento!
Vamos marcar nossas restrições no desenho:
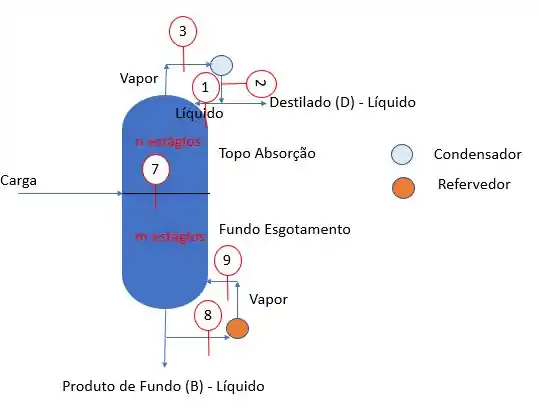
Portanto, temos correntes de restrições. Então .
Passo 4
Partindo para o cálculo de .
Logo:
Resposta
Exercício Resolvido #5
Lista de Exercícios Extra – Operações Unitárias 2 - UFRJ
Uma unidade separa uma mistura em 3 produtos (P1, P2 e P3) como mostra o esquema, determine:
- O número de variáveis
- O número de restrições
- O número de graus de liberdade
- As variáveis que podem ser especificadas.
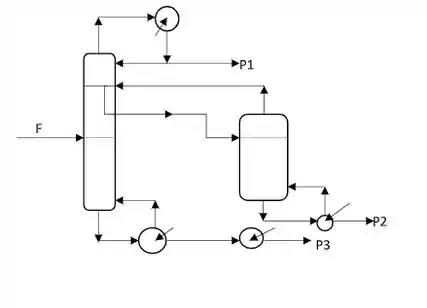
Passo 1
Primeira coisa que precisamos ver é o número de variáveis. Para isso, vamos identificar no desenho tudo que temos e fazemos uma tabela com os valores de de cada um deles, ok?
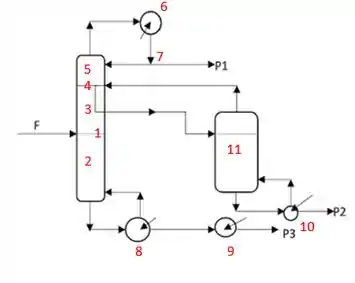
Colocando na nossa tabela:
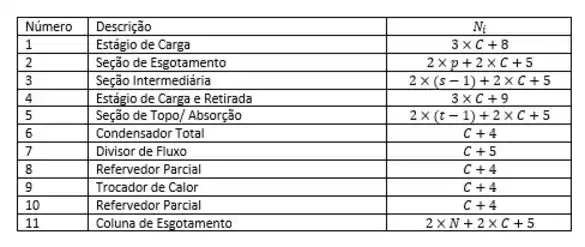
Observação: número de estágios da coluna de destilação, nesse caso, foi chamado de “P”. e foram os números de estágios em cada pedaço dessa coluna, de forma que . E o número de estágios da coluna de esgotamento, chamamos de .
Portanto, nosso já pode ser calculado, pois ele é o somatório de tudo que aparece na nossa tabela, beleza?
Passo 2
O próximo passo é a determinação das restrições. Vamos marcar elas conforme nossa contagem do número de restrições.
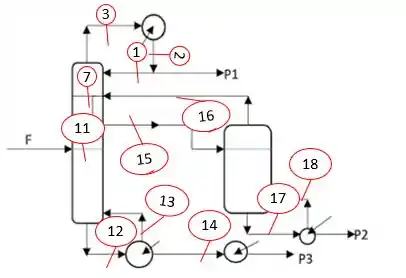
Temos 18 correntes de restrições, pois essas correntes estão sendo consideradas mais de uma vez quando fizemos a análise de variáveis. Lembrando que das restrições 3 para 7 e da 7 para 11, foi realizado o acréscimo de 4 correntes e não apenas de uma. Isso ocorreu, pois estamos falando de estágios com 2 correntes de entrada e 2 corrente de saída, totalizando 4 correntes, que estão sendo repetidas 😊 Portanto, precisamos acrescentar quatro restrições e não só uma!
Agora nosso já pode ser calculado. Ele vai ser o número de correntes que apresentam restrições vezes , que é o valor que calculamos para a restrição de uma corrente lá na teoria.
Passo 3
Próximo passo é o cálculo do
Assim:
)
Portanto, temos que:
Passo 4
Agora, para fechar essa questão, vamos ver o que podemos especificar, beleza?
Precisamos especificar informações.
Se a gente espeficar temperatura e pressão (2 informações) de cada estágio presente em e , teremos informações especificadas 😊
Agora, faltam apenas informações. Se a gente especificar a corrente de carga F, já podemos contar que temos mais informações especificadas.
Além disso, para fechar as 16 que vão ficar faltando, podemos definir razão de refluxo de topo (1 informação), temperatura e pressão dos produtos P1, P2 e P3 (6 informações), temperatura do refluxo do topo (1 informação) e temperatura e pressão dos 4 trocadores de calor/condensadores (8 informações).
Prontinho, são essas as informações que precisamos para deixar nossa unidade bem especificada.
Resposta
Temperatura e pressão de cada estágio presente em e ; corrente de carga F; razão de refluxo de topo; temperatura e pressão dos produtos P1, P2 e P3; temperatura do refluxo do topo; temperatura e pressão dos 4 trocadores de calor/condensadores.