Teoria
Introdução
Fala, galera! Chegou a hora de aprender a descrever o tamanho das partículas.

Se todas as partículas fossem esféricas, bastaria saber o diâmetro delas para saber o tamanho. Mas nem sempre são...

Ok. E se a partícula parecer um Mickey?

Relaxa que não vamos usar 30 milhões de parâmetros para descrever essa partícula.
"Então qual a solução?!" Vamos relacionar as partículas com esferas semelhantes, pegando alguma propriedade igual na partícula e nessa esfera equivalente. No final das contas, vamos dar um diâmetro equivalente para a partícula.
Bora ver melhor isso?
Diâmetro da esfera de mesmo volume que a partícula ()
Essa eu quero que você dê uma atenção especial, ok? É uma das mais importantes que vamos ver.
O que fazemos é medir o volume da partícula e igualar à fórmula do volume da esfera. Daí tiramos o famoso .
Talvez você tenha estranhado um pouco essa fórmula de volume da esfera (termo da direita). É porque geralmente gravamos como:
Mas a gente sabe que:
Se você substituir isso, chega naquela fórmula lá de cima.
Diâmetro da esfera de mesma área projetada que a partícula ()
A ideia aqui é a mesma do , mas vamos usar a área projetada agora. Daí:
Lembra que a área projetada de uma esfera é um círculo. Por isso esse termo da direita é a área de um círculo.
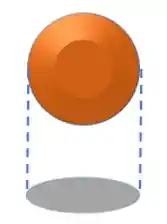
E ah, uma coisa importante: se a partícula não for simétrica, pegamos sempre a MAIOR área projetada, porque vai ser a configuração mais estável. Relaxa que nos exercícios você vai entender isso melhor.
Diâmetro da esfera com mesma área superficial ()
Repeteco! Mesma ideia, mas com área superficial da partícula:
Diâmetro de peneira ()
Esse daqui já é diferente. Ele é o diâmetro da esfera que passa sem folga pela malha de uma dada peneira.
“Oi? Como assim?”

Olha esse desenho que você vai entender melhor:
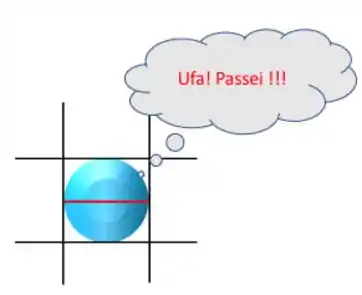
Como na horizontal o diâmetro de uma esfera ocupa toda a abertura da peneira, o vai ser a própria abertura da peneira.

Mas aí vem uma outra questão. Se a partícula passa por uma abertura de , por exemplo, significa que ela é menor do que esse tamanho. Mas menor quanto? Ela tem ,, ???
Para diminuir essa dúvida e restringir um intervalo de tamanhos, usamos duas peneiras de tamanhos diferentes.
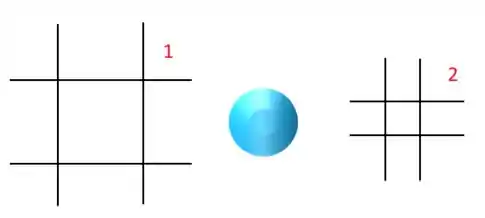
Usamos de forma que a partícula passe pela primeira peneira, mas fique retida na segunda. Depois, tiramos a média e dizemos que esse é o diâmetro de peneira médio ().
Diâmetro da esfera que sedimenta com mesma velocidade terminal que a partícula ()
Chegamos ao último :) O nome já diz quase tudo e parar chegar nessa fórmula podemos partir de uma das formas da Lei de Stokes.
Lembrando que é a intensidade do campo externo de forças, então considerando o campo gravitacional . Aquele é a densidade da partícula sólida e o é a densidade do fluido usado pra determinar a velocidade terminal.
Então, isolando o diâmetro, chegamos na equação do diâmetro!
Então toda vez que te pedirem para calcular o diâmetro de Stokes ou diâmetro da esfera de mesmo material que a partícula e que quando está nas mesmas condições atinge a mesma velocidade terminal, basta utilizar essa fórmula aí!
Relações entre diferentes diâmetros
E quando te pedirem para a partir de um diâmetro calcular outro? O procedimento normal seria usar as definições dos dois diâmetros para tentar fazer essa conta. Só que isso pode dar muiiiito trabalho!!!
Então, alguns professores permitem utilizar as relações entre esses diâmetros. Vamos ver as principais relações?
Existe uma relação muiiito importante entre e :
Outra que pode ser muito útil é entre e :
Por fim, temos essa aqui:
Diâmetro da esfera de mesmo volume que a partícula ( d V o u d p )
Diâmetro da esfera de mesma área projetada que a partícula ( d a )
Diâmetro da esfera com mesma área superficial ( d S )
Diâmetro de peneira ( d # )
Diâmetro da esfera que sedimenta com mesma velocidade terminal que a partícula ( d v t o u d s t k )
Relações entre diferentes diâmetros
Exercícios Resolvidos
Exercício Resolvido #1
Questão 1 a, Lista 1 Prof. Medronho UFRJ
Calcular a relação para um cubo.
Passo 1
É bom a gente sempre fazer um rascunho da geometria pra ajudar a gente, né? No caso de um cubo nem precisava, porque é bem simples. Mas bora fazer pra pegar o hábito, ok?
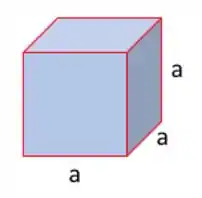
Passo 2
Vamos calcular o do cubo primeiro, que é o diâmetro da esfera de mesmo volume que o cubo. Precisamos do volume do cubo então, né?
Agora entramos com definição de :
Elevando os dois lados a , ou seja, aplicando raiz cúbica.
Passo 3
Agora precisamos calcular o, que é o diâmetro da esfera de mesma área projetada que nossa partícula, que nesse exercício, é o cubo.
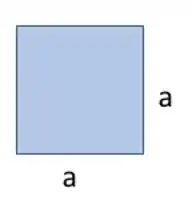
A área projetada de um cubo é um quadrado, certo? Pensa que você está olhando ele de frente.
Daí, calculando o :
Aplicando raiz quadrado dos dois lados:
Passo 4
O difícil já foi. Agora precisamos só dividir um pelo outro e achamos a resposta.
Cortando o “” em cima e embaixo e jogando essa galera na calculadora:
Resposta
Exercício Resolvido #2
Questão 1 b, Lista 1 Prof. Medronho UFRJ
Calcule a relação para um cilindro cuja altura é o dobro do diâmetro da base.
Passo 1
Primeiro de tudo, bora fazer um rascunho da geometria:
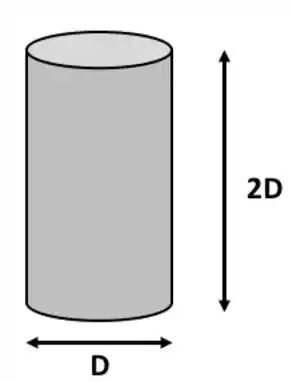
Passo 2
Vou começar calculando o e, para isso, vou precisar do volume desse cilindro aí.
Agora vamos aplicar a fórmula / definição de
:
Cortando os e isolando o :
Aplicando raiz cúbica dos dois lados:
Passo 3
Vamos agora calcular o . Para isso precisamos da área projetada do cilindro, certo?
Mas lembra que eu disse lá na teoria que pegamos sempre a maior área projetada!
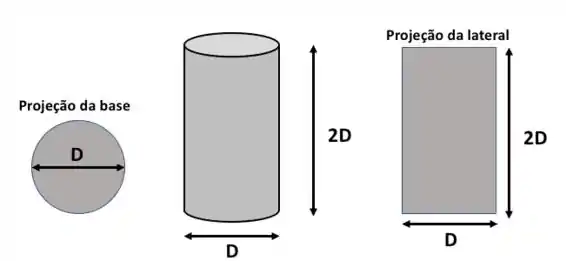
Como meu desenho tá em escala, já fica claro qual projeção é maior: projeção da lateral. Calculando as duas áreas vamos ver que é isso mesmo:
Daí vamos usar a área da projeção lateral:
Aplicando a fórmula / definição de o :
Passo 4
Agora é só dividir um pelo outro:
Cortando o “” em cima e embaixo e jogando o que sobrou na calculadora:
Resposta
Exercício Resolvido #3
Elaboração própria
Realizou-se a peneiração de uma amostra utilizando 3 peneiras, de aberturas iguais a , e . Entre as duas primeiras peneiras, obteve-se uma massa de partículas e, entre as duas últimas, uma massa . Pede-se os diâmetros médios de peneira das duas subfaixas.
Passo 1
A massa ficou retida entre as duas primeiras peneiras, ou seja, ela passou pela peneira de abertura , mas ficou retida na peneira de abertura .
Já a massa conseguiu passar pela peneira de abertura , mas ficou retida na de .
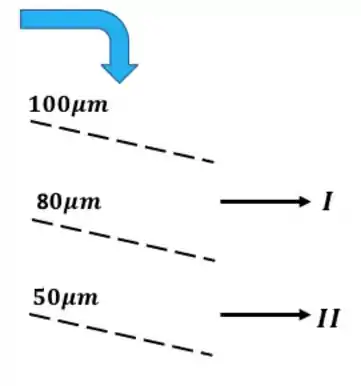
Os diâmetros de peneira () para cada uma das peneiras são a própria abertura delas.
Passo 2
Ok, já identificamos os diâmetros de peneira envolvidos no problema. Precisamos agora calcular os de cada uma das subfaixas.
Para a subfaixa :
Para a subfaixa :
Resposta
Exercício Resolvido #4
Elaboração própria
Um certo software analisa imagens, de partículas, obtidas com auxílio de um microscópio e uma câmera fotográfica.
Abaixo, tem-se um exemplo de imagem obtida.

Sabe-se que as partículas sempre estão na condição de maior estabilidade quando as imagens são capturadas.
O software calcula, para cada partícula analisada, o diâmetro de uma esfera equivalente.
Com as informações dadas, dentre os diâmetros equivalentes abaixo, qual é o único que o software é capaz de calcular?
Passo 1
Bora lá. O que importa pra gente do enunciado é que temos uma imagem 2D de partículas na condição de maior estabilidade, que é quando a área projetada delas é máxima.
Vamos avaliar letra por letra agora:
Passo 2
Para calcular o o software precisaria do volume das partículas, mas em nenhum momento esse volume foi dado, então não pode ser essa.
Passo 3
Para calcular o precisamos da maior área projetada da partícula. Opa! Mas é exatamente isso que temos.
A resposta é letra B, já achamos. Mas bora ver as outras alternativas.
Passo 4
Se quiséssemos calcular o , íamos precisar da área superficial total da partícula, mas não temos isso. Temos apenas uma imagem 2D de parte da partícula.
Passo 5
Em nenhum momento o enunciado falou sobre peneira, então não pode ser esse.
Passo 6
O enunciado não falou de velocidade terminal; apenas mostrou uma foto 2D das partículas.
Resposta
b)
Exercício Resolvido #5
Elaboração própria
Para uma partícula de alumina com o formato de um paralelepípedo com dimensões proporcionais a 7x5x2:
- Calcule e
- Sabendo que esta partícula será utilizada como catalisador em uma certa reação química, qual dos dois diâmetros é o mais indicado para descrever a partícula?
Dica: Lembre que uma catálise ocorre na superfície do catalisador.
Passo 1
Como as dimensões são proporcionais a 7x5x2, se uma dimensão vale 2L, por exemplo, as outras valem 5L e 7L.
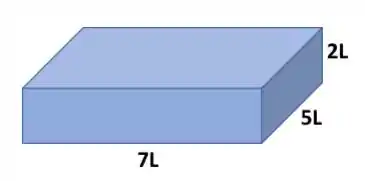
E ah, uma coisa, não faz diferença aqui se você tiver chamado a altura de 5L ou 7L ao invés do 2L, por exemplo, ok? A ordem não faz diferença.
Passo 2
Vamos, primeiro, calcular o e, para isso, precisamos do volume da partícula
Aplicando a definição de
Só um detalhe agora: esse enunciado não disse nada de unidade, né? Mas sabemos que diâmetro tem unidade de comprimento (u.c.), então, bora representar só pra evitar problema.
Passo 3
Precisamos agora calcular o , que é o diâmetro equivalente da esfera de mesma área superficial que a partícula.
A primeira coisa que vamos precisar, então, é da área superficial da nossa partícula. Como a nossa partícula é:
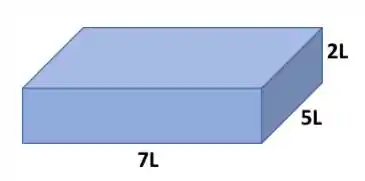
A área superficial dela vai ser:
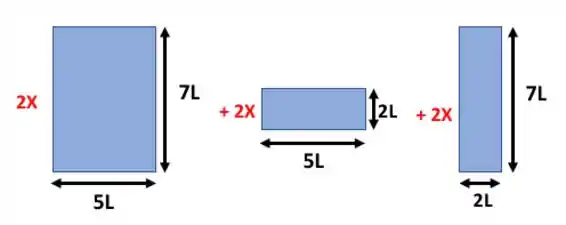
Escrevendo isso:
Aplicando agora a definição de :
Aplicando raiz quadrada dos dois lados:
Novamente, bora lembrar que diâmetro tem unidade de comprimento (u.c.), daí:
Passo 4
Agora o item b:
Sabendo que esta partícula será utilizada como catalisador em uma certa reação química, qual dos dois diâmetros é o mais indicado para descrever a partícula?
O enunciado diz que a partícula vai ser usada como catalisador e que catálises ocorrem na superfície do catalisador.
Daí, o diâmetro mais indicado é o , pois se relaciona com a área superficial da partícula e é isso que importa para nossa aplicação.
O que adianta sabermos o volume exato da partícula se o que importa para a gente é a área superficial?

Na teoria vimos 5 formas de comparar nossas partículas com esferas semelhantes, certo? Mas quando usa cada uma delas?
O ideal seria analisar a aplicação da partícula e ver o qual a propriedade se relaciona com aquela aplicação. Mas acaba que, na prática, muitas vezes usa-se o porque é mais fácil de medir experimentalmente.
Resposta
a)
b), pois é baseado na propriedade relacionada com a aplicação da partícula, área superficial, no caso.