Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Pêndulo de Torção

Ver Teoria
Exercício 7123456891011

Enunciado

Na vista superior da figura abaixo, uma barra longa e uniforme de massa M está livre para girar em um plano horizontal em torno do eixo vertical que passa pelo centro. Uma mola de constante elástica k   ligada horizontalmente entre uma das extremidades da barra e uma parede fixa. Quando a barra está em equilíbrio, fica paralela `a parede.

  1. Calcule o torque que a barra sofre quando é girada ligeiramente de um ângulo θ .
  2. Qual é o período das pequenas oscilações que acontecem quando a barra é girada ligeiramente depois liberada? (Dê a sua resposta em função da massa M e da constante de mola k .)

(Assume que o ângulo θ é pequeno o suficiente para que as aproximações s e n θ ≈ θ   e c o s θ ≈ 1 sejam válidas. Para uma haste fina e uniforme de massa M e comprimento L , o momento de inércia relativo a um eixo perpendicular à barra, passando pelo seu centro de massa, é I = M L 2 12 )

Passo 1

Fala galera, uma questão de MHS que busca conhecer o valor do torque que sofre a barra quando ela é girada. Inicialmente é legal a gente desenhar as forças que estão atuando na barra para termos uma melhor visualização do problema:

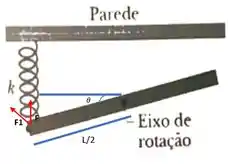
A componente da força restauradora, F 1 , pode ser dada como o produto da F   pelo c o s θ , onde F = - k y . Denotaremos y como o deslocamento da mola que será dado na direção vertical. Portanto: y = L 2 s e n θ .

Logo:

F 1 = - k L 2 s e n θ c o s θ

Temos que o torque é dado por:

τ = - F . L 2 = - k L 2 4 s e n θ c o s θ

∴

τ = - k L 2 4 θ .

Passo 2

A barra efetuará um MHS, onde o torque restaurador será dado por:

τ = - K θ = I d 2 θ d t 2

Onde:

K = k L 2 4 .

Vamos fazer:

τ = I d 2 θ d t 2 = - k L 2 4 θ

d 2 θ d t 2 = θ ¨

I θ ¨ + k L 2 4 θ = 0

Dividindo por I :

θ ¨ + k L 2 4 I θ = 0

Passo 3

Lembra da equação do MHS? Aqui ó:

x ¨ + ω 2 x = 0

Comparando, vemos que:

θ ¨ + k L 2 4 I θ = 0

ω 2 = k L 2 4 I  

Como I = M L 2 12 :

ω 2 = 3 k L 2 M L 2 = 3 k M

ω = 3 k M

E como:

T = 2 π ω

T = 2 π M 3 k

Resposta

A) τ = - k L 2 4 θ

B) T = 2 π M 3 k

Exercícios de Livros Relacionados

O balanço de um relógio antigo oscila com uma amplitude angular de πrad e um período de 0,500 s . Determine (a) a velocidade angular máxima do balanço, (b) a velocidade angular no instante em que o de
35. Um relógio da quatro tiques a cada segundo; cada tique corresponde à metade do período. A roda catarina do relógio consiste em uma fina camada circular com raio de 0,55c m conectada ao conjunto da
52.Um macaco mecânico de 1,80k g é suspenso por um pivô localizado a uma distância de 0,250m de seu centro de massa e começa a oscilar como um pêndulo físico. O período da oscilação com ângulo pequeno
13.6E Considere o pêndulo de torção mostrado na Figura 13.5 do texto. O disco tem massa de 200g e raio de 10,0cm . A constante de torção da barra vale 3,00 × 10 - 2Nm . Qual é o período de oscilação d
13.7E Reconsiderando o pêndulo do Exercício 13.6. A) qual é sua energia mecânica se no instante em que o ângulo de torção é θ = 5,00 ° sua velocidade angular é 0,600rad/s ?