Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Pêndulo de Torção

Ver Todos os Exercícios

Teoria

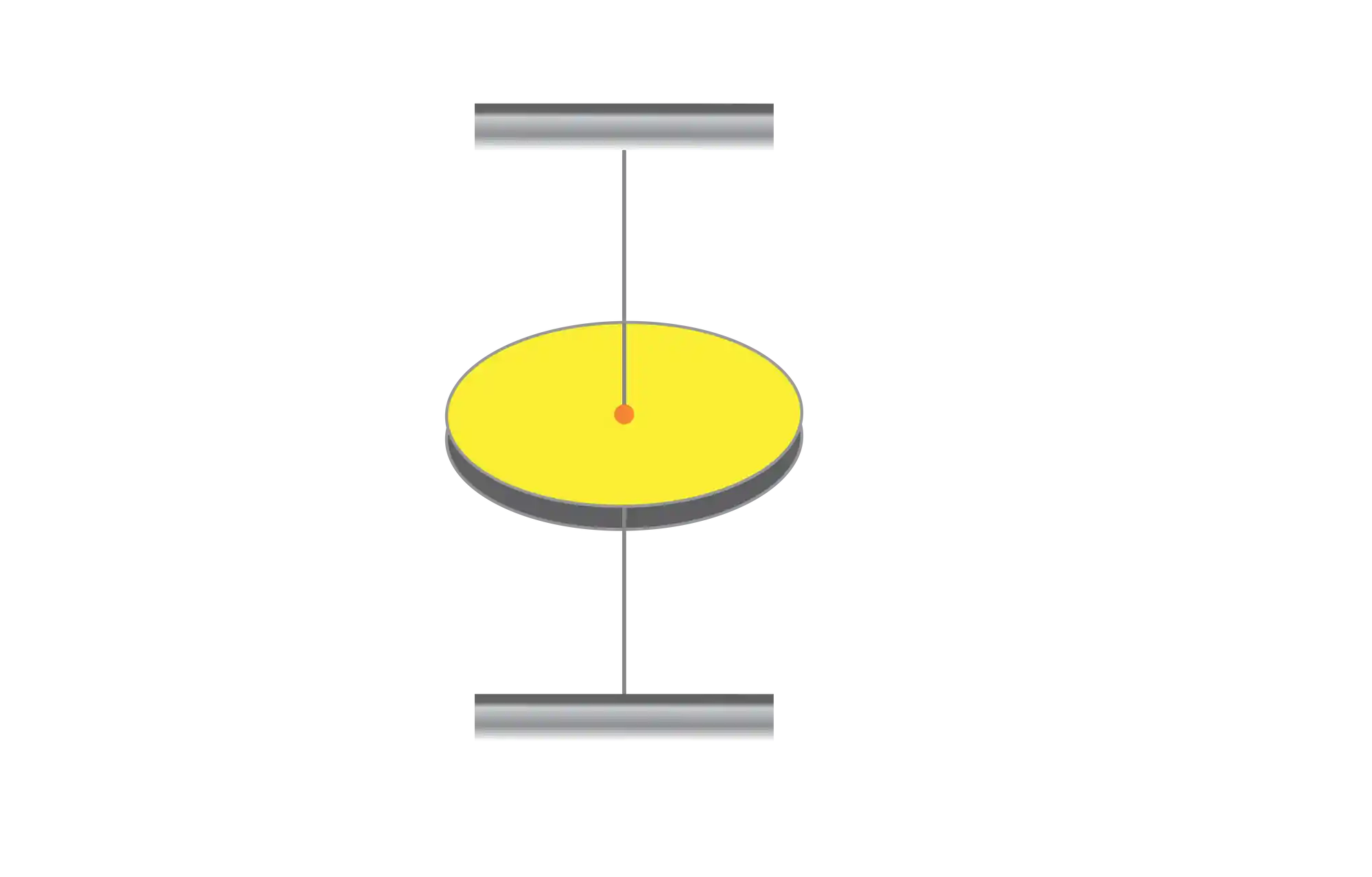
O Pêndulo de Torção realiza oscilações harmônicas se deslocado da sua posição de equilíbrio. Ele é composto por um corpo preso a um fio conectado a um suporte superior e inferior. Assim:

Pêndulo de Torção.
Pêndulo de Torção.

📢 Clique para ver mais:

Como Funciona o Pêndulo de Torção

Pra a gente entender o funcionamento do pêndulo de torção, vamos considerar um disco conectado ao teto por um fio, como vimos acima:

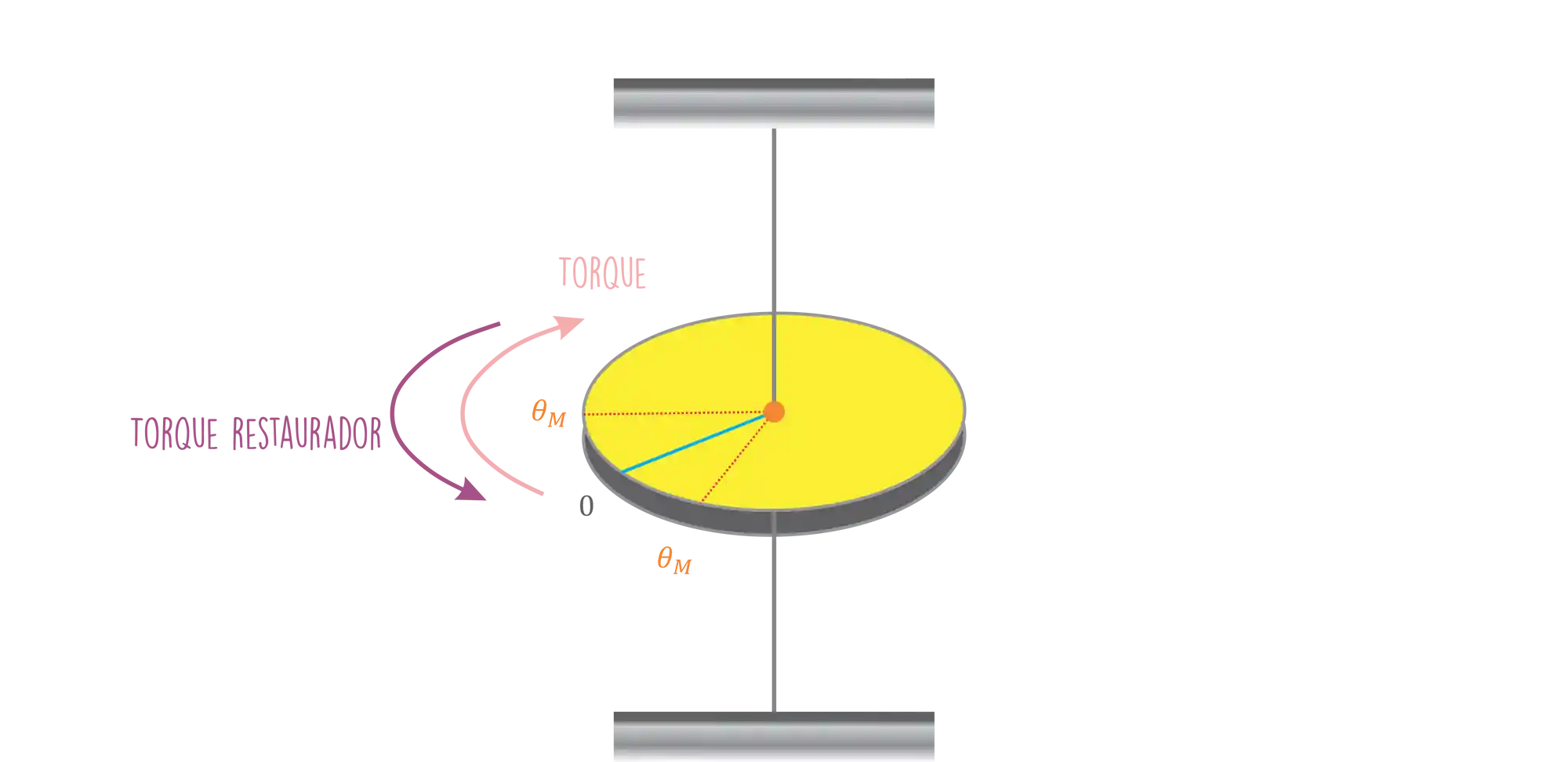
Funcionamento de um Pêndulo de Torção
Funcionamento de um Pêndulo de Torção

Se a gente girar o disco a partir da posição de equilíbrio, , ele vai oscilar entre os ângulos . Para que isso aconteça, deve haver um torque restaurador atuando sobre o disco. Esse torque é dado por:

Onde é a constante de torção. Como só há esse torque agindo sobre o disco, ele causa o torque resultante! Usando a segunda lei de Newton para rotações:

Lembrando que , reagrupando:

Como o termo que acompanha a variável de primeira ordem é velocidade angular ao quadrado, ,podemos escrever:

Podemos calcular então o período do pêndulo de torção:

Exemplo: Calcule o Momento de Inércia

Um engenheiro possui um objeto de 10 kg de forma irregular e precisar conhecer o momento de inércia do objeto em relação a um eixo que passa pelo centro de massa. O objeto é preso a um fio esticado cuja orientação é a mesma do eixo. O fio possui uma constante de torção igual a k=0,50 N⋅mk=0,50 N·m. Se este pêndulo de torção sofre 20 oscilações completas em 50 segundos, qual é o momento de inércia do objeto?

A resolução desse exemplo você pode acompanhar no vídeo abaixo:

Agora vamos praticar com exercícios?

Exemplo: Calcule o Momento de Inércia

Exercícios Resolvidos

Exercício Resolvido #1

Halliday e Resnick, Fundamentos de Física, Volume 2, 8ª edição, Cap 15, pp 108-38

Uma esfera maciça com uma massa de 95   k g e 15   c m de raio está suspensa por um fio vertical. Um torque de 0,23 N .   m é necessário para fazer a esfera girar 0,85   r a d   e manter essa orientação. Qual é o período das oscilações que ocorrem quando a esfera é liberada?

Dados:

Momento de inércia de uma esfera sólida: I = 2 5 m R 2

Passo 1

A fórmula que queremos usar é:

T = 2 π I k

Então precisamos achar o k e o I , certo?

Passo 2

Achar o k é fácil, já que temos o ângulo em que ocorreu o giro e o torque resultante.

Basta a gente usar:

τ = - k θ

Como estamos procurando k , uma constante positiva, vamos usar apenas o módulo da equação acima:

τ = k θ → k = τ θ = 0,23 0,85 = 0,27

Passo 3

Agora vamos calcular o momento de inércia da esfera. Nesse caso, basta a gente aplicar a fórmula:

I = 2 5 m R 2 = 2 5 . 95 . 15.10 - 2 2 = 0,855   k g . m 2

Passo 4

Agora sim podemos calcular o período:

T = 2 π I k

T = 2 π 0,855 0,27 = 11,18   s

Resposta

11,18   s

Exercício Resolvido #2

Halliday e Resnick, Fundamentos de Física, Volume 2, 8ª edição, Cap 15, pp 111-73

Um disco plano circular uniforme possui uma massa de 3,00   k g e um raio de 70,0   c m e está suspenso em um plano horizontal por um fio vertical preso ao centro. Se o disco sofre uma rotação de   2,50   r a d em torno do fio, é necessário um torque de 0,0600   N . m · para manter essa orientação. Calcule

(a) o momento de inércia do disco em relação ao fio.

(b) a constante de torção.

(c) a frequência angular desse pêndulo de torção quando é posto para oscilar.

Momento de inércia de um disco: I = m R 2 2

Passo 1

a)

Vamos apenas aplicar a fórmula do momento de inércia nessa aqui, já que o disco gira ao redor de seu centro de massa:

I = 3 . 70.10 - 2 2 2 = 0,735   k g . m 2

Passo 2

b)

Aqui basta a gente aplicar a fórmula:

τ = - k θ

Em módulo:

k = τ θ = 0,06 2,5 = 0,024

Passo 3

Agora é só a gente usar:

T = 2 π I k

∴

T = 2 π 0,735 0,024 =   34,77   s

Assim:

ω = 2 π T = 0,181   r a d / s

Resposta

a)

I = 0,735   k g . m 2

b)

k = 0,024

c)

ω = 0,181 r a d / s

Exercício Resolvido #3

Uma empresa fabricante de relógios constatou que a roda de balanço de um relógio possui um período de 0 , 50   s . Essa roda de balanço é construída de forma que sua massa fica concentrada em um aro de raio 0 , 3   c m .

Qual é a constante de torção da mola acoplada? Dado I a r o = m R 2 .

  1. k = 2 π m 2 ∙ 10 - 4   N / r a d
  2. k = 144 π 2 m ∙ 10 - 6   N / r a d
  3. k = 1 , 6 π 2 m ∙ 10 - 4   N / r a d
  4. k = 2 m ∙ 10 - 5   N / r a d
  5. k = 1 4 π m ∙ 10 - 5   N / r a d

Passo 1

Bom, galera, como é um aro que vai oscilar, trata-se de um pêndulo de torção. Pela nossa teoria, nós vimos que o período de um pêndulo de torção é dado por:

T = 2 π I k

Onde k é a constante de torção.

Passo 2

Vamos calcular o momento de inércia do aro. A massa é desconhecida, mas o raio é conhecido e vale 0 , 3 c m . Logo:

I = m R 2 = m 0 , 3 ∙ 10 - 2 2 = 9 m ∙ 10 - 6

Passo 3

Agora vamos isolar k na equação do período:

T 2 = 4 π 2 . I k   → k = 4 π 2 I T 2

Substituindo os valores:

k = 4 π 2 ∙ 9 m ∙ 10 - 6 0,5 2 = 36 π 2 m ∙ 10 - 6 1 / 4 = 144 π 2 m ∙ 10 - 6 N / r a d

Resposta

b)

Exercício Resolvido #4

Halliday e Resnick, Fundamentos de Física, Volume 2, 8ª edição, Cap 15, pp 112-93

Um engenheiro possui um objeto de 10 kg de forma irregular e precisar conhecer o momento de inércia do objeto em relação a um eixo que passa pelo centro de massa. O objeto é preso a um fio esticado cuja orientação é a mesma do eixo. O fio possui uma constante torção k = 0,50   N · m .

Se este pêndulo de torção sofre 20   oscilações completas em 50   s , qual é o momento de inércia do objeto?

Passo 1

Se o pêndulo faz 20 oscilações em 50 s , em quantos segundos ele faz uma oscilação?

Basta a gente fazer a divisão:

50 20 = 2,5   s / o s c i l a ç ã o

Ou seja, o período é:

T = 2,5   s

Passo 2

Agora vamos usar a equação:

T = 2 π I k

Queremos achar I , certo? Vamos manipular a equação acima pra achar I :

T 2 = 4 π 2 . I k

∴

I = T 2 . k 4 π 2 = 2,5 2 . 0,5 4 π 2 = 0,079   k g . m 2

Pronto (:

Resposta

I = 0,079   k g . m 2

Exercício Resolvido #5

Uma roda pode girar livremente em torno do seu eixo fixo. Uma mola de constante k é presa a um dos raios a uma distância R do eixo. Suponha que a roda é um anel de massa m e raio R, cujo momento de inércia é igual a I = m R 2 .

a) Calcule a frequência angular ω das pequenas oscilações desse sistema, em termos de m, R, r e k.

b) Suponha que o deslocamento angular máximo de um ponto do anel seja θ 0 e que tem t = 0 s o deslocamento angular desse ponto seja metade desse valor. Escreva a equação do movimento angular do anel.

c) Se o anel tem uma massa m = 3 kg, a constante da mola é k = 100 N/m, θ 0 = 0,01 rad e r   =   R / 2 , calcule a velocidade angular de um ponto do anel em t = 0 s.

Passo 1

a) Vou considerar que a roda gira um ângulo θ em torno do eixo fixo. Para pequenos valores de θ , podemos dizer que a elongação x da mola é:

x = r θ

Escrevendo a segunda lei de Newton para rotações:

τ = I ∂ 2 θ ∂ t 2 = - F r = - k x r = - k r 2 θ

I ∂ 2 θ ∂ t 2 + k r 2 θ = 0

∂ 2 θ ∂ t 2 + k r 2 θ I = 0

∂ 2 θ ∂ t 2 + k r 2 θ m R 2 = 0

Comparando com a equação do MHS:

∂ 2 θ ∂ t 2 + ω 2 θ = 0

Tiramos que:

ω 2 = k r 2 m R 2

ω = r R k / m

Passo 2

b) A equação do movimento do anel vai ser da forma:

θ t = θ 0 cos ⁡ ( ω t + φ )

O problema disse que:

θ 0 = θ 0 cos ⁡ ( φ ) = θ 0 2

cos ⁡ ( φ ) = 1 2

φ = π 3 ,   φ = - π 3

Então:

θ t = θ 0 cos ⁡ r R k m t ∓ π 3

Passo 3

c) A velocidade angular vai ser:

ω t = d θ d t = - ω θ 0 sin ⁡ ω t ∓ π 3

ω 0 = - 0,01 ∙ 1 2 100 3 ∙ sin ⁡ ∓ π 3

ω 0 = - 0,01 ∙ 1 2 100 3 ∙ ∓ 3 2

Fazendo algumas continhas achamos:

ω 0 = ± 0,025   r a d / s

Resposta

a) ω = r R k / m

b) θ t = θ 0 cos ⁡ r R k m t ∓ π 3

c) ω 0 = ± 0,025   r a d / s

Exercícios de Livros Relacionados

O balanço de um relógio antigo oscila com uma amplitude angular de πrad e um período de 0,500 s . Determine (a) a velocidade angular máxima do balanço, (b) a velocidade angular no instante em que o de
35. Um relógio da quatro tiques a cada segundo; cada tique corresponde à metade do período. A roda catarina do relógio consiste em uma fina camada circular com raio de 0,55c m conectada ao conjunto da
52.Um macaco mecânico de 1,80k g é suspenso por um pivô localizado a uma distância de 0,250m de seu centro de massa e começa a oscilar como um pêndulo físico. O período da oscilação com ângulo pequeno
13.6E Considere o pêndulo de torção mostrado na Figura 13.5 do texto. O disco tem massa de 200g e raio de 10,0cm . A constante de torção da barra vale 3,00 × 10 - 2Nm . Qual é o período de oscilação d
13.7E Reconsiderando o pêndulo do Exercício 13.6. A) qual é sua energia mecânica se no instante em que o ângulo de torção é θ = 5,00 ° sua velocidade angular é 0,600rad/s ?